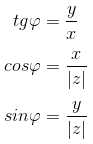Построить радиус вектора z 2 3i

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №39. Геометрическая интерпретация комплексного числа.

Перечень вопросов, рассматриваемых в теме

1. изображение комплексного числа на плоскости- точками;
2. изображение комплексного числа на плоскости- векторами;

3) определение модуля комплексного числа.

Глоссарий по теме:

а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M (a; b)

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Геометрическое изображение комплексных чисел.

а) Комплексные числа изображаются точками плоскости по следующему правилу: a + bi = M (a; b) (рис.1).

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).

Пример. Постройте точки, изображающие комплексные числа: 1; — i; — 1 + i; 2 – 3i (рис.3).

Модуль комплексного числа

Как отмечалось выше, комплексное число также можно изображать радиус-вектором (рис. 4).

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Иногда еще модуль комплексного числа обозначается как r или ρ.

Разбор решения заданий тренировочного модуля

№1. Тип задания: единичный выбор

Найдите модуль комплексного числа z=5-3i

1. 
2. 
3. 4
4. 5

Решим данное задание, используя определение модуля.

Т.к. Re z=5, Im z= -3, то искомое значение

Верный ответ: 2.

№2. Тип задания: рисование.

Изобразите вектором на комплексной плоскости точку z=2+3i

Разобьем z=2+3i на две части: z₁=2 и z₂= 3i. Отметим на плоскости точки О и А, соединим их:

Видео:Радиус векторСкачать

Калькулятор комплексных чисел. Вычисление выражений с комплексными числами

Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.

Калькулятор комплексных чисел

Видео:Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Как пользоваться калькулятором

1. Введите в поле ввода выражение с комплексными числами
2. Укажите, требуется ли вывод решения переключателем «С решением»
3. Нажмите на кнопку «Построить»

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Ввод комплексных чисел

комплексные числа можно вводить в следующих трёх форматах:

• Только действительная часть: 2, 2.5, -6.7, 12.25
• Только мнимая часть: i, -i, 2i, -5i, 2.16i, -12.5i
• Действительная и мнимая части: 2+i, -5+15i, -7+2.5i, -6+i
• Математические константы: π, e

Видео:Как построить точки в системе координат OXYZСкачать

Поддерживаемые операции и математические функции

• Арифметические операции: +, -, *, /, ^
• Получение абсолютного значения числа: abs
• Базовые математические функции: exp, ln, sqrt
• Получение действительной и мнимой частей: re, im
• Тригонометрические функции: sin, cos, tg, ctg
• Гиперболические функции: sh, ch, th, cth
• Обратные тригонометрические функции: arcsin, arccos, arctg, arcctg
• Обратные гиперболические функции: arsh, arch, arth, arcth

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Примеры корректных выражений

• (2+3i)*(5-7i)
• sh(i)
• (4+i) / (3 — 4i)
• sqrt(2i)
• (-3+4i)*2i / exp(2i + (15 — 8i)/4 — 3.75)

Видео:Координаты вектора. 9 класс.Скачать

Комплексные числа

Комплексные числа — это числа вида x+iy , где x , y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i 2 = -1 ).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.

Видео:Радиус-векторыСкачать

Примеры комплексных чисел

• 4+3i — действительная часть = 4, мнимая = 3
• -2+i — действительная часть = -2, мнимая = 1
• i — действительная часть = 0, мнимая = 1
• -i — действительная часть = 0, мнимая = -1
• 10 — действительная часть = 10, мнимая = 0

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi 2 = (ac — bd) + (bc + ad)i
• деление:

Примеры

Найти сумму чисел 5+7i и 5.5-2i :
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом: 5+7i + 5.5-2i = 10.5 + 5i

Найти разность чисел 12-i и -2i :
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом: 12-i — (-2i) = 12 + i

Найти произведение чисел 2+3i и 5-7i :
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом: 2+3i * (5-7i) = 31 + i

Найти отношение чисел 75-50i и 3+4i :
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом: 75-50i / (3+4i) = 1 — 18i

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа: Re(z) = a
• Получение мнимой части числа: Im(z) = b
• Модуль числа: |z| = √(a 2 + b 2 )
• Аргумент числа: arg z = arctg(b / a)
• Экспонента: e z = e a ·cos(b) + i·e a ·sin(b)
• Логарифм: Ln(z) = ln |z| + i·arg(z)
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(4 2 + (-3) 2 ) = √25 = 5

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Формы представления комплексных чисел

Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

• Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: x+iy , где x — действительная часть, а y — мнимая часть
• Тригонометричкая форма — запись вида r·(cos φ + isin φ) , где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
• Показательная форма — запись вида r·e iφ , где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))

Пример:

Переведите число 1+i в тригонометрическую и показательную формы:

• Найдём радиус (модуль) комплексного числа r: r = √(1 2 + 1 2 ) = √2
• Найдём аргумент числа: φ = arctan(

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Аргумент и модуль комплексного числа

Вычислить аргумент и модуль комплексного числа.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ

Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ

Из определения следуют следующие формулы:

Для числа z = 0 аргумент не определен.

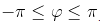
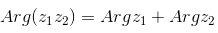Главным значением аргумента называется такое значение &#966, что . Обозначается: arg(z).

	— аргумент от произведения двух комплексных чисел равен сумме аргументов этих чисел
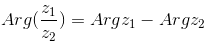	— аргумент частного двух комплексных чисел равен разности аргументов этих чисел
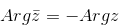	— аргумент от сопряженного комплексного числа равен отрицательному значению аргумента от этого числа.

Модулем комплексного числа z = x + iy называется вещественное число |z| равное:

💡 Видео

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Координаты точки и координаты вектора 1.Скачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

ЕГЭ по Физике 2022. Кинематика. Радиус-векторСкачать

КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ решение задачСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Изобразить область на комплексной плоскостиСкачать

№776. Начертите два неколлинеарных вектора х и у и постройте векторы: a) x+2y; б) ½y + х; в) 3x+½yСкачать

Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать