Построить параллелепипед abcda1b1c1d1 и найти пары 1 параллельные прямые к ab (6 видео)

Практическая работа №5 по теме «Параллельность прямых и плоскостей» для студентов 1 курса

Содержание

«Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
Прямоугольный параллелепипед. Что это такое?
Определение параллелепипеда
Свойства параллелепипеда
Прямой параллелепипед
Прямоугольный параллелепипед
Свойства прямоугольного параллелепипеда
Диагонали прямоугольного параллелепипеда: теорема
Куб: определение, свойства и формулы
Решение задач
Самопроверка
Прямоугольный параллелепипед (продолжение)
📸 Видео

Видео:№79. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью АВС1;Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Практическая работа №5

Тема: «Параллельность прямых и плоскостей».

— формирование логического мышления, пространственного воображения через решение задач;

— развить умение составлять наглядные рисунки для задач;

— воспитывать самостоятельные навыки.

1. Ответить на контрольные вопросы:

1). Записать признак параллельности прямой и плоскости (с рисунком).

2). Записать признак скрещивающихся прямых (с рисунком).

3). Записать признак параллельности плоскостей (с рисунком).

2. Выполнить контрольное задание.

Образец выполнения заданий.

1) параллельные прямые к АВ; 2) скрещивающиеся прямые к ВС.

Решение:

2. Точка М лежит на середине ребра AD тетраэдра DABC . Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно основанию АВС.

Решение:

Т.к. секущая плоскость проходит параллельно основанию => отрезки параллельных плоскостей будут параллельны по свойству параллельности плоскостей ( 1°. Если 2-е параллельные плоскости пересечены третьей, то линии их пересечения будут параллельны).

1. Построим через т. М, MN ǁАВ.

2. Построим через т. N , NK ǁВС.

3. Соединим МК по 2*.

4. MNK — искомое сечение.

3. Средняя линия трапеции лежит в плоскости α. Докажите, что основания трапеции параллельны плоскости α.

MN — средняя линия трапеции, MN ⊂ α.

Доказать: ВСǁα, AD ǁα.

Доказательство:

Т.к. MN — средняя линия трапеции, то по свойству средней линии MN ǁ AD , MN ǁВС =>

ВСǁα, AD ǁα по признаку параллельности прямой и плоскости ( Признак ( — ти прямой и плоскости): Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости).

4. Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба. Докажите, что m и АС — скрещивающиеся прямые.

Доказательство:

Т.к. прямая m ǁ BD => m ǁ ABCD по признаку параллельности прямой и плоскости. По определению параллельных прямых m и BD лежат в одной плоскости, а т.к. АС BD в точке не лежащей на прямой m , то по признаку скрещивающихся прямых, m ∸АС ( Признак (∸ прямых): Если одна из 2-х прямых лежит в некоторой плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся).

S ABC — тетраэдр

Точки M , N и K — середины ребер DA , DB и DC .

Доказать: MNK ǁ ABCD .

Т.к. точки M , N и K — середины ребер DA , DB и DC => MN , NK и MK — средние линии Δ DAB , Δ DBC и Δ ADC соответственно. По свойству средней линии треугольника MN ǁ AB , NK ǁ BC и MK ǁ AC . По признаку параллельности плоскостей, MNK ǁ ABCD ( Признак (ǁ — ти плоскостей) : Если две пересекающиеся прямые одной плоскости, соответственно параллельны двум пересекающимся другой плоскости, то эти плоскости параллельны).

1. Построить параллелепипед ABCDA ₁ B ₁ C ₁ D ₁ и найти пары:

1) параллельные прямые к А D ;

2) скрещивающиеся прямые к A В.

1. Построить параллелепипед ABCDA ₁ B ₁ C ₁ D ₁ и найти пары:

1) параллельные прямые к C ₁ D ₁ ;

2) скрещивающиеся прямые к A ₁ D ₁ .

2. Точка М лежит на середине ребра AD тетраэдра DABC . Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно плоскости В D С.

2. Точка М лежит на середине ребра D С тетраэдра DABC . Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно плоскости А D В.

3. Точка М плоскости параллелограмма ABCD . Доказать, что CD ABM .

3. т. A α и т. B α, а точка С α. Докажите, что прямая проходящая через середины AC и BC -на плоскости α.

4. Даны параллелограмм ABCD и трапеция ABEK с основанием EK , не лежащие в одной плоскости. Докажите, что AD ∸ EK .

4. Дан параллелограмм ABCD м точка S ∉ ABCD . Точки M и N — середины SB и SC . Доказать, что MN ∸ CD .

5. Дан параллелепипед ABCDA ₁ B ₁ C ₁ D ₁ . Точки K , L , M и N середины сторон AD , BC , B ₁ C ₁ и A ₁ D ₁ соответственно. Докажите плоскость KLMNǁABB ₁ A ₁ .

5. Дана четырехугольная пирамида S ABCD .

Точки K , L , M и N — середины ребер SA , SB , SC и SD соответственно. Доказать, что плоскость KLMN ǁ ABCD .

Видео:№114. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте на ребре АВ точку М. Постройте сечение паралСкачать

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Видео:№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

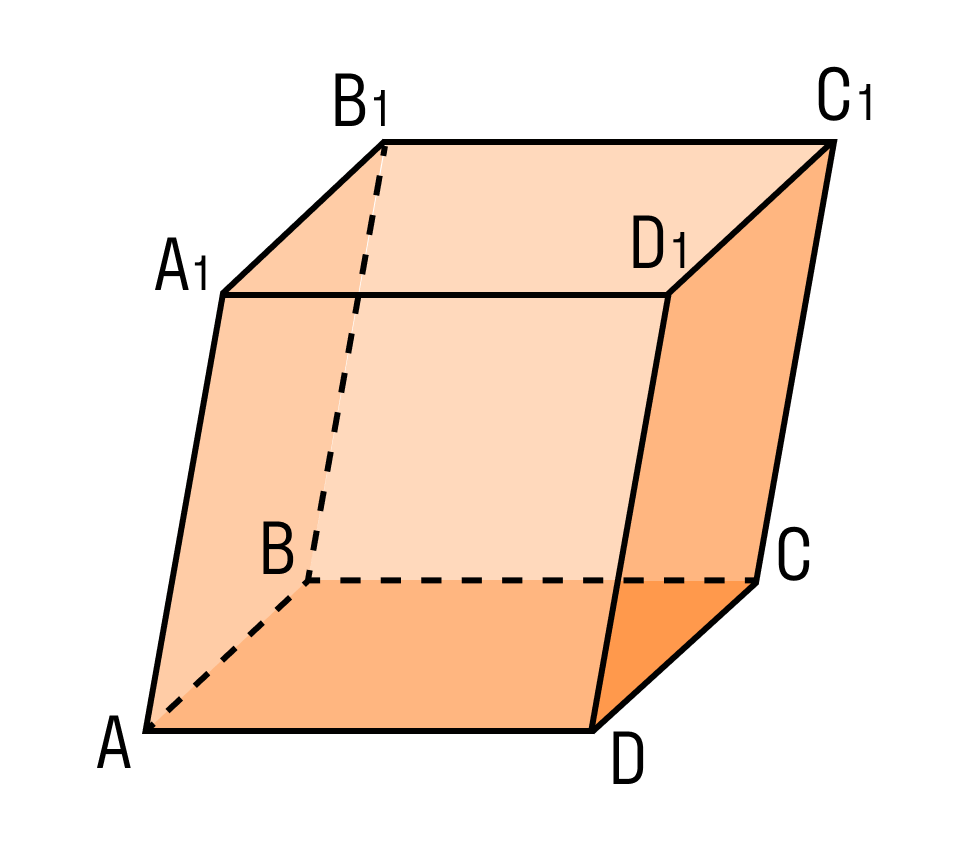
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Противолежащие грани параллелепипеда равны и параллельны друг другу.
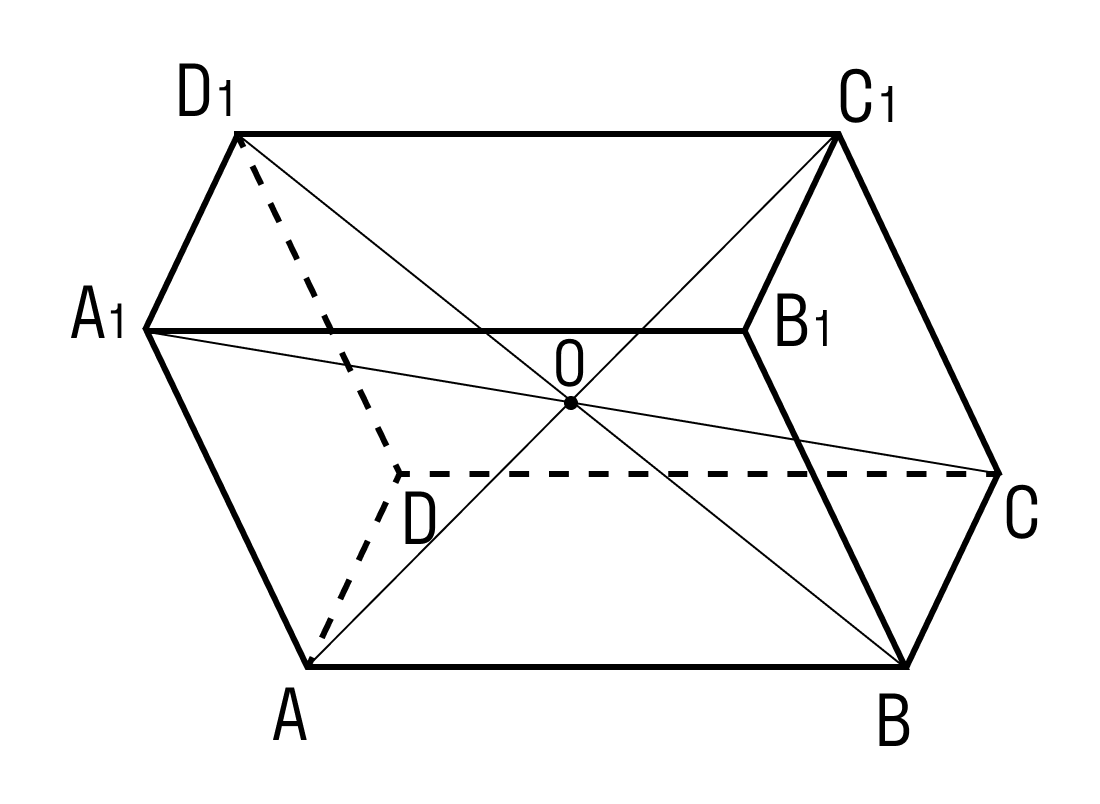
Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Параллелепипед симметричен относительно середины его диагонали.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Видео:Как строить сечения параллелепипедаСкачать

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
Высота прямого параллелепипеда равна длине бокового ребра.
Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота
Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания
Объем прямого параллелепипеда
V = Sо*h

Видео:№84. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящейСкачать

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

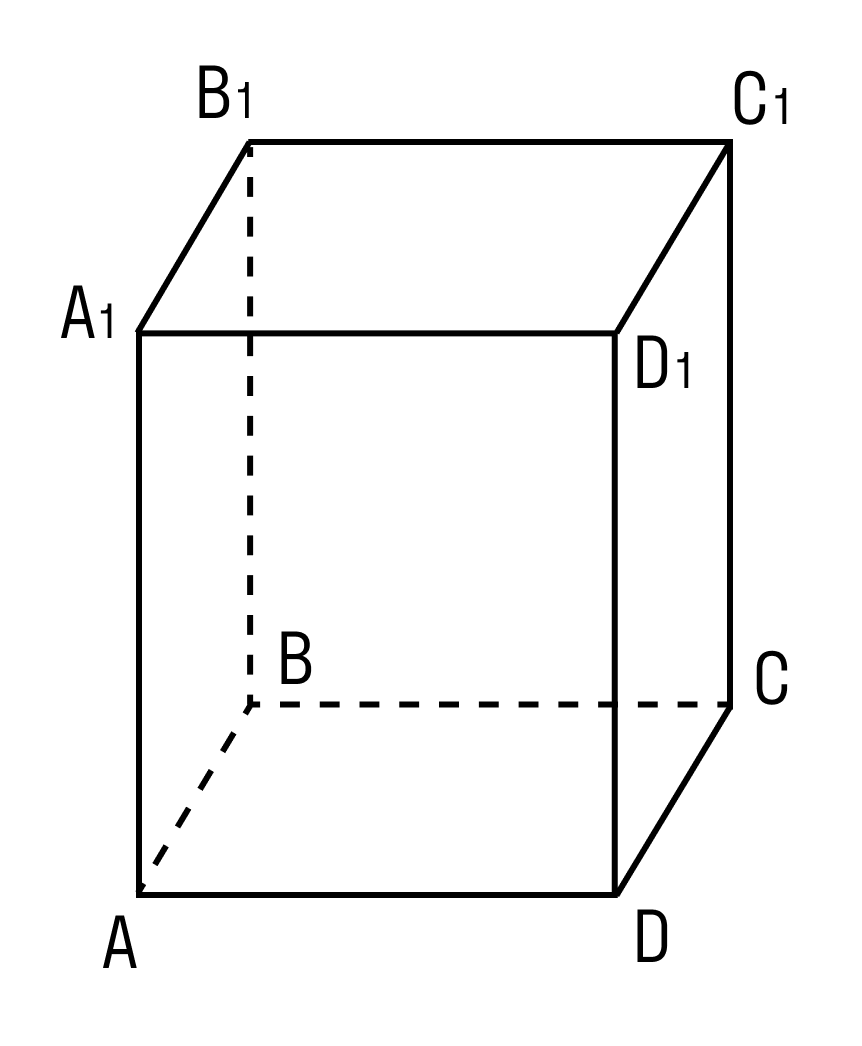
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Видео:№116. Дан параллелепипед ABCDA1B1C1D1. Докажите, что: а) DC⊥B1C1, и AB⊥A1DСкачать

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
Противолежащие грани параллелепипеда попарно параллельны и равны.
Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
Диагонали прямоугольного параллелепипеда равны.
В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
Любая грань прямоугольного параллелепипеда может быть принята за основание.
Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота
Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро
Площадь поверхности
Sп.п = 2(ab+bc+ac)

Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

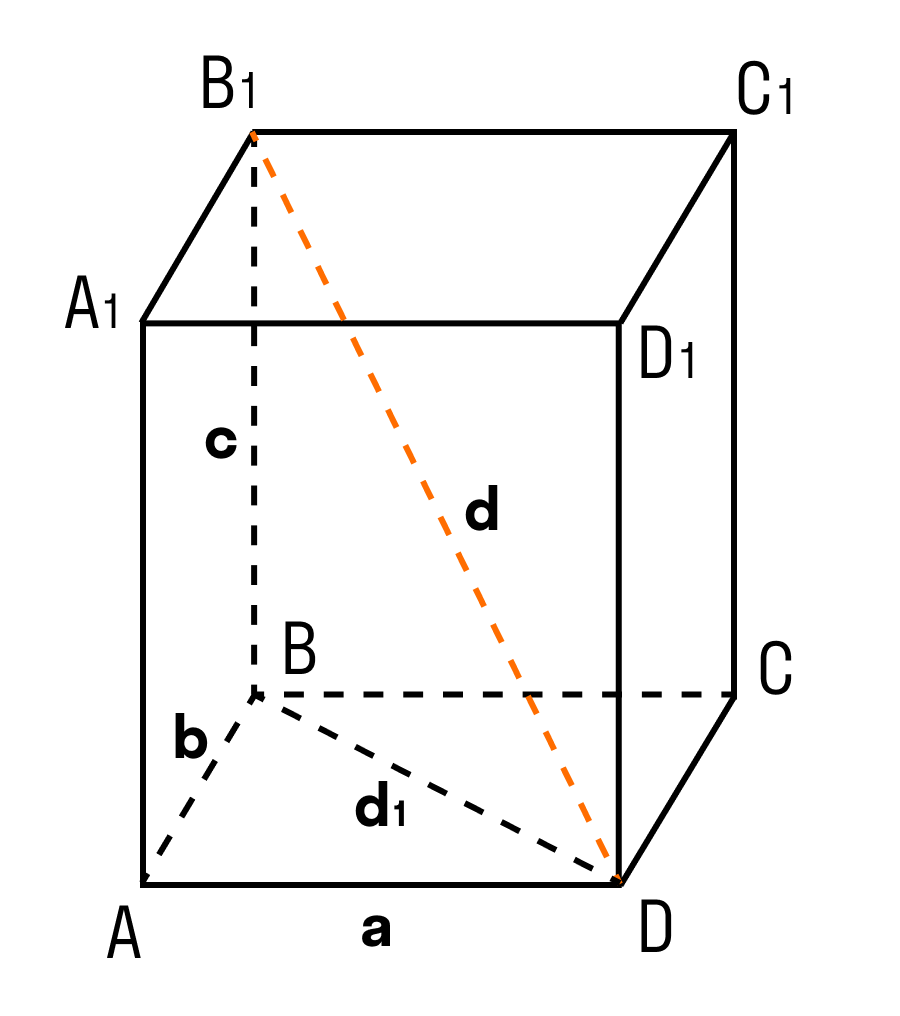
Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Видео:№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

В кубе 6 граней, каждая грань куба — квадрат.
Противолежащие грани параллельны друг другу.
Все углы куба, образованные двумя гранями, равны 90°.
У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
Диагонали куба равны.
Диагональ куба в √3 раз больше его ребра.
Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Объем куба через длину ребра a
V = a3
Площадь поверхности куба
S = 6a2
Периметр куба
P = 12a

Видео:№76. Дан параллелепипед ABCDA1B1C1D1. Докажите, что AC||A1C1 и BD||B1D1.Скачать

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

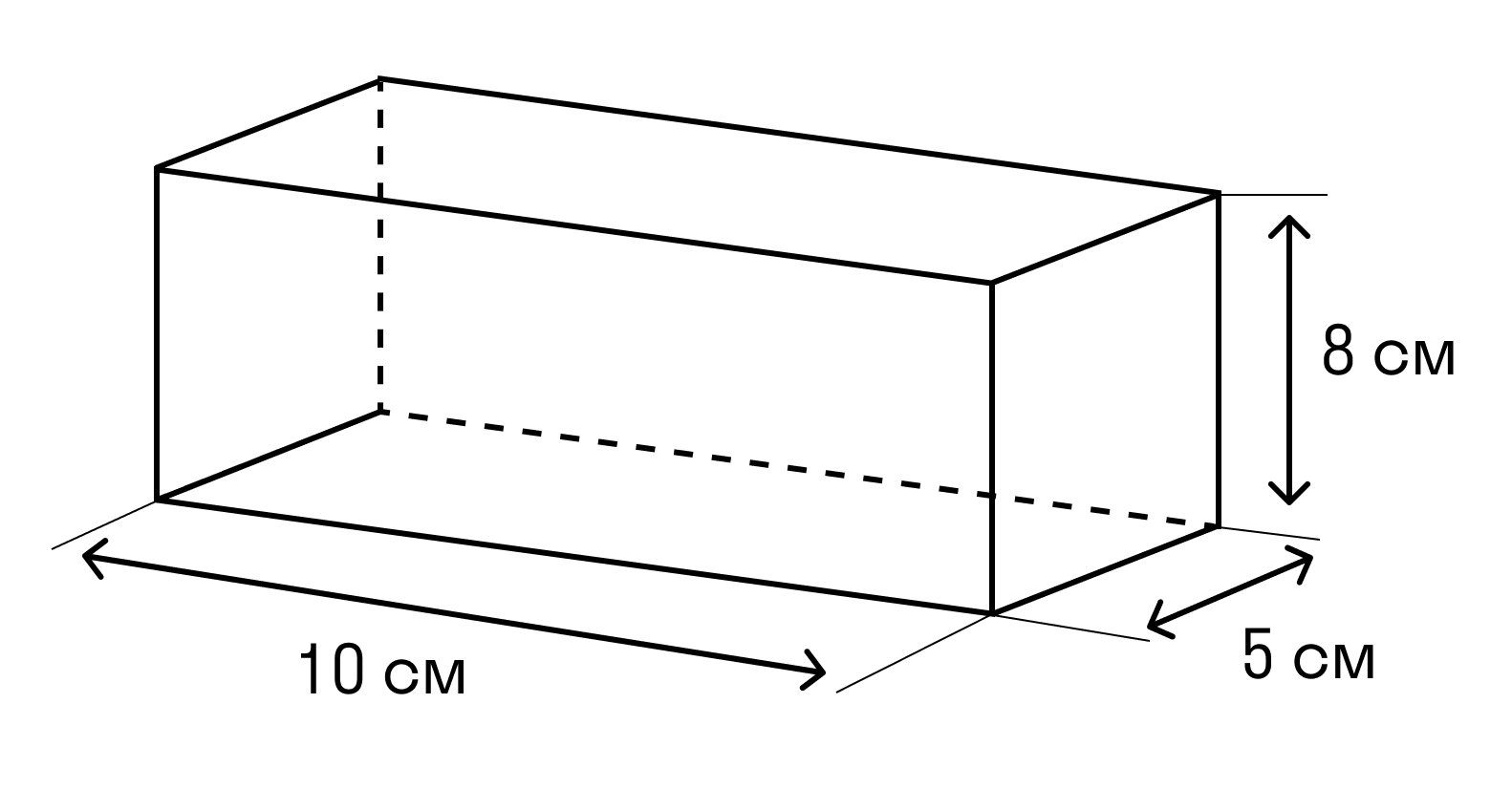
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

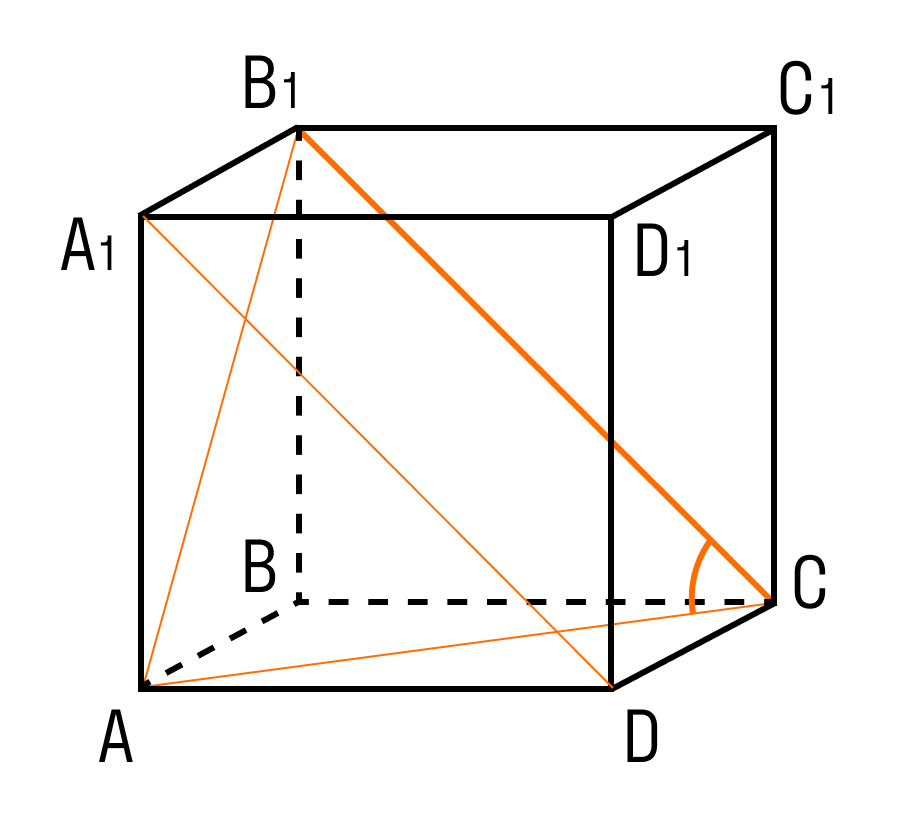
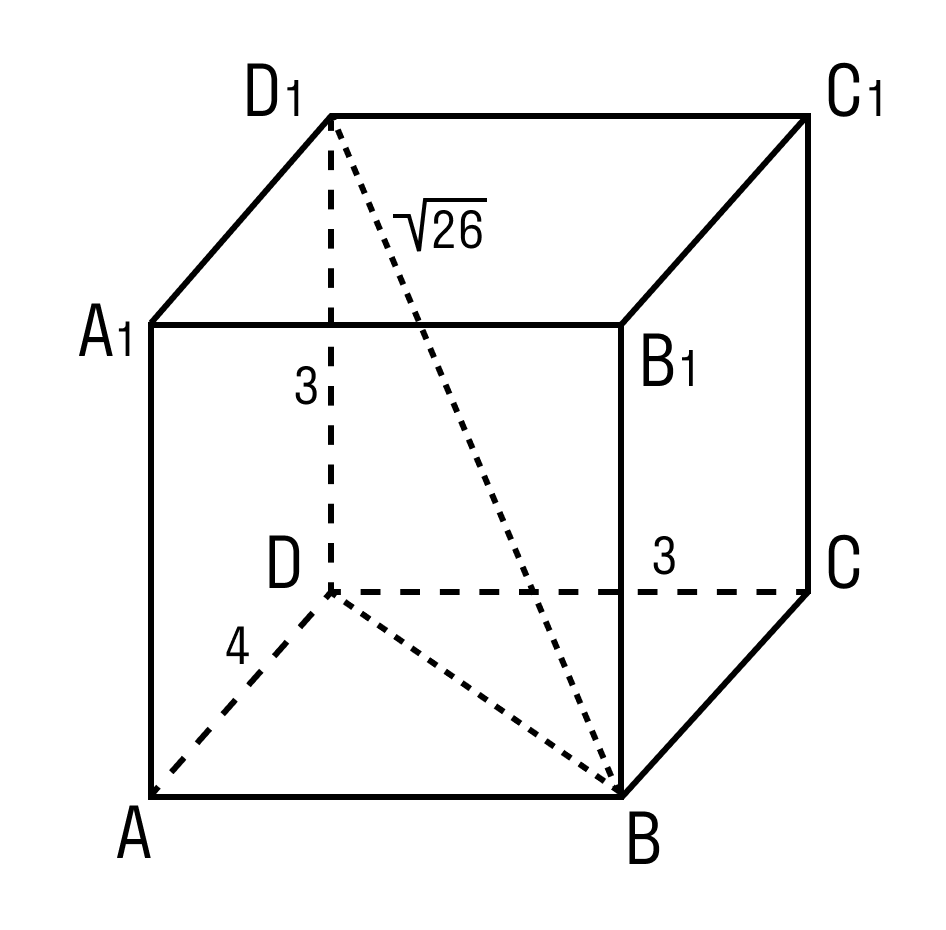
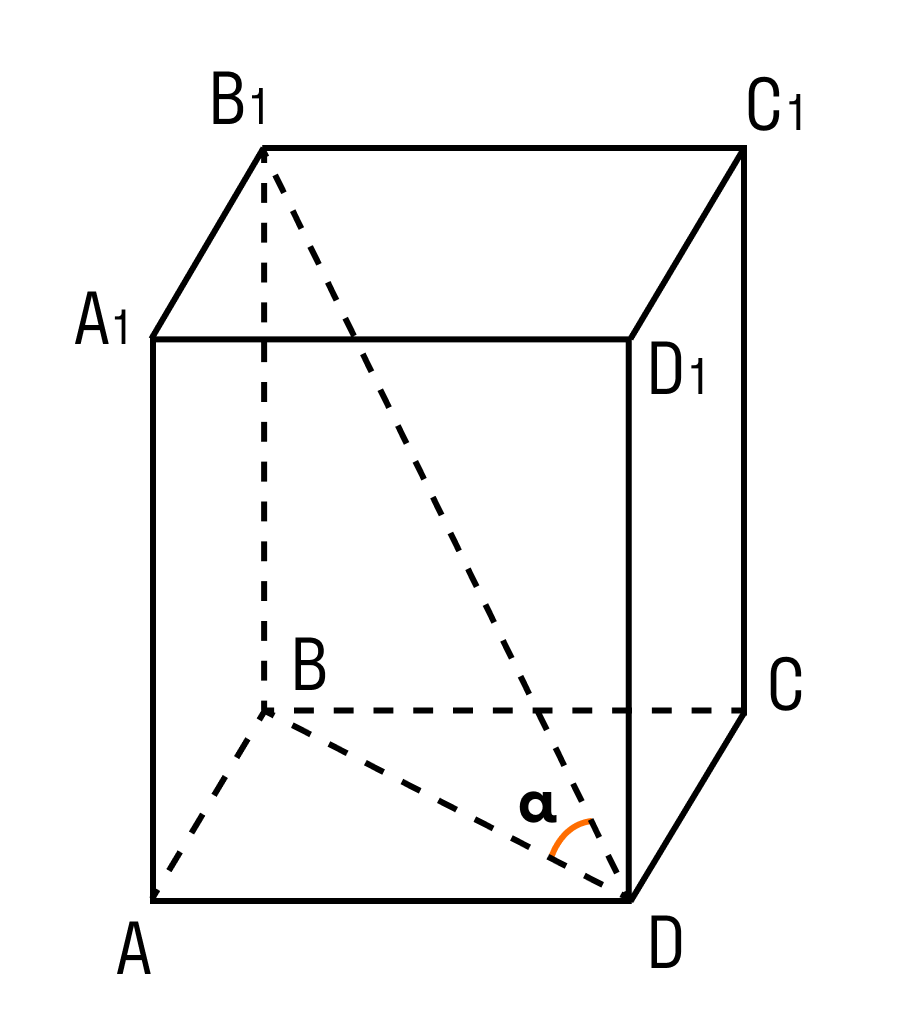
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁ 2 = DD₁ 2 + BD 2
BD 2 = BD₁ 2 – DD₁ 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1
A₁B₁ = AB = 1.

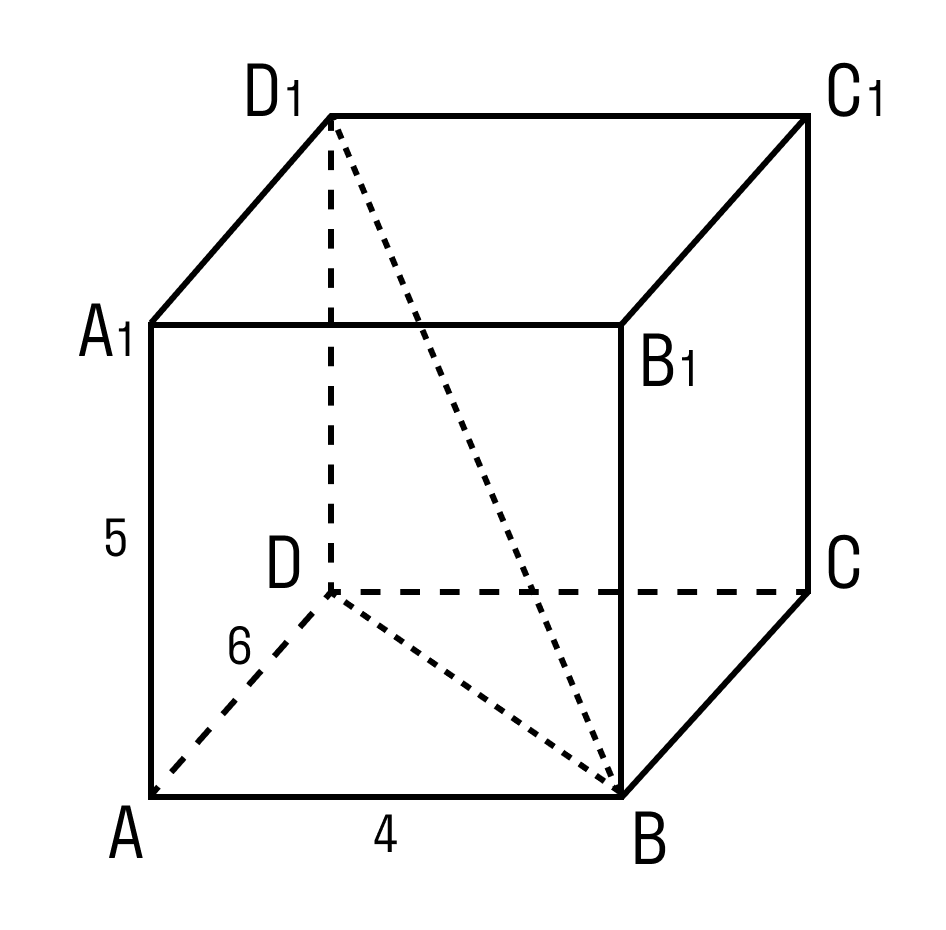
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Видео:№82. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте внутреннюю точку М грани АА1В1ВСкачать

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
основание прямоугольного параллелепипеда — прямоугольник;
три измерения прямоугольного параллелепипеда: длина, ширина, высота;
диагональ параллелепипеда равна сумме квадратов его измерений.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Прямоугольный параллелепипед (продолжение)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок предназначен для самостоятельного ознакомления с темой «Прямоугольный параллелепипед (продолжение)». На этом занятии мы продолжим изучать прямоугольный параллелепипед. Вначале повторим основные свойства этой геометрической фигуры, затем решим несколько задач с использованием этих свойств.