Блок схема вычисляющая длину окружности

Итак, с сегодняшнего дня мы начинаем вести новую рубрику: «Решение задач», в которой будем рассматривать задачи, взятые из сборника М.Э.Абрамяна «1000 ЗАДАЧ ПО ПРОГРАММИРОВАНИЮ».

Открыв задачник и прочитав аннотацию, Вы, скорее всего, озадачитесь тем, что данное пособие предназначено для студентов механико-математического, физического и экономического факультетов, но смею Вас заверить, что это весьма универсальная книга, которая подходит как студентам, так и школьникам. Возможно, задачи из первых разделов книги покажутся Вам простыми — в этом случае используйте наш разбор только для проверки своих решений; но если же по каким-либо причинам решить задачи Вы не в состоянии, то тогда присоединяйтесь к нам.

Begin1. Дана сторона квадрата a. Найти его периметр P = 4·a.

Прежде всего напомню, что для ввода и вывода информации, в Паскале используют следующие операторы:

• Read (Readln) — ввод значений с клавиатуры;
• Write (Writeln) — вывод результата (и вообще чего-либо) на экран.

Блок-схема

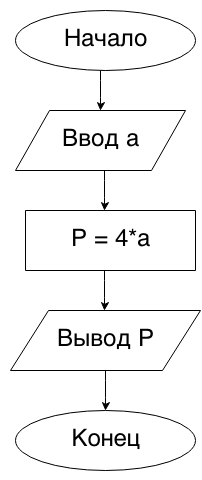
Таким образом, решение задачи становится очевидным.

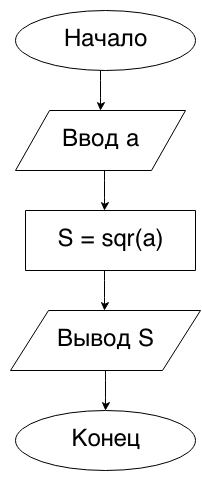
Begin2. Дана сторона квадрата a. Найти его площадь S = a 2 .
При решении данной задачи воспользуемся функцией sqr . Можно, конечно, вычислять квадрат, умножая число само на себя (S=a*a), но при вводе действительно больших чисел наша программа будет выполняться гораздо дольше, нежели при использовании sqr .

Блок-схема

Begin3°. Даны стороны прямоугольника a и b. Найти его площадь S = a·b и периметр P = 2·(a + b).

Да, задача по сути своей проста и подобна предыдущим, поэтому поскорее составим к ней решение и перейдем к следующей.

Блок-схема

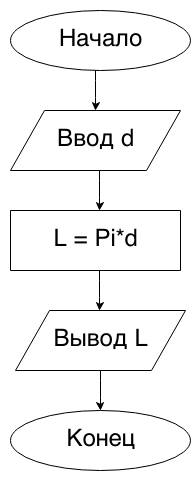
Begin4. Дан диаметр окружности d. Найти ее длину L = π·d. В качестве значения π использовать 3.14.

У вас, наверняка, возникает вопрос π — это константа или переменая? Так как π не изменяется в течение программы, π — константа. Вообще в Паскале уже встроена такая константа, но ее значение:

А так как в условии задачи указано, что в качестве значения π нужно использовать 3.14, то следует объявить π в разделе описания констант.

Блок-схема

Begin5. Дана длина ребра куба a. Найти объем куба V = a 3 и площадь его поверхности S = 6·a 2 .

Для решения задачи используем функцию power(x, a), где a — степень, x — число возводимое в степень (разумеется, использовать ее мы будем только для возведения числа в третью степень, квадрат числа по-прежнему находим с помощью sqr(x) ).

Блок-схема

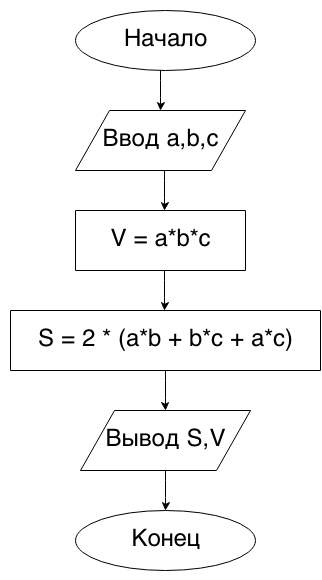
Begin6. Даны длины ребер a, b, c прямоугольного параллелепипеда. Найти его объем V = a·b·c и площадь поверхности S = 2·(a·b + b·c + a·c).

Блок-схема

Begin7°. Найти длину окружности L и площадь круга S заданного радиуса R:
L = 2·π·R, S = π·R 2 .
В качестве значения π использовать 3.14.

Блок-схема

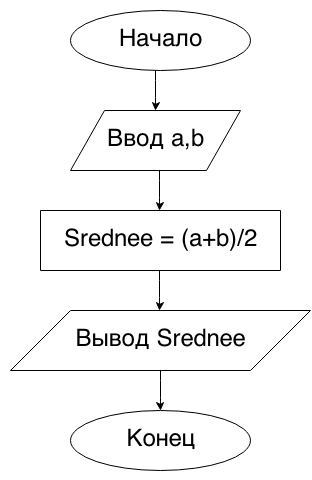
Begin8. Даны два числа a и b. Найти их среднее арифметическое: (a + b)/2.

Блок-схема

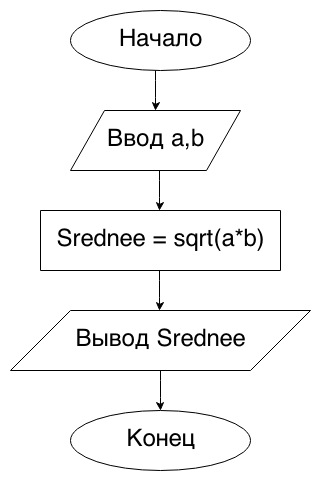
Begin9. Даны два неотрицательных числа a и b. Найти их среднее геометрическое, то есть квадратный корень из их произведения: √(a*b).

Напомню, что для нахождения квадратного корня мы используем функцию sqrt .

Блок-схема

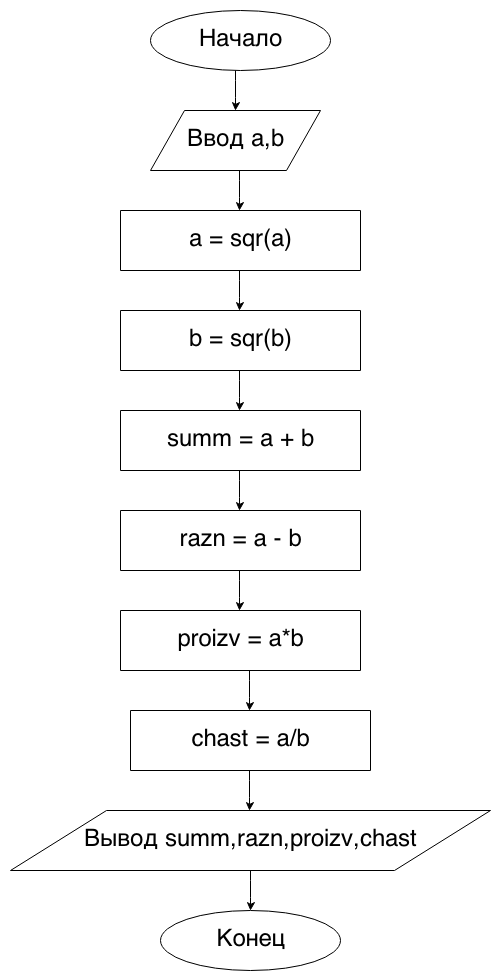
Begin10. Даны два ненулевых числа. Найти сумму, разность, произведение и частное их квадратов.

Блок-схема

Ну вот и все. Следующая публикация с решением задач выйдет в ближайшие дни.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Составить алгоритм вычисления длины окружности и площади круга заданных радиусом R?

Информатика | 10 — 11 классы

Составить алгоритм вычисления длины окружности и площади круга заданных радиусом R.

Формулы : C = 2πR, S = πR²

write (‘vvedite radius : ‘) ;

writeln (‘dlina okruzhnosti = ‘, c : 0 : 5, ‘, ploschad = ‘, s : 0 : 5) ;

Видео:15 Задача: Вычислить площадь и длину окружности круга при помощи PythonСкачать

1. Вычислить длину окружности и площадь круга радиуса — r2?

1. Вычислить длину окружности и площадь круга радиуса — r

Известна длина окружности, найти площадь круга, ограниченной в этой окружности

Найти площадь кольца, внутренний радиус — r1, внешний радиус — r2.

Видео:Длина окружности. Математика 6 класс.Скачать

Вычислить площадь и длину круга по заданному радиусу с клавиатуры?

Вычислить площадь и длину круга по заданному радиусу с клавиатуры.

Видео:Длина окружности. 9 класс.Скачать

Напишите пожалуйста блок — схему для вычисления диаметра и длины окружности и площади круга, если задан R?

Напишите пожалуйста блок — схему для вычисления диаметра и длины окружности и площади круга, если задан R.

Видео:+Как найти длину окружностиСкачать

Составить алгоритм нахождения площади и длины окружности если известен радиус?

Составить алгоритм нахождения площади и длины окружности если известен радиус.

Составить алгоритм нахождения площади и длины окружности если известен диаметр.

Составить в виде блог — схемы.

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Напишите блок — схему для вычисления диаметра и длины окружности и площадь круга, если задан R?

Напишите блок — схему для вычисления диаметра и длины окружности и площадь круга, если задан R.

Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Программирование линейных алгоритмов вычислите длину окружности и площадь круга одного и того же заданного радиуса R?

Программирование линейных алгоритмов вычислите длину окружности и площадь круга одного и того же заданного радиуса R.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Составить программу вычисления площади круга и длину окружности величину радиуса вводить с клавиутуры , выход из программы при нулевом радиусе?

Составить программу вычисления площади круга и длину окружности величину радиуса вводить с клавиутуры , выход из программы при нулевом радиусе.

Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

Найти длину окружности и площадь круга заданного радиуса R?

Найти длину окружности и площадь круга заданного радиуса R.

В качестве значения Pi использовать 3.

Видео:Длина дуги окружности. 9 класс.Скачать

Кто в этом разбирается?

Кто в этом разбирается?

Помогите пожалуйста 1.

Составить линейный алгоритм и программу вычисления периметра прямоугольника, если заданы длины его сторон А и В.

2. Составить алгоритм и программу вычисления произведения и разности двух заданных чисел Р и В.

3. Составить алгоритм и программу вычисления объёма куба, если задана длина его ребра В.

4. Составить алгоритм и программу вычисления площади круга, если задан его радиус.

5. Составить алгоритм и программу вычисления периметра треугольника, если заданы значения его сторон : А, В и С.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Составить программу которая определяет длину окружности и площадь круга одного и того же заданного радиуса R?

Составить программу которая определяет длину окружности и площадь круга одного и того же заданного радиуса R.

Вы перешли к вопросу Составить алгоритм вычисления длины окружности и площади круга заданных радиусом R?. Он относится к категории Информатика, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Информатика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

А) Рыбак или Море или Пушкин б) рыба и (мори или Пушкин) г) Рыбак и (Море или Пушкин или Невод) в) Рыбак и Мори и Пушкин.

1) Разность : получится число переменных данного типа, которые смогли бы поместиться между адресами, на которые указывают указатели. Например : / / зададим фиксированные адреса : int p1 = (int * )0x1000 ; int p2 = (int * )0x1004 ; int e = p2 — p1 ; ..

Современный человек живет, информацией, постоянно выискивая для себя новое и новое, не представляя своё существование без неё. Но информационное изобилие было не всегда. Чем дальше вглубь веков, тем меньше информации, которой пользовался человек, т..

11100100 1000000 101101101.

(I — информационный объем текста, K — кол — во символов, i — вес одного символа / бит на символ) Дано : K = 75 шт i = 16 бит I — ? Решение : I = K * i = 75 * 16 бит = 1200. 0 бит 1200. 0 бит = 150. 0 байт.

8 цветов, на таблице подробно указано.

Я была в лесу летом. Там я собирала грибы. Было много деревьев и травы, кустов. В конце лета листья начинали опадать. Было очень тихо, слышно только пение птиц. Слышно как шуршит под ногами трава и ветки. Воздух свежий. В лесу очень хорошо отд..

Да, установка нелицензионной версии ОС windows xp является в этом случае не законной и нарушает права автора этого пакета(программы). Потому что компания приобрела у представителя компании ОС и установила уже программу ранее. Принцип лицензирования..

Алфавит содержит 8 символов⇒ для записи одного символа требуется log(2)8 = 3 бита. В приведенном сообщении 11 символов. Количество информации в сообщении = 3 * 11 = 33 бита.

Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»
методическая разработка по информатике и икт (9 класс) на тему

Занятие, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Практическая работа на тему

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»

В данной разработке представлены задачи с геометрическим содержанием по теме «Окружность и круг» для 9 класса. Для этих задач разработаны алгоритмы и программы на псевдокоде и языке Паскаль. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе.

Видео:Длина окружности и площадь кругаСкачать

Скачать:

Видео:ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Предварительный просмотр:

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС »

учитель математики информатики

Видео:Окружность и круг, 6 классСкачать

Введение

Одна из главная задач ФГОС, которые призваны реализовать развивающий потенциал общего среднего образования — готовить своих учеников к жизни, обеспечить ребенку общекультурное, личностное и познавательное развитие, вооружить умением учиться. Перед выпускниками, вступающими в самостоятельную жизнь, встаёт проблема решать новые, неизвестные задачи, которые неизбежно встанут перед ними. Результат образования можно «измерить» умением успешно решать такие задачи.

В новых стандартах метапредметным результатам уделено особое внимание, поскольку именно они обеспечивают более качественную подготовку учащихся к самостоятельному решению проблем, с которыми встречается каждый человек на разных этапах своего жизненного пути в условиях быстро меняющегося общества. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе. Программирование обучает методам мышления, общим подходам к постановке и решению задач. Поэтому выбрана тема занятия, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Видео:КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Основная часть

Тема занятия : Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг».

Видео:Блок-схема циклического алгоритма. Вычисление n!Скачать

Задания, которые рассматриваются на занятии:

• вычисление длины окружности по заданному радиусу;
• нахождение площади круга, ограниченного окружностью заданного радиуса;
• нахождение площади кольца по внутреннему и внешнему радиусам;
• вычисление расстояния между двумя точками с заданными координатами;
• найти площади сектора по радиусу и дуге;
• определение минимального радиуса круга, в который попадают точки, заданные координатами на плоскости;

Для решения задач используем линейные структуры, ветвления и циклы.

Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Проверяемые элементы содержания

Формальное исполнение алгоритма, записанного на естественном языке или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд.

Знание основных конструкций языка программирования, понятия переменной, оператора присваивания.

Умение исполнить алгоритм для конкретного исполнителя с фиксированным набором команд.

Анализ алгоритма, содержащего вспомогательные алгоритмы, цикл и ветвление.

Умение анализировать результат исполнения алгоритма.

Видео:Как найти длину окружностиСкачать

Основное содержание теоретической части

Алгоритмы работы с величинами: константы, переменные, понятие типов данных, ввод и вывод данных.

Структура программы на языке Паскаль. Представление данных в программе. Правила записи основных операторов: присваивания, ввода, вывода, ветвления, циклов.

Этапы решения задачи с использованием программирования: постановка задачи, формализация, алгоритмизация, кодирование, отладка, тестирование.

Практика на компьютере: знакомство с системой программирования на языке Паскаль; ввод, трансляция и исполнение данной программы; разработка и исполнение линейных, ветвящихся и циклических программ.

Переменная, константа, операторы ввода/вывода, оператор присваивания, арифметические операции с переменными.

Создание с использованием свойств геометрических фигур математических моделей для решения задач практического характера и задач из смежных дисциплин (для данного занятия – конкретно геометрии), исследовать полученные модели и интерпретировать результат.

Задачи на применение линейных алгоритмических структур. В ходе решения задач повторяются формулы курса геометрии 9 класса: вычисление длины окружности, площади круга, площади кольца, площади сектора, расстояния между двумя точками на плоскости, заданных координатами (метод координат в курсе геометрии).

Видео:Как просто вычислить ДЛИНУ ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА I ГЕОМЕТРИЯ I SkysmartСкачать

Задания на этапе первичного закрепления

Рассмотрим подробно задачи геометрического содержания с постановкой, математической моделью, алгоритмом, программой на языке Паскаль и полученными результатами (скриншот).

Задача 1. Вычислить длину окружности по заданному радиусу.

1. Результат – найти длину окружности.
2. Исходные данные – радиус окружности.
3. Ограничения на результат – положительное число.
4. Ограничения на исходные данные – положительное число.

Математическая модель. Вычислить длину окружности по формуле

Описать переменные. Ввести данные.

Вычислить по формуле длины окружности C= 2*π*R.

Write( ‘Введите радиус окружности R= ‘ );

WriteLn( ‘Длина окружности С= ‘ ,C: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 37, 57344814. Верно.

Задача 2. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

1. Результат – площадь круга.
2. Исходные данные – длина окружности.
3. Ограничения на результат – положительное число.
4. Ограничения на исходные данные – положительное число.

Математическая модель. Выразить радиус R из формулы длины окружности C= 2*π*R. Вычислить радиус R=C/(2* π). Вычислить площадь круга по формуле S= .

Описать переменные. Ввести данные.

Выразить радиус R из формулы длины окружности.

Вычислить радиус по формуле R=C/(2* π). Вычислить площадь круга по формуле S= .

Write( ‘Введите длину окружности С= ‘ );

WriteLn( ‘Площадь круга = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверка результата с помощью калькулятора, получим число 426, 5116724. Значит, программа правильна.

Задача 3. Найти площадь кольца, внутренний радиус которого равен r, а внешний – заданному числу R (R> r).

1. Результат – найти площадь кольца.
2. Исходные данные – внутренний радиус равен r, а внешний – R (R> r).
3. Ограничения на результат – положительное число.
4. Ограничения на исходные данные – положительные числа.

Математическая модель. Найдём площадь кольца по формуле S к =π*(R*R-r*r), где – R — внешний радиус, r-внутренний радиуc, (R> r).

Описать переменные. Ввести данные.

Вычислить по формуле площадь кольца по формуле S к =π*(R*R-r*r).

Writeln( ‘Введите радиусы окружностей R2 и R1 ‘ );

S := pi * (R2 * R2 — R1 * R1);

WriteLn( ‘Площадь кольца S = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 12, 56637061. Верно.

Задача 4. Вычислить расстояние между двумя точками с координатами X1, Y1 и X2, Y2.

1. Результат – найти расстояние R между двумя точками на плоскости.
2. Исходные данные – даны координаты точек (X1, Y1) и (X2, Y2).
3. Ограничения на результат – ограничение на расстояние R>=0
4. Ограничения на исходные данные — ограничений на координаты нет.

Математическая модель. Выведем формулу для вычисления расстояния между двумя точками на плоскости.

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x b — x a ;
BC = y b — y a .

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости: AB = .

Описать переменные. Ввести данные.

Вычислить расстояние между точками по формуле R= .

Напишем алгоритм на псевдокоде

* вывод (‘Введите координаты (x и y) точки 1’)

* вывод (‘Введите координаты (x и y) точки 2’)

* R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

* вывод (‘расстояние между точками 1 и 2 равно ‘, R:10:3);

X1, X2, Y1, Y2, R: Real ;

Writeln( ‘Введите координаты (x и y) точки 1’ );

Writeln( ‘Введите координаты (x и y) точки 2’ );

R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

Write( ‘расстояние между точками 1 и 2 равно ‘ , R: 10 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 4. Верно.

Задача 5. Найти площадь сектора, радиус которого равен 15.4, а дуга содержит заданное число радиан ϕ .

1. Результат – площадь сектора.
2. Исходные данные – величина угла в радианах.
3. Ограничения на результат – положительное число.
4. Ограничения на исходные данные – значение дуги в радианах меньше, чем 2π ≈ 6.28. Иначе сектор будет по величине больше круга.

Модель. Выведем формулу для вычисления площади сектора через угол, выраженный в радианах. Сектор круга ограничивается дугой между двумя точками А и В на окружности и двумя радиусами, проведёнными из концов дуги (точек А и В) к центру круга.

Два радиуса делят всю площадь круга на 2 сектора. Если угол между этими радиусами будет развёрнутым (180 0 ), то эти секторы будут между собой равны. Площадь сектора круга – это часть площади всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число S= . Площадь кругового сектора в радиан (полукруга) равна . Поэтому площадь сектора в один радиан в π раз меньше, т.е. равна : π. Значит, площадь сектора в α радиан равна =

* вывод (‘Введите величину дуги кругового сектора (в радианах)’)

* вывод (‘Площадь кругового сектора =’, S:8:2)

write(‘Введите величину дуги кругового сектора (в радианах) ‘);

writeln(‘Площадь кругового сектора = ‘, S:8:2)

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора.

Задача 6. Даны координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn,yn). Определить минимальный радиус круга, в который попадают все эти точки. Центр круга находится в начале координат.

1. Результат – определить минимальный радиус круга, в который попадают точки с заданными координатами.
2. Исходные данные – координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn, yn).
3. Ограничения на результат – неотрицательное действительное число.
4. Ограничения на исходные данные – координаты точек выражаются действительными числами, количество точек N — натуральное число.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОД: Радиус круга с центром в начале координат вычисляется по формуле R= . Для наглядности рисунок.

АЛГОРИТМ. Вычисляем радиус (расстояние от начала координат до точки) для каждой точки, выбираем минимальное значение. Сравниваем два числа, наименьшее значение записываем как минимум. Это и будет минимальным значением радиуса. Так как количество точек известно, организуем цикл с параметром.