Существует ли такой треугольник

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

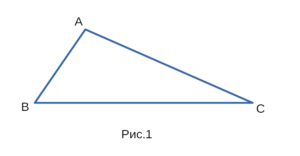
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

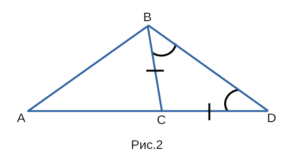
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

1. Проведем отрезок CD равный отрезку CB.
2. △BCD — равнобедренный, значит ∠ CBD=∠CDB.
3. Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB

Видео:№248. Существует ли треугольник со сторонами: а) 1 м, 2 м и 3 м; б) 1,2 дм, 1 дм и 2,4 дм?Скачать

Определить существование треугольника по трем сторонам

У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится.

Пользователь вводит длины трех сторон. Программа должна определять, может ли существовать треугольник при таких длинах. Это значит, необходимо сравнить суммы всех пар сторон с оставшейся третьей стороной. Чтобы треугольник существовал, сумма всегда должна быть больше отдельной стороны или, по крайней мере, не меньше, если учитывать так называемый вырожденный треугольник.

Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b , b + c , a + c . Первую сумму сравниваем с оставшейся стороной c , вторую — с a и третью — с b . Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.

Можно решить задачу сложнее. Если требуется также определить, какая из сторон больше суммы двух других, то решение может быть таким:

Особого смысла использовать переменную flag здесь нет. Она просто позволяет лишний раз не писать в программе строки, информирующие о том, что треугольник не существует. Большего внимания заслуживает использование вложенных конструкций if-else.

Видео:Существует ли город под Бермудским треугольником?Скачать

Треугольник — определение и основные свойства и виды треугольника

Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.

Видео:Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

Определение треугольника

Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.

Посмотрите на треугольник на рисунке.

У него три вершины — , , и три стороны , и . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут ([а-бэ-цэ]). А треугольник на вот этом рисунке

будут звать ([эм-эн-ка]).

По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.

В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.

Видео:IBLS — Существует ли треугольник, у которого все углы прямые? #shortsСкачать

Высота треугольника

В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.

Например, в треугольнике , высотой будет отрезок .

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.

В этом треугольнике три высоты , , .

Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.

Видео:100 Фактов о Бермудском Треугольнике, о Которых Вы не ЗналиСкачать

Виды треугольника

Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.

Виды треугольников по углам

В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный , треугольник бывает остроугольным, тупоугольным или прямоугольным.

Посмотрите на рисунки — перед вами три основных вида треугольника:

Виды треугольников по сторонам

Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.

На рисунке показаны равносторонний и равнобедренный треугольники.

Видео:А существует ли треугольник?Скачать

Свойства сторон треугольника

Треугольник имеет важные свойства и характеристики.

Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.

Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.

Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:

Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?

Решение: согласно свойству сторон треугольника, получим:

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.

Правило существования треугольника

Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.

Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.

Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.

Видео:Бермудский Треугольник - Загадка раскрыта!Скачать

Свойство углов в треугольнике

Сумма всех углов в треугольнике равна .

Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна .

Например, пусть известно, что в треугольнике , , , нужно найти .

Так как сумма углов в треугольнике равна , то находим:

.

Ответ: .

Видео:На Аляске есть Бермудский треугольник, и он еще более загадоченСкачать

Элементы композиции

Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.

А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:

Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.

💥 Видео

Бермудский треугольник | Почему? Вопросы мироздания | DiscoveryСкачать

Геометрия Существует ли треугольник ABC такой, что SinA = 0,4 AC = 18 см BC = 6 смСкачать

Что скрывает фрактальный треугольник? // Vital MathСкачать

Как появился знаменитый треугольник Карпмана? Психологическое значение библейских историй. Лекция №2Скачать

ВСЕ ТАЙНЫ БЕРМУДСКОГО ТРЕУГОЛЬНИКА [Топ Сикрет]Скачать

Треугольник со сторонами 1, 2 и 4 существует. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Краткая история Бермудского треугольникаСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Самое Жуткое Существо, Обнаруженное в Бермудском ТреугольникеСкачать

Ученые Наконец то Раскрыли Тайну Бермудского ТреугольникаСкачать

Решение простых задач на python | Существует ли треугольник с заданными сторонамиСкачать

Нечто космическое под Бермудским треугольником может раскрыть его тайныСкачать