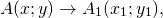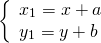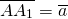Построить образ прямой при параллельном переносе на вектор (4 видео)

Построить образ прямой при параллельном переносе на вектор

Пусть — вектор пространства. Рассмотрим отображение пространства на себя, при котором образом любой точки M пространства является такая точка M ′ , что вектор ′ равен вектору : ′ = (рис. 23).

Можно доказать, что точка M имеет при данном отображении единственный образ — точку М ′ , а для точки М ′ существует единственный прообраз — точка М .

Таким образом, получаем биективное отображение пространства на себя, т. е. преобразование пространства, которое называют параллельным переносом на вектор .

Определение. Параллельным переносом на вектор называется такое преобразование пространства, при котором любая точка М отображается на такую точку M ′ , что выполняется векторное равенство: ′ = .

Иногда параллельный перенос называют коротко переносом. При этом вектор называют вектором переноса. Если при переносе на вектор точка М отображается на точку M ′ , то пишут: М ′ = ( М ) или ( M ) = M ′ .

Из определения следует, что параллельный перенос задаётся либо вектором, либо парой соответствующих точек ( М, М ′ ) .

Если при переносе на вектор точка М отображается на точку M ′ , то ′ = (рис. 24). Тогда = – . Значит, точка М ′ отображается на точку M переносом на вектор – , т. е. преобразование, обратное переносу на вектор , есть перенос на вектор – .

Перенос на нулевой вектор является тождественным преобразованием: ( М ) = М для любой точки М пространства.

5.2. Параллельный перенос в координатах

Пусть в прямоугольной системе координат Охyz задан вектор ( a ; b ; с ) . Найдём зависимость между координатами точки М ( x ; y ; z ) и её образа M ′ ( х ′ ; y ′ ; z ′ ) при переносе на вектор .

Так как M ′ = ( М ) , то ′ = (рис. 25). Вектор ′ имеет координаты: ′ ( x ′ – x ; y ′ – y ; z ′ – z ). Тогда векторное равенство ′ = равносильно системе трёх равенств x ′ – х = a, y ′ – у = b, z ′ – z = с, откуда

(1)

Соотношения (1) называются формулами параллельного переноса пространства на вектор ( a ; b ; c ) .

Докажем, что параллельный перенос пространства есть движение . Пусть: A ( x 1 ; y 1 ; z 1 ) и C ( x 2 ; y 2 ; z 2 ) — данные точки; A ′ ( ; ; ), C ′ ( ; ; ) — их образы при переносе на вектор ( a ; b ; с ). На основании (1) имеем

= x 1 + a, = y 1 + b, = z 1 + c,
= x 2 + a, = y 2 + b, = z 2 + c . (2)

Расстояние между точками А и C равно

Найдём расстояние между точками А ′ и C ′ .

Учитывая (2), получаем

| A ′ C ′ | = =
= = | AC| .

Таким образом, при параллельном переносе расстояние между точками сохраняется. Значит, параллельный перенос есть движение.

5.3. Свойства параллельного переноса

Можно доказать, что параллельный перенос отображает :

— прямую на параллельную ей прямую либо на себя;

— луч на сонаправленный с ним луч;

— вектор на равный ему вектор (на себя);

— плоскость на параллельную ей плоскость либо на себя.

Докажем, например, что параллельный перенос отображает плоскость на параллельную ей плоскость или на себя.

Действительно, параллельный перенос — движение, поэтому он отображает плоскость α на некоторую плоскость α′ . Докажем, что α′ || α или α′ совпадает с α .

На плоскости α выберем две пересекающиеся прямые a и b ; a ∩ b = O.

Пусть ( a ) = a ′ , ( b ) = b ′ (рис. 26). Тогда a || a ′ , b || b ′ .

Так как любое преобразование отображает пересечение фигур на пересечение их образов и прямые a и b пересекаются в точке O, то пересекаются и прямые a ′ и b ′ в такой точке O ′ , что O ′ = ( О ). Тогда либо плоскости α и α′ совпадают, либо по признаку параллельности плоскостей эти плоскости параллельны, что и требовалось доказать. ▼

Рассмотрим вопрос о неподвижных точках, неподвижных прямых и неподвижных плоскостях при параллельном переносе.

Неподвижных точек параллельный перенос на ненулевой вектор не имеет.

Неподвижной прямой при параллельном переносе на ненулевой вектор является любая прямая, параллельная вектору ; на каждой из этих прямых индуцируется параллельный перенос на вектор .

Неподвижной плоскостью при параллельном переносе на ненулевой вектор является любая плоскость, параллельная вектору ; на каждой из этих плоскостей индуцируется параллельный перенос на вектор .

Параллельный перенос, отображая любой вектор на себя, не меняет ориентацию пространства, следовательно, является движением первого рода.

Рассмотрим композицию двух переносов, заданных векторами и . Её обычно обозначают не ∘ , а + .

Пусть М — любая точка пространства. Перенос на вектор точку М отображает на такую точку М ′ , что ′ = (рис. 27). Последующий перенос на вектор точку М ′ отображает на такую точку M ″ , что ″ = . По правилу сложения векторов имеем ″ = ′ + ″ = + . Это означает, что ( + )( M ) = M ″ , т. e. перенoc на вектор ( + ) точку М отображает на точку М ″ .

Таким образом, композиция переносов на векторы и есть перенос на вектор + .

Так как + = + , то композиция переносов обладает свойством коммутативности: ( + )( M ) = ( + )( М ).

5 .4. Скользящая симметрия

Среди преобразований пространства важное место занимает «скользящая симметрия», представляющая собой композицию симметрии S α относительно плоскости α и параллельного переноса на вектор , который параллелен этой плоскости (рис. 28).

Отметим ряд характерных свойств скользящей симметрии:

— скользящая симметрия является движением (как композиция двух движений);

— скользящая симметрия не имеет неподвижных точек;

— любая прямая плоскости α , параллельная вектору переноса, является неподвижной прямой скользящей симметрии; на каждой из них индуцируется параллельный перенос;

— неподвижной плоскостью скользящей симметрии является не только плоскость симметрии α (на ней индуцируется параллельный перенос на вектор ) , а также любая плоскость, перпендикулярная плоскости α и параллельная вектору переноса (на каждой из таких плоскостей индуцируется скользящая симметрия, осью которой является прямая пересечения этой плоскости с плоскостью α , а вектором переноса — вектор );

— скользящая симметрия меняет ориентацию тетраэдра (значит, и ориентацию пространства), т. е. является движением второго рода;

— преобразованием, обратным скользящей симметрии, заданной плоскостью α и вектором , является скользящая симметрия, заданная той же плоскостью α и вектором – .

Попробуйте доказать самостоятельно, что композиция двух центральных симметрий есть параллельный перенос, причём Z B ∘ Z A = 2 . Наоборот, любой параллельный перенос может быть разложен (неоднозначно) в композицию двух центральных симметрий.

Содержание

Параллельный перенос
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
🌟 Видео

Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Параллельный перенос

Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.

Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.

1) Введём на плоскости декартовы координаты x, y.

Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.

Формулы параллельного переноса

Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)

то параллельный перенос задаётся формулами:

Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.

2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:

Свойства параллельного переноса

1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).

2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.

В алгебре параллельный перенос широко используется для построения графиков функций.

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Please wait.

Видео:11 класс, 12 урок, Параллельный переносСкачать

We are checking your browser. mathvox.ru

Видео:9 класс, 32 урок, Параллельный переносСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Урок 8. Параллельный перенос. Декартовы координаты на плоскости.Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6c64adc708401646 • Your IP : 178.45.231.185 • Performance & security by Cloudflare