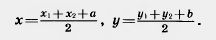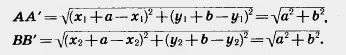Построить образ прямой при параллельном переносе

Видео:11 класс, 12 урок, Параллельный переносСкачать

We are checking your browser. mathvox.ru

Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6c5a233998b23aad • Your IP : 85.95.179.130 • Performance & security by Cloudflare

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Построить образ прямой при параллельном переносе

Параллельный перенос и его свойства

Видео:9 класс, 32 урок, Параллельный переносСкачать

Содержание

Видео:9 класс параллельный перенос. Построение игур при параллельном переносе.Скачать

Общие сведения о параллельном переносе

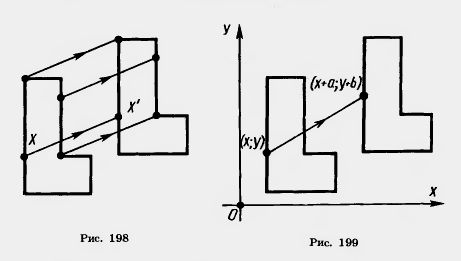
Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение.

Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x’ = x + а, у’ = у + b.

Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Свойства параллельного переноса

Параллельный перенос есть движение.

Действительно, две произвольные точки А(х₁; у₁) к В (х₂; у₂) переходят при параллельном переносе в точки А’ (х₁ +а; у₁ + b), В'(х₂ + а; y₂+b). Поэтому
АВ 2 =(х₂-х₁) 2 + (у₂-у₁ ) 2

Отсюда АВ=А’В’. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.

Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

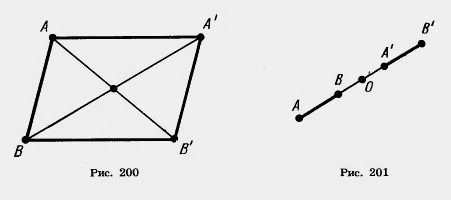
Действительно, пусть точки A (x₁; y₁) и В (x₂; y₂) переходят в точки A'(x₁+а; y₁ + b) и В’ (х₂ + а; y₂ + b) (рис. 200). Середина отрезка АВ’ имеет координаты

Те же координаты имеет и середина отрезка А’В. Отсюда следует, что диагонали четырехугольника АА’В’В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А’ и ВВ’ параллельны и равны.

Заметим, что у параллелограмма АА’В’В параллельны и две другие противолежащие стороны — АВ и А ‘В’. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).

Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА’. В случае, когда точка В лежит на прямой АА’, точка В’ тоже лежит на этой прямой, так как середина отрезка АВ’ совпадает с серединой отрезка ВА’ (рис. 201). Значит, все точки А, В, А’, В’ лежат на одной прямой. Далее,

Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние 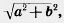а прямая АВ переходит в себя.

Видео:Урок 8. Параллельный перенос. Декартовы координаты на плоскости.Скачать

Повторение темы о параллельном переносе

Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом.

Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую.

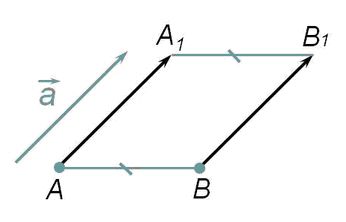
Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину.

Видео:ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ПОВОРОТ 9 класс геометрия АтанасянСкачать

Свойства, которыми обладает параллельный перенос в пространстве

• Во-первых, параллельный перенос является движением;
• Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;
• В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;
• В-четвертых, независимо от того, какими точками были A и A’, но точка A переходит в точку A’.
• В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Истрия и применение в науке

Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.

Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.

Видео:Параллельный перенос. Координаты точек при параллельном переносе. Геометрия 8 классСкачать

Примеры из жизни

В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.

А также, параллельный перенос можно встретить и в таких необычных ситуациях:

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Построить образ прямой при параллельном переносе

Пусть — вектор пространства. Рассмотрим отображение пространства на себя, при котором образом любой точки M пространства является такая точка M ′ , что вектор ′ равен вектору : ′ = (рис. 23).

Можно доказать, что точка M имеет при данном отображении единственный образ — точку М ′ , а для точки М ′ существует единственный прообраз — точка М .

Таким образом, получаем биективное отображение пространства на себя, т. е. преобразование пространства, которое называют параллельным переносом на вектор .

Определение. Параллельным переносом на вектор называется такое преобразование пространства, при котором любая точка М отображается на такую точку M ′ , что выполняется векторное равенство: ′ = .

Иногда параллельный перенос называют коротко переносом. При этом вектор называют вектором переноса. Если при переносе на вектор точка М отображается на точку M ′ , то пишут: М ′ = ( М ) или ( M ) = M ′ .

Из определения следует, что параллельный перенос задаётся либо вектором, либо парой соответствующих точек ( М, М ′ ) .

Если при переносе на вектор точка М отображается на точку M ′ , то ′ = (рис. 24). Тогда = – . Значит, точка М ′ отображается на точку M переносом на вектор – , т. е. преобразование, обратное переносу на вектор , есть перенос на вектор – .

Перенос на нулевой вектор является тождественным преобразованием: ( М ) = М для любой точки М пространства.

5.2. Параллельный перенос в координатах

Пусть в прямоугольной системе координат Охyz задан вектор ( a ; b ; с ) . Найдём зависимость между координатами точки М ( x ; y ; z ) и её образа M ′ ( х ′ ; y ′ ; z ′ ) при переносе на вектор .

Так как M ′ = ( М ) , то ′ = (рис. 25). Вектор ′ имеет координаты: ′ ( x ′ – x ; y ′ – y ; z ′ – z ). Тогда векторное равенство ′ = равносильно системе трёх равенств x ′ – х = a, y ′ – у = b, z ′ – z = с, откуда

(1)

Соотношения (1) называются формулами параллельного переноса пространства на вектор ( a ; b ; c ) .

Докажем, что параллельный перенос пространства есть движение . Пусть: A ( x 1 ; y 1 ; z 1 ) и C ( x 2 ; y 2 ; z 2 ) — данные точки; A ′ ( ; ; ), C ′ ( ; ; ) — их образы при переносе на вектор ( a ; b ; с ). На основании (1) имеем

= x 1 + a, = y 1 + b, = z 1 + c,
= x 2 + a, = y 2 + b, = z 2 + c . (2)

Расстояние между точками А и C равно

.

Найдём расстояние между точками А ′ и C ′ .

Учитывая (2), получаем

| A ′ C ′ | = =
= = | AC| .

Таким образом, при параллельном переносе расстояние между точками сохраняется. Значит, параллельный перенос есть движение.

5.3. Свойства параллельного переноса

Можно доказать, что параллельный перенос отображает :

— прямую на параллельную ей прямую либо на себя;

— луч на сонаправленный с ним луч;

— вектор на равный ему вектор (на себя);

— плоскость на параллельную ей плоскость либо на себя.

Докажем, например, что параллельный перенос отображает плоскость на параллельную ей плоскость или на себя.

Действительно, параллельный перенос — движение, поэтому он отображает плоскость α на некоторую плоскость α′ . Докажем, что α′ || α или α′ совпадает с α .

На плоскости α выберем две пересекающиеся прямые a и b ; a ∩ b = O.

Пусть ( a ) = a ′ , ( b ) = b ′ (рис. 26). Тогда a || a ′ , b || b ′ .

Так как любое преобразование отображает пересечение фигур на пересечение их образов и прямые a и b пересекаются в точке O, то пересекаются и прямые a ′ и b ′ в такой точке O ′ , что O ′ = ( О ). Тогда либо плоскости α и α′ совпадают, либо по признаку параллельности плоскостей эти плоскости параллельны, что и требовалось доказать. ▼

Рассмотрим вопрос о неподвижных точках, неподвижных прямых и неподвижных плоскостях при параллельном переносе.

Неподвижных точек параллельный перенос на ненулевой вектор не имеет.

Неподвижной прямой при параллельном переносе на ненулевой вектор является любая прямая, параллельная вектору ; на каждой из этих прямых индуцируется параллельный перенос на вектор .

Неподвижной плоскостью при параллельном переносе на ненулевой вектор является любая плоскость, параллельная вектору ; на каждой из этих плоскостей индуцируется параллельный перенос на вектор .

Параллельный перенос, отображая любой вектор на себя, не меняет ориентацию пространства, следовательно, является движением первого рода.

Рассмотрим композицию двух переносов, заданных векторами и . Её обычно обозначают не ∘ , а + .

Пусть М — любая точка пространства. Перенос на вектор точку М отображает на такую точку М ′ , что ′ = (рис. 27). Последующий перенос на вектор точку М ′ отображает на такую точку M ″ , что ″ = . По правилу сложения векторов имеем ″ = ′ + ″ = + . Это означает, что ( + )( M ) = M ″ , т. e. перенoc на вектор ( + ) точку М отображает на точку М ″ .

Таким образом, композиция переносов на векторы и есть перенос на вектор + .

Так как + = + , то композиция переносов обладает свойством коммутативности: ( + )( M ) = ( + )( М ).

5 .4. Скользящая симметрия

Среди преобразований пространства важное место занимает «скользящая симметрия», представляющая собой композицию симметрии S α относительно плоскости α и параллельного переноса на вектор , который параллелен этой плоскости (рис. 28).

Отметим ряд характерных свойств скользящей симметрии:

— скользящая симметрия является движением (как композиция двух движений);

— скользящая симметрия не имеет неподвижных точек;

— любая прямая плоскости α , параллельная вектору переноса, является неподвижной прямой скользящей симметрии; на каждой из них индуцируется параллельный перенос;

— неподвижной плоскостью скользящей симметрии является не только плоскость симметрии α (на ней индуцируется параллельный перенос на вектор ) , а также любая плоскость, перпендикулярная плоскости α и параллельная вектору переноса (на каждой из таких плоскостей индуцируется скользящая симметрия, осью которой является прямая пересечения этой плоскости с плоскостью α , а вектором переноса — вектор );

— скользящая симметрия меняет ориентацию тетраэдра (значит, и ориентацию пространства), т. е. является движением второго рода;

— преобразованием, обратным скользящей симметрии, заданной плоскостью α и вектором , является скользящая симметрия, заданная той же плоскостью α и вектором – .

Попробуйте доказать самостоятельно, что композиция двух центральных симметрий есть параллельный перенос, причём Z B ∘ Z A = 2 . Наоборот, любой параллельный перенос может быть разложен (неоднозначно) в композицию двух центральных симметрий.

📸 Видео

Параллельные прямые циркулемСкачать

Тема: Движения. Урок: Движения на плоскости. Параллельный переносСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

9 класс. Параллельный переносСкачать

СТЕРЕОМЕТРИЯ. Построение сечений многогранников методом параллельного переносаСкачать

8 класс, 9 урок, Осевая и центральная симметрияСкачать

Свойства параллельного переноса. Геометрия 8 классСкачать

Как строить сечения параллелепипедаСкачать