Как построить 10 угольник в окружности с помощью циркуля

Десятиугольник, как и все многоугольники, можно легко построить с помощью циркуля и линейки. Существует два несложных способа для решения данной интересной и необычной задачи.
Вам понадобится

Многоугольником называется замкнутая ломаная. Десятиугольник, соответственно, — это замкнутая ломаная, состоящая из 10 углов и 10 отрезков. Построить произвольный десятиугольник несложно. Для этого надо взять 10 любых точек, не лежащих на одной прямой, и соединить эти точки отрезками так, чтобы получилась замкнутая фигура. Причем должно выполняться условие: две любые точки внутри получившейся фигуры должны соединяться линией, не пересекающей границы фигуры. Если данное условие не выполняется, то построенная фигура не является многоугольником.

1 способ: С помощью циркуля начертите окружность. Используя транспортир, разделите ее на 10 равных секторов по 36 градусов каждый (360:10 = 36). Затем соедините последовательно все точки, отмеченные на окружности.

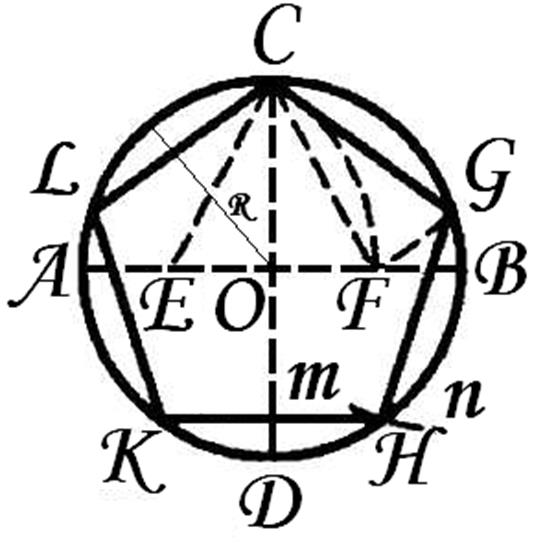
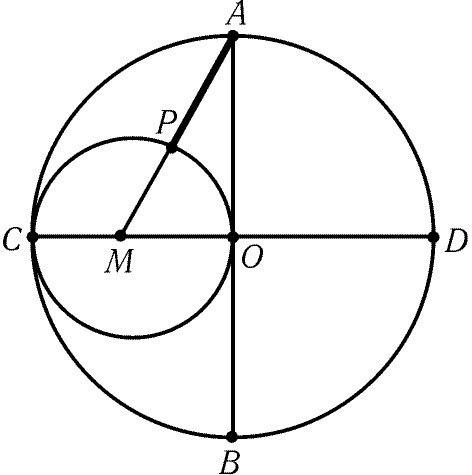
2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.

Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.

Видео:Построение девятиугольника циркулем, приближенноеСкачать

10 Угольник вписанный в окружность

Десятиугольник, вписанный в окружность

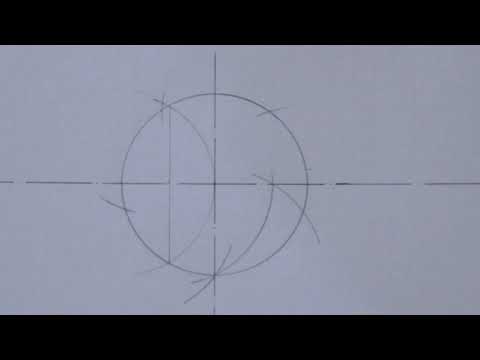
Проводим два взаимно перпендикулярных диаметра АВ и CD. Делим пополам радиус АО в точке Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. OF есть сторона искомой фигуры. С помощью циркуля, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры. Подобно построению пятиугольника, вписанного в окружность.

Десятиугольник, описанный около окружности

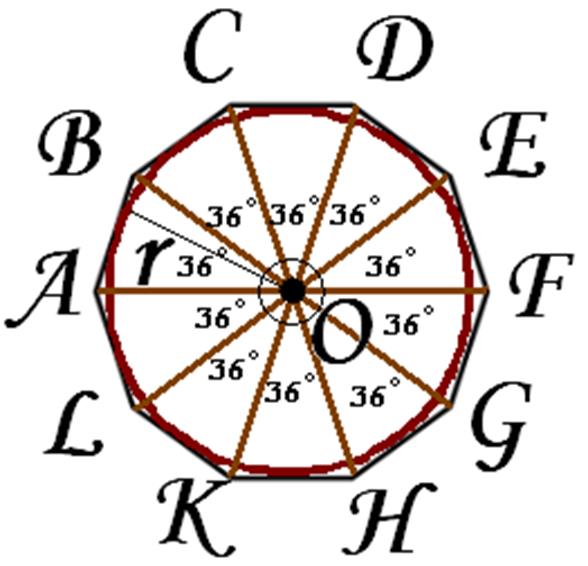
Имеем исходную окружность с центром в точке O. Так как сумма углов, составляющих центральный угол окружности, равна 360°. Делим данный угол на 10 частей (т.к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8924 – | 7231 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

• Как начертить десятиугольник
• Как начертить угол без транспортира
• Как построить правильный восьмиугольник

• – циркуль;
• – линейка.

2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.

Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.

Правильный десятиугольник
Сторон и вершин	10
Символ Шлефли
Внутренний угол	144°
Симметрия	Диэдрическая ( D 10 > ), порядок 20.

Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.

Видео:Построение 10 угольника циркулемСкачать

Содержание

Видео:Геометрия - Построение десятиугольникаСкачать

Правильный десятиугольник [ править | править код ]

У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.

Площадь правильного десятиугольника равна (t — длина стороны):

A = 5 2 t 2 c t g π 10 = 5 t 2 2 5 + 2 5 ≈ 7.694 t 2 . >t^ ctg >= > > >>>approx 7.694t^ .>

Альтернативная формула A = 2.5 d t , где d – расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:

d = 2 t ( cos ⁡ 3 π 10 + cos ⁡ π 10 ) , >+cos >
ight),>

и может быть представлен в радикалах как

d = t 5 + 2 5 . >>>.>

Сторона правильного десятиугольника, вписанного в единичную окружность, равна 5 − 1 2 = 1 φ >-1> >= >> , где φ – золотое сечение.

Радиус описанной окружности десятиугольника равен

R = 5 + 1 2 t , >+1> >t,>

а радиус вписанной окружности

r = 5 + 2 5 2 t . >>> >t.>

Построение [ править | править код ]

По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку.

Иначе его можно построить следующим образом:

1. Построить сначала правильный пятиугольник.
2. Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
3. Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.

Видео:Построение пятиугольника циркулем и линейкойСкачать

Разбиение правильного десятиугольника [ править | править код ]

Гарольдом Коксетером было доказано, что правильный 2 m -угольник можно разбить на m ( m − 1 ) 2 >> ромбов. Для декагона m = 5 , так что он может быть разбит на 10 ромбов.

Видео:Построение 8 угольника циркулемСкачать

Пространственный десятиугольник [ править | править код ]

Правильные пространственные десятиугольники
#	#	#

Пентаграммная антипризма с перекрёстом

Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.

У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D_5d [2 + ,10] симметрией порядка 20.

Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники.

Ортогональные проекции многогранников
Додекаэдр	Икосаэдр	Икосододекаэдр	Ромботриаконтаэдр

Многоугольники Петри [ править | править код ]

Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера.

Видео:Построение 12 угольника циркулемСкачать

Как построить 10 угольник в окружности

Видео:Как разделить окружность на 10 частей How to divide a circle into 10 partsСкачать

Построение правильных многоугольников

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Тема этого видеоурока – «Построение правильных многоугольников». На данном занятии мы рассмотрим способы построения правильных многоугольников с помощью циркуля и линейки. Также еще раз дадим определение правильному многоугольнику, изобразим его графически, после чего еще раз убедимся, что центры вписанной и описанной окружностей вокруг такой фигуры будут совпадать.

Видео:Построение пятиугольника циркулемСкачать

Как построить десятиугольник в окружности

Видео:Как построить одиннадцатиугольник и 11 конечную звезду циркулемСкачать

Построение правильных многоугольников. Решение задач

Разделы: Математика

Цели урока: закрепить знание формул стороны и площади правильного многоугольника, совершенствовать навык построения правильных многоугольников, научить строить правильный десятиугольник и правильный пятиугольник.

1. Проверка домашнего задания: пункт 108, №№ 1081, 1093, 1094(а,б).

Учебник Геометрия 7 — 9, Л.С. Атанасян.2003г.

а) = 180 = 60

б) = 180 = 3 · 36

в) = 180 = 120

г) = 180 = 144

д) = · 180 = 160

Дано: АВС — правильный

Окр.(О;R) — описана около АВС

Окр.(О;r) — вписанна в АВС

1. АО — биссектриса А OАD = 30

2. AOD — прямоугольный, т.к. OD = r проведён в точку касания (теорема о касательной к окружности).

3. В прямоугольном AOD катет r лежащий против угла в 30 равен половине гипотенузы R, т.е. R = 2r — ч.т.д.

Задача № 1094(а,б) (данное задание на закрепление знания формул:

S = Рr, a_n = 2R, r = R )

a₄ = 2R = 2 * 3 * = 2 * 3* = 6 см,

r = 3 * = 3 * = 3 см,

S = Рr = · 24 · 3 = 36 см 2

б) Решение: a₃ = = 8 см

Выразим r через a_n : r = ( a_n * ctg)/2

r = 4* ctg = см

S = (1/2)Рr = 16 см 2 Ответ: 16 см 2 .

2. Актуализация знаний учащихся (устный опрос):

1. Какой многоугольник называется правильным?

2. Какая окружность называется вписанной в многоугольник?

3. По какой формуле можно найти сторону правильного n-угольника? (записать на доске)

4. Какая точка называется центром правильного многоугольника?

5. Можно ли найти площадь правильного шестиугольника, зная только радиус вписанной в него окружности? Как это сделать? (показать на доске)

3. Изучение нового материала.

Строить правильные треугольники и четырёхугольники с помощью циркуля и линейки мы уже умеем. Рассмотрим способ построения правильного шестиугольника.

Задача № 1 из п.109 (работа с учебником).

Построить правильный шестиугольник, сторона которого равна данному отрезку.

1. Строим окружность радиусом R равным данному отрезку.

2. На окружности произвольно выбираем точку A₁ .

3. Не меняя раствора циркуля, на окружности откладываем точку A₂ , так чтобы A₁A₂ = R.

4. Аналогично от точки A₂ откладываем точку A₃ и т. д. до точки A₆ .

5. Соединяя последовательно построенные точки отрезками, получаем искомый правильный шестиугольник .

Доказательство: (можно провести устно)

1. Стороны 6 — угольника равны (по построению). (*)

2. О A₁A₂ = О A₂A₃ = О A₃A₄ = : = О A₆A₁ — по третьему признаку равенства -ов.

Все они равносторонние. A₁A₂A₃ = : = A₆A₁A₂ = 120° (**)

3. Из (*) и (**) A₁A₂A₃A₄A₅A₆ — правильный 6 — угольник — ч.т.д.

11Задача № 1279. На рисунке 370 изображён правильный десятиугольник, вписанный в окружность радиуса R, АС — биссектриса угла ОАВ. Докажите, что:

а) AВС

ОАВ

б) АВ = АС = ОС = R

(т.к. данная задача является задачей повышенной трудности, то перед решением её у доски необходимо дать учащимся две — три минуты на обдумывание, если не будет идей, то задавать наводящие вопросы.)

1. Рассмотрим равнобедренный ОАВ:

АО и ВО — биссектрисы углов правильного десятиугольника ( = 144)

Следовательно: = = 72, а значит = 36.

2. = 72, а т.к. АС — биссектриса этого угла, то = 36, т.е. = (*)

3. — общий для AВС и ОАВ. (**)

4. Из (*) и (**) следует (по первому признаку подобия треугольников),

что AВС

ОАВ — ч.т.д.

б) 1. В AВС: = 36, = 72 = 72, значит АВ = АС.

2. В ОАС: = = 36 АС = ОС

3. Обозначим АВ через х, ОС также равно х. АО = R , BC = R — x .

Из подобия AВС и ОАВ следует: x 2 + Rх — R 2 = 0

(получили квадратное уравнение относительно х)

x₁ = — решений нет, т.к. длина отрезка не может быть отрицательной

x₂ = = R — ч.т.д.

Исследование: зададимся вопросом — чему равен и .

1. В ОАВ проведём медиану ОК (она же высота и биссектриса).

АК = x/2= R·

R = R·

Итак: =

2. = 2* = 2* * = · = = =

=

11Задача № 1280. Докажите, что отрезок АК, изображённый на рисунке, равен стороне правильного десятиугольника, вписанного в окружность с центром О.

А и В Окр(О;R);

АООВ;

Окр(С; r = СВ)АС = К

Доказать: АК = R (по предыдущей задачи)

1. АО = R, OC = , AC = = ;

2. КС = , АК = АС — КС = — = R — ч.т.д.

Вывод: данный способ можно использовать для построения правильного десятиугольника.+

4. Закрепление изученного материала.

Задача № 1283: В данную окружность впишите правильный пятиугольник.

Мы рассмотрим иной способ построения, не тот который предлагают в ответе.

1. Строим окружность произвольного радиуса R и проводим два взаимно перпендикулярных диаметра АВ и СD.

2. Делим пополам радиус АО точкой Е.

3. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F.

4. Из С радиусом CF проводим дугу FG, пересекая ею данную окружность в точке G; CG(равная CF) есть одна сторона искомой фигуры.

5. Проводим тем же радиусом дугу из точки G как из центра, получаем ещё одну вершину Н искомой фигуры и т. д.

6. CGHKL — правильный пятиугольник.

1. Сторона правильного пятиугольника вписанного в Окр.(О;R) равна .

11 ОМ — биссектриса, медиана и высота равнобедренного ОСG.

СМ = R a₅ = 2СМ = 2 R

Учитывая, что = ,

окончательно получаем: a₅ = .

2. У нас по построению

1) ЕО = ; ЕС = ЕF =

2) OF = EF — EO = R

3) CG = CF = = = .

Итак, по построению CG = — ч.т.д.

5. Подведение итогов урока.

Домашнее задание: пункт 109, № 1282, №1284.

Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

10 Угольник вписанный в окружность

Десятиугольник, вписанный в окружность

Проводим два взаимно перпендикулярных диаметра АВ и CD. Делим пополам радиус АО в точке Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. OF есть сторона искомой фигуры. С помощью циркуля, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры. Подобно построению пятиугольника, вписанного в окружность.

Десятиугольник, описанный около окружности

Имеем исходную окружность с центром в точке O. Так как сумма углов, составляющих центральный угол окружности, равна 360°. Делим данный угол на 10 частей (т.к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8924 – | 7231 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

• Как начертить десятиугольник
• Как начертить угол без транспортира
• Как построить правильный восьмиугольник

• – циркуль;
• – линейка.

2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.

Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.

Правильный десятиугольник
Сторон и вершин	10
Символ Шлефли
Внутренний угол	144°
Симметрия	Диэдрическая ( D 10 > ), порядок 20.

Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.

Видео:Деление окружности на равные части с помощью циркуляСкачать

Содержание

Видео:Построение 7 угольника циркулем, приближенноеСкачать

Правильный десятиугольник [ править | править код ]

У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.

Площадь правильного десятиугольника равна (t — длина стороны):

A = 5 2 t 2 c t g π 10 = 5 t 2 2 5 + 2 5 ≈ 7.694 t 2 . >t^ ctg >= > > >>>approx 7.694t^ .>

Альтернативная формула A = 2.5 d t , где d – расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:

d = 2 t ( cos ⁡ 3 π 10 + cos ⁡ π 10 ) , >+cos >
ight),>

и может быть представлен в радикалах как

d = t 5 + 2 5 . >>>.>

Сторона правильного десятиугольника, вписанного в единичную окружность, равна 5 − 1 2 = 1 φ >-1> >= >> , где φ – золотое сечение.

Радиус описанной окружности десятиугольника равен

R = 5 + 1 2 t , >+1> >t,>

а радиус вписанной окружности

r = 5 + 2 5 2 t . >>> >t.>

Построение [ править | править код ]

По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку.

Иначе его можно построить следующим образом:

1. Построить сначала правильный пятиугольник.
2. Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
3. Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.

Видео:4K Как построить десятиугольник, regular decagon constructionСкачать

Разбиение правильного десятиугольника [ править | править код ]

Гарольдом Коксетером было доказано, что правильный 2 m -угольник можно разбить на m ( m − 1 ) 2 >> ромбов. Для декагона m = 5 , так что он может быть разбит на 10 ромбов.

Видео:Красивое деление окружности на 20 частей циркулемСкачать

Пространственный десятиугольник [ править | править код ]

Правильные пространственные десятиугольники
#	#	#

Пентаграммная антипризма с перекрёстом

Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.

У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D_5d [2 + ,10] симметрией порядка 20.

Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники.

Ортогональные проекции многогранников
Додекаэдр	Икосаэдр	Икосододекаэдр	Ромботриаконтаэдр

Многоугольники Петри [ править | править код ]

Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера.

Видео:Построение шестнадцатиугольника циркулемСкачать

Десятиугольник: правильный, неправильный, свойства, примеры

Видео:Деление окружности на 5 равных частейСкачать

Содержание:

В десятиугольник представляет собой плоскую фигуру в форме многоугольника с 10 сторонами и 10 вершинами или точками. Декагоны могут быть правильными или неправильными, в первом случае все стороны и внутренние углы имеют одинаковую величину, а во втором стороны и / или углы отличаются друг от друга.

На рисунке 1 показаны примеры десятиугольника каждого типа, и, как мы видим, правильный десятиугольник очень симметричен.

Основными элементами каждого десятиугольника являются:

-Стороны, отрезки линии, которые при соединении образуют десятиугольник.

-Vertices или точки между каждой последовательной стороной.

-Внутренние и внешние углы между соседними сторонами.

-Диагональные, сегменты, соединяющие две непоследовательные вершины.

Вершины названы заглавными буквами, как показано на рисунке 1, где использовались первые буквы алфавита, но можно использовать любую букву.

Стороны обозначены двумя буквами вершин, между которыми они находятся, например, сторона AB — это сторона между вершинами A и B. То же самое сделано с диагоналями, поэтому у нас есть диагональ AF, которая соединяет точки A и F.

Для углов мы используем этот символ: ∠, похожий на наклонную L. Например, угол ∠ ABC — это угол, вершиной которого является B, а сторонами являются отрезки AB и BC.

Видео:1 2 2 деление окружности на 5 равных частейСкачать

Обычный десятиугольник

В правильном десятиугольнике все стороны имеют одинаковую меру, как и внутренние углы. Поэтому говорят, что это равносторонний (равные стороны) и равносторонний (равные углы). Это очень симметричная фигура

Видео:деление окружности на произвольное число частейСкачать

Внутренние углы правильного десятиугольника

Чтобы найти меру внутренних углов правильного многоугольника, включая правильный десятиугольник, используется следующая формула:

-I — мера угла в градусах.

-n — количество сторон многоугольника. В случае десятиугольника n = 10.

Подставляя n = 10 в предыдущую формулу, получаем следующее:

Говорят, что многоугольник выпуклый если его угловые размеры меньше 180 °, иначе многоугольник вогнутый. Поскольку любой внутренний угол правильного десятиугольника составляет 144º и меньше 180º, то это выпуклый многоугольник.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сумма внутренних углов

Сумма внутренних углов любого многоугольника в градусах:

S = (n-2) x 180 °; n всегда больше 2

В этой формуле мы имеем:

-S — это сумма размеров внутренних углов.

-n — количество сторон. Для десятиугольника n = 10

Применяя формулу для n = 10, получаем:

S = (10 — 2) x 180º = 1440º

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Внешние углы

Между одной стороной и продолжением соседней стороны образуется внешний угол, посмотрим:

Сумма угла ∠ ABC плюс внешний угол составляет 180 °, то есть они равны дополнительный. Следовательно, внешний угол равен 180º-144º = 36º, как мы видим на рисунке.

Количество диагоналей

Как было сказано ранее, диагонали — это отрезки, соединяющие непоследовательные вершины. Сколько диагоналей мы можем нарисовать в десятиугольнике? Когда количество вершин невелико, их легко сосчитать, но когда это число увеличивается, вы можете потерять счет.

К счастью, есть формула, по которой можно узнать, сколько диагоналей многоугольника. п стороны:

Подставляем десятиугольник n = 10 и получаем:

D = 10 х (10 — 3) / 2 = 35

В правильном десятиугольнике все диагонали пересекаются в одной точке, которая является центром фигуры:

Центр

Центр многоугольника определяется как точка, равноудаленная от любой вершины. На рисунке выше центр совпадает с точкой пересечения всех диагоналей.

Периметр

Если у правильного десятиугольника есть сторона a, его периметр P равен сумме всех сторон:

Площадь

Зная длину к сбоку площадь правильного десятиугольника рассчитывается по формуле:

Приблизительная формула для площади:

И третий способ найти площадь — по длине апофемы L_К. Это сегмент, который соединяет середину одной стороны с центром многоугольника.

В этом случае площадь можно рассчитать по формуле:

Неправильный десятиугольник

Неправильный десятиугольник не является равносторонним или равноугольным, и обычно ему не хватает симметрии правильной фигуры, хотя некоторые десятиугольники могут иметь ось симметрии.

Они также могут быть выпуклыми или вогнутыми, если внутренние углы превышают 180º.

Неправильный десятиугольник на фиг. 1 вогнут, поскольку некоторые из его внутренних углов больше 180 °. Ясно, что существует множество комбинаций углов и сторон, которые приводят к неправильному десятиугольнику.

В любом случае верно, что:

-Внутренние углы неправильного десятиугольника также составляют в сумме 1440º.

-Также имеет 35 диагоналей.

Площадь неправильного десятиугольника по гауссовским определителям

В общем, не существует единой формулы для определения площади неправильного многоугольника, поскольку стороны и углы разные. Однако его можно найти, зная координаты вершин и вычисливГауссовские детерминанты:

-Позвоним (х_п , Y_п ) к координатам вершин, причем п варьируется от 1 до 10.

-Вы можете начать с любой вершины, до которой координаты (x₁, Y₁ ). Теперь нам нужно подставить значения каждой координаты в эту формулу:

Где детерминанты — это именно операции в скобках.

-Важно отметить, что последний определитель снова включает первую вершину вместе с последней. Для десятиугольника это будет выглядеть так:

Важный: Полоски имеют абсолютное значение и означают, что окончательный результат дается с положительным знаком. всегда.

Процедура может быть трудоемкой, если у фигуры много вершин, в случае с десятиугольником — 10 операций, поэтому желательно составить таблицу или список.

Упражнение решено

Вычислите площадь неправильного десятиугольника, показанного на рисунке. Координаты вершин — A, B, C… J, значения которых показаны слева.

Решение

-Делаем каждую из 10 операций:

• 2×6 – 4×0 = 12 – 0 =12
• 0×4 – 6×(-2) = 0 + 12 =12
• (-2)×7- 4×(-5) = -14 + 20 = 6
• (-5)×2 – 7×(-6) = -10 + 42 = 32
• (-6)×(-4) – 2×(-4) = 24 + 8 =32
• (-4)×(-2) – (-4)×(-2) = 8 – 8 =0
• (-2)×0 – (-2)×(-1) =0 -2
• (-1)×0 – 0×(2) = 0 – 0 = 0
• 2×2 – 0×8 = 4 – 0 = 4
• 8×4 -2×2 = 32 – 4 = 28

-Давайте добавим результаты:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Положительный результат получается даже без столбцов абсолютного значения, но если он отрицательный, знак меняется.

-Предыдущий результат делится на 2, и это площадь многоугольника:

Свойства Десятиугольника

Вот краткое изложение общих свойств десятиугольника, правильного или неправильного:

-У него 10 сторон и 10 вершин.

-Сумма внутренних углов 1440º.

-Есть 35 диагоналей.

-Периметр — это сумма всех сторон.

-Вы можете создавать треугольники внутри многоугольника, рисуя сегменты от одной вершины ко всем остальным. В десятиугольнике можно нарисовать 8 треугольников таким образом, как показано ниже:

Ссылки

1. Александр, Д. 2013. Геометрия. 5-е. Издание. Cengage Learning.
2. Decagon.com. Декагон. Получено с: decagono.com
3. Открытый справочник по математике. Декагон. Получено с: mathopenref.com.
4. Sangaku Maths. Элементы многоугольника и их классификация. Получено с: sangakoo.com.
5. Википедия. Декагон. Получено с: es.wikipedia.com.

80 лучших слов о любви, которые затронут ваше сердце

Плодоводство: история, характеристики, виды, социально-экономическое значение

Десятиугольник: правильный, неправильный, свойства, примеры

Содержание:

В десятиугольник представляет собой плоскую фигуру в форме многоугольника с 10 сторонами и 10 вершинами или точками. Декагоны могут быть правильными или неправильными, в первом случае все стороны и внутренние углы имеют одинаковую величину, а во втором стороны и / или углы отличаются друг от друга.

На рисунке 1 показаны примеры десятиугольника каждого типа, и, как мы видим, правильный десятиугольник очень симметричен.

Основными элементами каждого десятиугольника являются:

-Стороны, отрезки линии, которые при соединении образуют десятиугольник.

-Vertices или точки между каждой последовательной стороной.

-Внутренние и внешние углы между соседними сторонами.

-Диагональные, сегменты, соединяющие две непоследовательные вершины.

Вершины названы заглавными буквами, как показано на рисунке 1, где использовались первые буквы алфавита, но можно использовать любую букву.

Стороны обозначены двумя буквами вершин, между которыми они находятся, например, сторона AB — это сторона между вершинами A и B. То же самое сделано с диагоналями, поэтому у нас есть диагональ AF, которая соединяет точки A и F.

Для углов мы используем этот символ: ∠, похожий на наклонную L. Например, угол ∠ ABC — это угол, вершиной которого является B, а сторонами являются отрезки AB и BC.

Обычный десятиугольник

В правильном десятиугольнике все стороны имеют одинаковую меру, как и внутренние углы. Поэтому говорят, что это равносторонний (равные стороны) и равносторонний (равные углы). Это очень симметричная фигура

Внутренние углы правильного десятиугольника

Чтобы найти меру внутренних углов правильного многоугольника, включая правильный десятиугольник, используется следующая формула:

-I — мера угла в градусах.

-n — количество сторон многоугольника. В случае десятиугольника n = 10.

Подставляя n = 10 в предыдущую формулу, получаем следующее:

Говорят, что многоугольник выпуклый если его угловые размеры меньше 180 °, иначе многоугольник вогнутый. Поскольку любой внутренний угол правильного десятиугольника составляет 144º и меньше 180º, то это выпуклый многоугольник.

Сумма внутренних углов

Сумма внутренних углов любого многоугольника в градусах:

S = (n-2) x 180 °; n всегда больше 2

В этой формуле мы имеем:

-S — это сумма размеров внутренних углов.

-n — количество сторон. Для десятиугольника n = 10

Применяя формулу для n = 10, получаем:

S = (10 — 2) x 180º = 1440º

Внешние углы

Между одной стороной и продолжением соседней стороны образуется внешний угол, посмотрим:

Сумма угла ∠ ABC плюс внешний угол составляет 180 °, то есть они равны дополнительный. Следовательно, внешний угол равен 180º-144º = 36º, как мы видим на рисунке.

Количество диагоналей

Как было сказано ранее, диагонали — это отрезки, соединяющие непоследовательные вершины. Сколько диагоналей мы можем нарисовать в десятиугольнике? Когда количество вершин невелико, их легко сосчитать, но когда это число увеличивается, вы можете потерять счет.

К счастью, есть формула, по которой можно узнать, сколько диагоналей многоугольника. п стороны:

Подставляем десятиугольник n = 10 и получаем:

D = 10 х (10 — 3) / 2 = 35

В правильном десятиугольнике все диагонали пересекаются в одной точке, которая является центром фигуры:

Центр

Центр многоугольника определяется как точка, равноудаленная от любой вершины. На рисунке выше центр совпадает с точкой пересечения всех диагоналей.

Периметр

Если у правильного десятиугольника есть сторона a, его периметр P равен сумме всех сторон:

Площадь

Зная длину к сбоку площадь правильного десятиугольника рассчитывается по формуле:

Приблизительная формула для площади:

И третий способ найти площадь — по длине апофемы L_К. Это сегмент, который соединяет середину одной стороны с центром многоугольника.

В этом случае площадь можно рассчитать по формуле:

Неправильный десятиугольник

Неправильный десятиугольник не является равносторонним или равноугольным, и обычно ему не хватает симметрии правильной фигуры, хотя некоторые десятиугольники могут иметь ось симметрии.

Они также могут быть выпуклыми или вогнутыми, если внутренние углы превышают 180º.

Неправильный десятиугольник на фиг. 1 вогнут, поскольку некоторые из его внутренних углов больше 180 °. Ясно, что существует множество комбинаций углов и сторон, которые приводят к неправильному десятиугольнику.

В любом случае верно, что:

-Внутренние углы неправильного десятиугольника также составляют в сумме 1440º.

-Также имеет 35 диагоналей.

Площадь неправильного десятиугольника по гауссовским определителям

В общем, не существует единой формулы для определения площади неправильного многоугольника, поскольку стороны и углы разные. Однако его можно найти, зная координаты вершин и вычисливГауссовские детерминанты:

-Позвоним (х_п , Y_п ) к координатам вершин, причем п варьируется от 1 до 10.

-Вы можете начать с любой вершины, до которой координаты (x₁, Y₁ ). Теперь нам нужно подставить значения каждой координаты в эту формулу:

Где детерминанты — это именно операции в скобках.

-Важно отметить, что последний определитель снова включает первую вершину вместе с последней. Для десятиугольника это будет выглядеть так:

Важный: Полоски имеют абсолютное значение и означают, что окончательный результат дается с положительным знаком. всегда.

Процедура может быть трудоемкой, если у фигуры много вершин, в случае с десятиугольником — 10 операций, поэтому желательно составить таблицу или список.

Упражнение решено

Вычислите площадь неправильного десятиугольника, показанного на рисунке. Координаты вершин — A, B, C… J, значения которых показаны слева.

Решение

-Делаем каждую из 10 операций:

• 2×6 – 4×0 = 12 – 0 =12
• 0×4 – 6×(-2) = 0 + 12 =12
• (-2)×7- 4×(-5) = -14 + 20 = 6
• (-5)×2 – 7×(-6) = -10 + 42 = 32
• (-6)×(-4) – 2×(-4) = 24 + 8 =32
• (-4)×(-2) – (-4)×(-2) = 8 – 8 =0
• (-2)×0 – (-2)×(-1) =0 -2
• (-1)×0 – 0×(2) = 0 – 0 = 0
• 2×2 – 0×8 = 4 – 0 = 4
• 8×4 -2×2 = 32 – 4 = 28

-Давайте добавим результаты:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Положительный результат получается даже без столбцов абсолютного значения, но если он отрицательный, знак меняется.

-Предыдущий результат делится на 2, и это площадь многоугольника:

Свойства Десятиугольника

Вот краткое изложение общих свойств десятиугольника, правильного или неправильного:

-У него 10 сторон и 10 вершин.

-Сумма внутренних углов 1440º.

-Есть 35 диагоналей.

-Периметр — это сумма всех сторон.

-Вы можете создавать треугольники внутри многоугольника, рисуя сегменты от одной вершины ко всем остальным. В десятиугольнике можно нарисовать 8 треугольников таким образом, как показано ниже:

Ссылки

1. Александр, Д. 2013. Геометрия. 5-е. Издание. Cengage Learning.
2. Decagon.com. Декагон. Получено с: decagono.com
3. Открытый справочник по математике. Декагон. Получено с: mathopenref.com.
4. Sangaku Maths. Элементы многоугольника и их классификация. Получено с: sangakoo.com.
5. Википедия. Декагон. Получено с: es.wikipedia.com.

Мануэль Миер-и-Теран: биография, войны, смерть

Ховард Гарднер: биография, вклад и теория этого психолога