Построить хорду данной окружности равную и параллельную данному отрезку

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Ваш ответ

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

решение вопроса

Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,036
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Даны окружности и отрезок постройте хорду

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Постройте хорду данной окружности, равную и параллельную данному отрезку АВ.

Видео:Построение угла, равного данному. 7 класс.Скачать

Ваш ответ

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

решение вопроса

Видео:Построение угла равного данномуСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,921
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Постройте хорду данной окружности, равную и параллельную заданному отрезку.

Докажем сначала, что геометрическое место середин хорд окружности, равных данному отрезку, меньшему диаметра, — окружность, концентрическая данной.

Пусть a — данный отрезок, R — радиус данной окружности с центром O. Построим прямоугольный треугольник по гипотенузе (радиус данной окружности R) и катету (половина данного отрезка a). Радиусом, равным второму катету построенного прямоугольного треугольника, проведём окружность, концентрическую данной. Через произвольную точку M построенной окружности проведём к ней касательную. Пусть A и B — точки её пересечения с данной окружностью. Тогда OM AB, поэтому M — середина AB, а т.к. хорды, равноудаленные от центра окружности, равны, то AB = a.

Обратно, пусть M — середина хорды AB данной окружности и AB = a. Тогда OM — катет прямоугольного треугольника OMA, в котором OA = R и AM = a. Следовательно, точка M лежит на построенной окружности.

Отсюда вытекает следующее построение. Строим произвольную хорду данной окружности с центром O, равную данному отрезку. Радиусом, равным расстоянию от центра данной окружности до этой хорды, проводим окружность с центром O. Через точку O проводим прямую, перпендикулярную данному отрезку. Через точки пересечения этой прямой с построенной окружностью, проводим прямые, параллельные данному отрезку.

Если данный отрезок меньше диаметра окружности, то задача имеет два решения. Если данный отрезок равен диаметру окружности, то задача имеет единственное решение. Если данный отрезок больше диаметра окружности, то задача не имеет решений.

Предположим, что искомая хорда AB построена. Пусть MN — данный отрезок. Тогда при параллельном переносе на вектор (или ) точка A перейдёт в точку B, а данная окружность S — в окружность S₁, проходящую через точку B.

Отсюда вытекает следующий способ построения. Строим образ S₁ данной окружности при параллельном переносе на вектор (или ). Точки пересечения окружностей S и S₁ — концы искомых хорд.

Если окружности S₁ и S не пересекаются, то задача не имеет решений.

Видео:Теорема об отрезках хорд и секущихСкачать

§ 4. Задачи на построение

Окружность

Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением. Мы уже встречались с определениями, например с определением угла, смежных углов, равнобедренного треугольника и т. д. Дадим определение ещё одной геометрической фигуры — окружности.

Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности (рис. 77). Из определения окружности следует, что все радиусы имеют одну и ту же длину.

Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется её диаметром.

На рисунке 78 отрезки АВ и EF — хорды окружности, отрезок CD — диаметр окружности. Очевидно, диаметр окружности в два раза больше её радиуса. Центр окружности является серединой любого диаметра.

Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. На рисунке 79 ALB и АМВ — дуги, ограниченные точками А и В.

Для изображения окружности на чертеже пользуются циркулем (рис. 80).

Чтобы провести окружность на местности, можно воспользоваться верёвкой (рис. 81).

Часть плоскости, ограниченная окружностью, называется кругом (рис. 82).

Построения циркулем и линейкой

Мы уже имели дело с геометрическими построениями: проводили прямые, откладывали отрезки, равные данным, чертили углы, треугольники и другие фигуры. При этом мы пользовались масштабной линейкой, циркулем, транспортиром, чертёжным угольником.

Оказывается, что многие построения можно выполнить с помощью только циркуля и линейки без масштабных делений. Поэтому в геометрии специально выделяют те задачи на построение, которые решаются с помощью только этих двух инструментов.

Что можно делать с их помощью? Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки. С помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку. Выполняя эти несложные операции, мы сможем решить много интересных задач на построение:

построить угол, равный данному;
через данную точку провести прямую, перпендикулярную к данной прямой;
разделить данный отрезок пополам и другие задачи.

Начнём с простой задачи.

На данном луче от его начала отложить отрезок, равный данному.

Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ (рис. 83, а). Затем циркулем построим окружность радиуса АВ с центром О (рис. 83, б). Эта окружность пересечёт луч ОС в некоторой точке D. Отрезок OD — искомый.

Примеры задач на построение

Видео:Окружность данного радиуса, проходящей через две заданные точкиСкачать

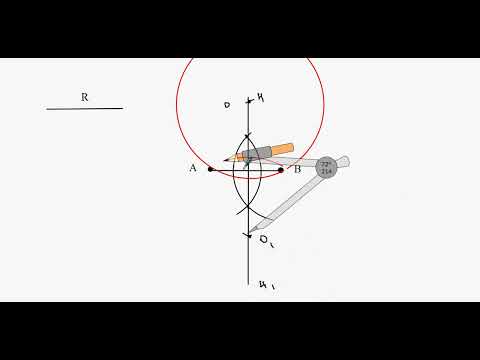
Построение угла, равного данному

Отложить от данного луча угол, равный данному.

Данный угол с вершиной А и луч ОМ изображены на рисунке 84. Требуется построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ.

Проведём окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С (рис. 85, а). Затем проведём окружность того же радиуса с центром в начете данного луча ОМ. Она пересекает луч в точке D (рис. 85, б). После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е. Докажем, что угол МОЕ — искомый.

Рассмотрим треугольники АВС и ODE. Отрезки АВ и АС являются радиусами окружности с центром А, а отрезки OD и ОЕ — радиусами окружности с центром О (см. рис. 85, б). Так как по построению эти окружности имеют равные радиусы, то AB = OD, АС = ОЕ. Также по построению ВС = DE.

Следовательно, ΔАВС = ΔODE по трём сторонам. Поэтому ∠DOE = ∠BAC, т. е. построенный угол МОЕ равен данному углу А.

То же построение можно выполнить и на местности, если вместо циркуля воспользоваться верёвкой.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Построение биссектрисы угла

Построить биссектрису данного угла.

Данный угол ВАС изображён на рисунке 86. Проведём окружность произвольного радиуса с центром в вершине А. Она пересечёт стороны угла в точках В и С.

Затем проведём две окружности одинакового радиуса ВС с центрами в точках В и С (на рисунке изображены лишь части этих окружностей). Они пересекутся в двух точках, из которых хотя бы одна лежит внутри угла. Обозначим её буквой Е. Докажем, что луч АЕ является биссектрисой данного угла ВАС.

Рассмотрим треугольники АСЕ и АВЕ. Они равны по трём сторонам. В самом деле, АЕ — общая сторона; АС и АВ равны как радиусы одной и той же окружности; СЕ = BE по построению.

Из равенства треугольников АСЕ и АВЕ следует, что ∠CAE = ∠BAE, т. е. луч АЕ — биссектриса данного угла ВАС.

Можно ли с помощью циркуля и линейки разделить данный угол на два равных угла? Ясно, что можно, — для этого нужно провести биссектрису этого угла.

Данный угол можно разделить также на четыре равных угла. Для этого нужно разделить его пополам, а затем каждую половину разделить ещё раз пополам.

А можно ли с помощью циркуля и линейки разделить данный угол на три равных угла? Эта задача, получившая название задачи о трисекции угла, в течение многих веков привлекала внимание математиков. Лишь в XIX веке было доказано, что для произвольного угла такое построение невозможно.

Построение перпендикулярных прямых

Даны прямая и точка на ней. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой.

Данная прямая а и данная точка М, принадлежащая этой прямой, изображены на рисунке 87.

На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. Затем построим две окружности с центрами А и В радиуса АВ. Они пересекаются в двух точках: Р и Q.

Проведём прямую через точку М и одну из этих точек, например прямую МР (см. рис. 87), и докажем, что эта прямая — искомая, т. е. что она перпендикулярна к данной прямой а.

В самом деле, так как медиана РМ равнобедренного треугольника РАВ является также высотой, то PM ⊥ а.

Построение середины отрезка

Построить середину данного отрезка.

Пусть АВ — данный отрезок. Построим две окружности с центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. Проведём прямую PQ. Точка О пересечения этой прямой с отрезком АВ и есть искомая середина отрезка АВ.

В самом деле, треугольники APQ и BPQ равны по трём сторонам, поэтому ∠1 =∠2 (рис. 89).

Следовательно, отрезок РО — биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. е. точка О — середина отрезка АВ.

Задачи

143. Какие из отрезков, изображённых на рисунке 90, являются: а) хордами окружности; б) диаметрами окружности; в) радиусами окружности?

144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВС равны; в) ∠BAD = ∠BCD.

145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружности. Найдите ∠POM.

146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, если известно, что СВ = 13 см, АВ = 16 см.

147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВС — диаметр окружности. Докажите, что хорды АВ и АС равны.

148. На прямой даны две точки А и В. На продолжении луча В А отложите отрезок ВС так, чтобы ВС = 2АВ.

149. Даны прямая а, точка В, не лежащая на ней, и отрезок PQ. Постройте точку М на прямой а так, чтобы BM = PQ. Всегда ли задача имеет решение?

150. Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окружности так, чтобы AM = PQ. Всегда ли задача имеет решение?

151. Даны острый угол ВАС и луч XY. Постройте угол YXZ так, чтобы ∠YXZ = 2∠BAC.

152. Дан тупой угол АОВ. Постройте луч ОХ так, чтобы углы ХОА и ХОВ были равными тупыми углами.

153. Даны прямая а и точка М, не лежащая на ней. Постройте прямую, проходящую через точку М и перпендикулярную к прямой а.

Построим окружность с центром в данной точке М, пересекающую данную прямую а в двух точках, которые обозначим буквами А и В (рис. 91). Затем построим две окружности с центрами А и В, проходящие через точку М. Эти окружности пересекаются в точке М и ещё в одной точке, которую обозначим буквой N. Проведём прямую MN и докажем, что эта прямая — искомая, т. е. она перпендикулярна к прямой а.

В самом деле, треугольники AMN и BMN равны по трём сторонам, поэтому ∠1 = ∠2. Отсюда следует, что отрезок МС (С — точка пересечения прямых а и MN) является биссектрисой равнобедренного треугольника АМВ, а значит, и высотой. Таким образом, MN ⊥ АВ, т. е. MN ⊥ а.

154. Дан треугольник АВС. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника. 155. С помощью циркуля и линейки постройте угол, равный: а) 45°; б) 22°30′.

Ответы к задачам

152. Указание. Сначала построить биссектрису угла АОВ.

Видео:Построить угол , равный данному.Скачать

Задачи на построение

Задачи на построение не просты. Не существует единого алгоритма для решения всех таких задач. Каждая из них по-своему уникальна, и каждая требует индивидуального подхода для решения. Именно поэтому научиться решать задачи на по- строение чрезвычайно трудно,а, порой, практически невозможно.

Но эти задачи дают уникальный материал для индивидуального творческого поиска путей решения с помощью своей интуиции и подсознания.

Немного из истории.

Вся история геометрии и некоторых других разделов математики тесно связана с развитием теории геометрических построений. Важнейшие аксиомы геометрии, сформированные Евклидом около 300 года до нашей эры, ясно показывают, какую роль сыграли геометрические построения в формировании геометрии. «От всякой точки до всякой точки можно провести прямую линию», «Ограниченную прямую можно непрерывно продолжать», «Из всякого центра и всяким раствором может быть описан круг» — эти постулаты Евклида явно указывают на основное положение конструктивных методов в геометрии древних.

Древнегреческие математики считали «истинно геометричес- кими лишь построения, производимые циркулем и линейкой, не признавая «законным» использование других средств для решения конструктивных задач». При этом , в соответствии с постулатами Евклида, они рассматривали линейку как неограни- ченную и одностороннюю, а циркулю приписывалось свойство чертить окружности любых размеров. Эта традиция до сих пор сохранилась в школьном курсе геометрии.

Древнегреческие геометры успешно справлялись с труднейшими задачами на построение с помощью циркуля и линейки. Так, например, Аполлоний Пергский решил известную задачу, носящую его имя : «Построить окружность, касающую- ся трех данных окужносей».

В XVII – XX веках теория геометрических построений стала развиваться дальше, главным образом, в связи с созданием новых разделов математики.

Много внимания уделяли конструктивным задачам творцы современной математики : Декарт, Ферма, Ньютон, Паскаль, Эйлер, Гаусс и другие.

В XVII – XIX веках разрабатывается теория геометрических построений с помощью различных инструментов, отличных от принятых древними. Уже Леонардо да Винчи ( 1452 – 1519 г. г. ) рассматривал построения с помощью линейки и циркуля посто- янного размаха. Датчанин Мор ( 1672 г. ) и итальянец Маскерони

( 1797 г. ) изучали построения, выполняемые циркулем и линей- кой. Швейцарец Ламберт ( 1774 г. ) рассматривал некоторые за- дачи на построение на ограниченном куске плоскости.

В настоящее время теория геометрических построений представляет обширную и глубоко развитую область математи- ки, связанную с решением разнообразных принципиальных вопросов, уходящих в другие ветви математики.

Существование центра окружности, вписанной в треугольник; существование подобных треугольников; существование парал- лельных прямых доказывается с помощью построен.

Что такое задачи на построение?

Основные методы решения.

Задача на построение в планиметрии состоит в том, чтобы, исходя из заданных на плоскости геометрических фигур, применяя заранее предписанные средства (инструменты), построить новую геометрическую фигуру, находящуюся в определенных отношениях с данными фигурами. В качестве средств построения выступают либо классические инструменты – циркуль и линейка, либо ограниченные средства построения – угольник (математическая модель прямого угла); линейка с параллельными краями, или другие средства.

В решении задач на построение выделяются следующие четыре этапа: 1. АНАЛИЗ

В процессе анализа , собственно и происходит поиск решения задачи. Из предположения, что задача уже решена и требуемая фигура построена, пытаются вывести такие следствия, которых окажется достаточно для того, чтобы требуемую фигуру построить.

Построение предлагает поэтапное выполнение построений с помощью циркуля и линейки, в результате которых получаем требуемую фигуру.

В доказательстве поясняем, что построенная фигура действительно удовлетворяет всем требованиям задачи.

Наконец, в исследовании нужно установить, при каком выборе исходных данных задача имеет решение и сколько решений будет при каждом допустимом выборе исходных данных.

Отметим простейшие построения, которые служат основой для выполнения других, более сложных.

1. Построить отрезок, равный данному.

2. Построить угол, равный данному.

3. Разделить данный отрезок пополам.

4. Разделить данный угол пополам.

5. Через данную точку провести прямую, параллельную данной прямой.

6. Из данной точки, не принадлежащей данной прямой, опустить на эту прямую перпендикуляр.

7. Из данной точки, лежащей на прямой, восстановить к этой прямой перпендикуляр.

8. Построить треугольник по трем сторонам ( т. е. построить треугольник, стороны которого были бы равны трем заданным отрезкам ).

9. Построить треугольник по двум сторонам и заключенному между ними углу ( т. е. построить треугольник, две стороны которого и угол, заключенный между ними, были бы равны двум заданным отрезкам и заданному углу соответственно ).

В решении задач на построение часто используются различные методы геометрического преобразования плоскости :

— метод геометрических мест;

— метод центральной и осевой симметрии;

— метод параллельного перенесения;

— алгебраический метод и др.

Каждому методу сопоставляется определенный класс задач. Однако провести классификацию задач на построение по методам их решения нельзя. Это следует уже из того, что многие задачи допускают несколько методов решения. Поэтому можно говорить лишь об условном разбиении задач на построение на классы, определяемые их методами решения.

В данной работе рассмотрены некоторые из этих методов и задачи, решаемые с их помощью.

Примеры решения задач на построение с использованием различных методов.

Даны две концентрические окружности О и точка А на большей окружности. Провести секущую AXYZ так, чтобы AZ = 3XY.

1. Анализ исходных данных:

Пусть ОВXY ; AB = BZ ; XB = BY AB = 3XB

Откуда AX = 2BX AX = XY.

Для определения т. Y проведем диаметр АС и соединим точки С и Y.

AOXACY ( АО = ОС ; AX = XY ) YC = 2OX.

Значит т. Y принадлежит окр. ( C ; MN ).

2. окр. ( C ; MN ) окр. ( O ; OM ) = т. Y

4. секущая AY – искомая.

1. AOX ACY ( AC : AO =

2. AX = XY AZ = 3XY.

4. Исследование решения:

Если MN = NC – одно решение

Если MN NC – два решения ( секущие AY и AY );

Если MN NC – решений нет.

Через точку А провести прямую , проходящую между данными точками

В и С и находящуюся от них на равном расстоянии.

1. Анализ исходных данных:

Пусть искомая прямая АВ построена, такая, что ML = BC.

Так как прямая определяется двумя точками, и одна из них известна (т. А), необходимо найти на искомой прямой вторую точку. Соединим точки В и С.

LMO = OBC OL = OC (как соответствующие элементы) т. О – середина LC.

1. LM AB (элементарное построение).

2. СВ АВ (элементарное построение).

6. АО – искомая прямая.

(по гипотенузе и острому углу).

Задача всегда имеет решение.

Если т. А LC и т. А не совпадает с т. О, то искомая прямая совпадает с LC.

Если т. А совпадает с т. О , то всякая прямая , проходящая через т. О, будет искомая.

Через точку А провести прямую так, чтобы ее отрезок между параллельны- ми прямыми MN и PQ был равен данному отрезку а.

1. Анализ исходных данных:

Пусть прямая АС проведена через точку А так, что ВС = а. Задача сводится к определению ACR. Проведем через произвольную точку Е PQ отрезок DE AC, тогда DE = a, и все такие же отрезки будут равны а.

Так как DE = a , то точка D окр. ( Е ; а ).

= т. D окр. (Е ; а) MN =

4. т. А а ;a ED т. А а ; а EK

6. BC и SR – искомые.

1. BC = DE ; SR = EK

(как отрезки между прямыми)

2. DE = EK = a ( окр. r = a )

3. BC = SR = a – искомые.

Задача вообще имеет два решения.

При а = MP – одно решение, искомая прямая MN

При а MP – решений нет.

Через данную точку М провести окружность , касательную к данной окружности О в данной на ней точке L.

1. Анализ исходных данных:

Пусть окружность с центром О — искомая. Найдем центр О. Так как точка касания двух окружностей лежит на одной прямой с их центрами , то О OL. Соединим точки M и L. LM – хорда искомой окружности центр О PQ, где PQ ML ( по свойству радиуса ).

Окончательно, OL PQ = O.

6. r = ОМ – искомый радиус

7. окр. ( О ; ОМ ) – искомая окружность.

1. О L = OM (как наклонные, имеющие равные проекции) т. L и т. М окр. (О; ОМ)

2. окр. О окр. О = т. L (так как расстояние между центрами равно сумме радиусов).

Если т. М дана внутри окружности О ,то решение остается то же, но касание окружностей будет внутреннее и расстояние между центрами равно разности радиусов.

Если т. М находится на окружности О, то искомая окружность совпадает с данной.

Если т. М лежит на касательной ML , то решений нет , так как перпендикуляр PQ OL и точки пересечения нет.

Должно выполняться условие:

Даны окружность О и точка А вне ее ; через точку А провести секущую так, чтобы она окружностью разделилась пополам.

1. Анализ исходных данных.

Пусть секущая АВ проведена так, что АС = СВ. Необходимо определить точку В. Проведем d = BD. Соединим точку D с точками А и С.

DCB = 90; DAC = DCB т. D принадлежит окр. ( А ; MN ).

1. окр. ( А ; MN ) ; т. D окр. О

2. соединим точки D и О

4. DO окр. ( А ; MN ) = т. В

5. соединим точки В и А

6. ВА – искомая секущая.

1. DCB = 90 ( опирается на диаметр ).

( СD-общий ; АС = СВ по условию ) AD = DB

4. ADB – равнобедренный ( r – стороны )

5. DC – высота ADB ( также биссектриса и медиана )

Если окружность ( А ; 2r ) пересекает окружность О, то решения два ( секущие АВ и AL ).

Если окружность ( А ; 2r ) касается окружности О , то решение одно

Если окружность DK, описанная из т. А, не пересекает окружность О , то решений нет.

Условие существования решения : AO 3r

МЕТОД ГЕОМЕТРИЧЕСКИХ МЕСТ.

Геометрическое место точек – совокупность точек, обладающих свойствами, исключительно им принадлежащими. При решении задач на построение наиболее часто встречаются следующие геометрические места точек, которым удовлетворяют искомые фигуры:

1. Множество точек плоскости, каждая из которых равноудалена от двух данных точек А и В, есть серединный перпендикуляр отрезка АВ.

2. Множество точек, находящихся на данном расстоянии от данной пря- мой, есть две прямые, параллельные данной и отстоящие от нее на дан- ном расстоянии.

3. Множество точек, каждая из которых равноудалена от двух данных па- раллельных прямых, есть прямая, являющаяся их осью симметрии.

4. Множество точек, каждая из которых равноудалена от двух пересекаю- щихся прямых, есть две взаимно – перпендикулярные прямые, содер- жащие биссектрисы углов, образованных данными прямыми.

5. Множество точек, из которых отрезок АВ виден под прямым углом, есть окружность ( без точек А и В ), построенная на отрезке АВ как на диаметре.

6. Множество точек плоскости, из которых отрезок АВ виден под углом

; , есть две дуги с общими концами А и В ( без точек А и В ), симметричные относительно прямой АВ.

7. Множество точек на плоскости, для каждой из которых отношение рас- стояний до двух данных точек А и В постоянно и отлично от единицы, есть окружность с центром на прямой АВ. Эта окружность называется окружностью Апполония.

Найти точку Х, равноудаленную от всех трех вершин данного треуголь- ника АВС.

1. Анализ исходных данных:

Пусть искомая точка X найдена так, что XB = XC т. X принадлежит серединному перпендикуляру MN, также т. X принадлежит серединному перпендикуляру PQ т. Х лежит на пересечении серединных перпендикуляров MN, PQ и KL.

1. М – середина АВ

2. К – середина ВС

3. Р – середина АС

7. KL MN = т. Х – искомая

1. серединные перпендикуляры пересекаются в одной точке Х — центре описанной окружности окр. ( Х ; ХА ).

2. ХА = ХВ = ХС = r

Если АВС остроугольный или прямоугольный , т. Х лежит внутри него.

Если АВС тупоугольный, т. Х лежит вне его.

Построить ромб так, чтобы одна из его диагоналей была равна данному отрезку m и лежала на данной прямой а, а остальные две вершины ромба лежали соответственно на данных прямых b и с.

1. Анализ исходных данных:

Пусть АВСD – искомый ромб, АD = m. Точки В и С симметричны относительно а ( по свойству диагоналей ромба ). Точка В лежит на прямой b, точка С – на прямой с ( по условию ), но прямая в симметрична прямой b относительно прямой а, значит точка С лежит на пересечении прямых с и b.

1. а, b, с – данные прямые ;

3. ММа = т. Р ; МР =РМ

5. NNа = т. Q ; NQ = QN

9. СВ а = т. О ; СО = ОВ

11. Аа ; Da ; ОА =ОD = m/2

12. АВDC – искомый ромб.

1. СО = ОВ = m/2 ( по построению)

2. АО = ОD = m/2 ( по построению)

3. СВа ( по построению )

4. ADa CB AD ( диагонали ромба )

Если с b — решений нет.

Если с совпадает с b — решений бесконечно много.

Если с и b пересекаются на прямой а – решений нет.

Построить ромб по стороне а и радиусу вписанной окружности b.

1. Анализ исходных данных:

Пусть ромб ABCD построен так, что AB = BC = CD = DA = a и радиус вписанной окружности ОМ = b. Точка О является вершиной прямого угла, опирающегося на АВ, и находится на расстоянии b от АВ.

2. К – середина АВ

1. ABCD – ромб со стороной а ( по построению )

2. Пусть ОМ АВ ОМ = ЕК = b ( ОМ EK ; AB d – как параллельные прямые между параллельными )

3. окр. ( О ; ОМ ) касается АВ

4. т. О – центр симметрии ( по свойству диагоналей ромба )

5. окр ( О ; ОМ ) касается всех сторон ромба является вписанной.

Задача имеет решение, если прямая d пересекает окружноcть ( К ; АК ), то есть когда b a/2.

Даны два отрезка MN и PQ ; на одной прямой АВ найти такую точку Х , чтобы MXN и PXQ были равновелики.

1. Анализ исходных данных:

Пусть точка Х найдена так, что она лежит на прямой АВ и MXN равнове- лик PXQ. Если XZ и XY высоты этих треугольников, то

XZ : XY = PQ : MN ( высоты треугольников обратно пропорциональны соответствующим сторонам ), значит точка Х находится на геометрическом месте точек на расстоянии, равном данному отношению PQ : MN, а также – на прямой АВ.

5. OS = MN ; OR = PQ

6. из т. S проведем SS PQ

7. из т. R проведем RR MN

9. СО АВ = т. Х – искомая

1. OYX OKC — по двум углам (О и 90) XY/CK = OX/OC

2. OXZ OCL — по двум углам (O и 90) XZ/CL = OX/OC

4. Заменим CK = OS = MN ; CL = OR =PQ XY/MN = XZ/PQ

5. XY x PQ = MN x XZ ( из определения пропорции )

6. Разделим оба произведения на 2:

S MXN = S PXQ = 1/2 XY x PQ = 1/2 MN x XZ

Задача имеет одно решение.

Если MN PQ , то OS OR , следовательно нет точки пересечения , и задача решений не имеет.

Условия задач, решаемых методом подобия дают возможность построить не искомую фигуру, а фигуру, подобную искомой. Затем из множества подобных фигур выбрать одну, удовлетворяющую условиям задачи либо только по своим размерам, либо по своему положению и своим размерам.

Построить треугольник, зная сторону а, сторону b, вершину В и радиус вписанной окружности r.

1. Анализ исходных данных:

Пусть треугольник АВС построен так, что известны угол и отношение сторон этого угла. Построим треугольник, подобный искомому.

1. х –единичный отрезок.

2. на сторонах В отложим BD = mx

3. соединим D и E

4. DBE ABC – по двум углам

( при вершине и при основании )

5. BP – биссектриса В

6. OF DE прямая а

7. на прямой а отложим OG = r

8. через т. G проводим АС DE

Из всех подобных треугольников

АВС искомый , так как радиус вписанной окружности равен r, что следует из построения.

Всегда возможно одно решение.

Дан угол АВС и внутри его точка М. Найти на стороне ВС точку Х , равноудаленную от АВ и от точки М.

1. Анализ исходных данных:

Пусть точка Х найдена так, что перпендикуляр XY = MN. Задача сводится к построению фигуры YXM. Представим целый ряд фигур abc; pmn,, гомотетических с искомой фигурой. Достаточно построить одну из этих фигур, например, abc, тогда останется провести из точки М параллель bc, и задача будет решена.

1. точки М, b, m, В ВМ ( т. В – центр подобия искомых фигур )

2. положение т. а произвольно ас АВ ; ас = bc

3. из центра с опишем дугу аk ( с ; ас )

4. дуга ak ВМ = т. b

5. проводим MX bc

6. MX BC = т. X ( искомая )

1. опустим XY АВ

2. abc YMX (равные углы между пропорциональными сторонами)

4. cb = ca ( по построению – дуга ak ) X M = XY

Задача всегда имеет два решения , так как дуга ak из центра с пересекает прямую ВМ в двух точках.

Предполагают задачу решенной и одну из данных точек ( прямую или окружность ) отражают относительно какой – нибудь известной оси ; иногда эта ось проходит через известную точку. И полученную симметричную точку ( прямую или окружность ) подчиняют тем же условиям, которым должна была удовлетворять замененная.

На данной прямой АВ найти точку Х, соединив которую с данными точками M и N, получим углы NXB (1) и MXK, из которых один вдвое больше другого.

1. Анализ исходных данных:

Пусть точка Х найдена так, что 1 = 2MXK , и точка С симметрична точке М относительно прямой АВ. Тогда 2 = 3, и задача сводится к нахождению на прямой АВ точки Х такой, чтобы 1 = 23.

1. т. С симметрична т. М относительно АВ

4. NK – касательная к окр. ( С ; LC )

3. LXC = CXK — ( УСУ )

— биссектриса LXK NX – касательная к окр. ( С ; LC )

5. 1 = LXK ; 3 = MXA NXB = 2MXA.

Задача имеет четыре решения, если точки M и N расположены вне прямой АВ, так как из каждой точки к окружности можно провести две касательные.

Дан угол ВАС и точка P внутри него. Построить окружность, проходящую через точку Р и касающуюся сторон угла.

1. Анализ исходных данных:

Пусть окружность О построена так, что проходит через данную точку Р и касается сторон АВ и АС данного угла в точках M и N. Центр О лежит на биссектрисе l данного угла , а точка Р симметрична точке Р относительно l и лежит на окружности. Пусть прямая РР пересекает одну из сторон угла в точке Q. Тогда QM является отрезком касательной к окружности, поэтому

QM= QP x QP. Построив точку М, легко построить точку О.

1. l – биссектриса ВАС

3. PP l = т. Т ; РТ = ТР

5. x = x ( среднее геометрическое )

6. т. М АВ ; х = QM

7. т. М АВ ; х = QM

1. АОМ АОМ- по двум углам ( А – обший;

2. АОN AON- по острому А

3. OM = OP окр. ( О; ОМ) проходит через т. Р и касается сторон угла.

Очевидно, что если точка Р лежит строго внутри заданного угла, то задача имеет ровно два решения. В процессе решения использовались элементы нескольких методов: геометрического места точек, осевой симметрии и алгебраического метода.

Метод состоит в том, что некоторую ломаную линию в чертеже заменяют прямой. После решения новой задачи определяют, в какой точке нужно согнуть выпрямленную линию , и таким образом перейти к первоначальной задаче. Особенно этот метод применим в тех задачах, условия которых содержат данную сумму или разность частей некоторой ломаной линии.

Построить треугольник, зная угол А, сторону с и сумму двух других сторон а + b.

1. Анализ исходных данных.

Пусть АВС построен так, что сумма звеньев ломаной ВСА известна. Выпрямим ее. Для этого откладываем на продолжении АС часть СD = BC.

Соединяем точки В и D. ВCD – равнобедренный вершина С лежит на серединном перпендикуляре ЕС ( по свойству медианы равнобедренного ).

2. АВ = c ; АD = a + b

1. А ; АВ – известны по условию

2. ВС + АС = CD + AC = a + b

Построение возможно, если a + b > c

Построить равнобедренный треугольник, зная его боковую сторону а и сумму высоты и основания, равную S.

1. Анализ исходных данных:

Пусть АВС построен так, что АВ =ВС =а ; ВD = AC = S. Необходимо определить точку А. Введем данную сумму в чертеж. Для этого отложим на продолжении BD отрезок DE = AC, значит DE = 2AD (т. к. BD еще и медиана), то есть вид ADE известен. Если в AED произвольно провести

GF AD , то FE = 2 GF ( по т. Фалеса ).

5. дуга ( В ; а ) EG = т. А

7. дуга ( В ; а ) AD = т. С

1. АВ = ВС – радиус окр. ( В ; ВС )

2. AD EB (по построению ) BD – высота АВС

3. дуга АС стягивает хорду AC;

BD – медиана АВС

4. АВС – равнобедренный.

Решение существует, если АВ ВК.

Построить треугольник по периметру Р и двум углам, величины которых равны и.

1. Анализ исходных данных:

Пусть АВС – искомый, в котором АВ + ВС + СА = Р ; ВАС = ; ВСА =. На продолжении СА отложим отрезок СЕ = СВ, а на продолжении АС – отрезок СЕ = СВ, тогда длина отрезка DE = P.

Соединим точки D и Е с вершиной В, получим два равнобедренных треугольника : DBA и ЕВС, в которых ADB = ABD = /2 ;

5. DBE – вспомогательный.

6. т. К – середина DB

7. KA DB ; КА DE = т. А

8. т. N – середина ВЕ

9. NC BE ; NC DE = т. С

10. АВС – искомый.

1. DAB – равнобедренный ( т. к. КА – медиана и высота )

2. ВАС = /2 х 2 = А ( по теореме о внешнем угле )

4. Аналогично: ВСА = ; ЕС = СВ

5. ВА + АС + СВ = Р ( по аксиоме об измерении отрезков )

💥 Видео

Построение касательных | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Деление окружностиСкачать

11 класс, 40 урок, Угол между касательной и хордойСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

#234. Формула Эйлера | Свойства отрезков хорд и секущихСкачать

Задача на нахождение длины хорды окружностиСкачать