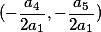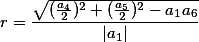| Три точки по которым необходимо построить окружность |
| Первая координата |
| Вторая координата |
| Третья координата |
| Полученная формула окружности |
Напомним, что общее уравнение кривой второго порядка выглядит так
Частные примеры кривой второго порядка это и парабола и гибербола и окружность и прямая линия.
Формула окружности с центром (a;b) и радиусом R имеет вид
или если мы раскроем скобки
из этого уравнения мы можем видеть что кривая второго порядка превращается в формулу окружности если
Из этого же мы можем утверждать, что для построения окружности нам нужно как минимум три точки, так как у нас из всех шести вышеуказанных коэффициентов, только три коэффицента неизвестны.
Бот, позволяет Вам рассчитывать формулу окружности по заданным трем точкам.
Если бы бота не было, то Вам пришлось бы решать систему уравнений из трех переменных, что не очень удобно и трудоёмко.
- Интересные факты
- Синтаксис
- Примеры
- Уравнение окружности, проходящей через три заданные точки
- Уравнение окружности, проходящей через три заданные точки
- Первая точка
- Вторая точка
- Третья точка
- Центр
- Как найти окружность, проходящюю через три заданные точки
- Уравнение окружности по трем точкам
- Уравнение окружности
- Пример
- Решение :
- Шаг :2
- Шаг :3
- Шаг :4
- Шаг :5
- 📺 Видео
Видео:Построение окружности по трём точкам.Скачать

Интересные факты
Если Вам известны все коэффициенты кривой второго порядка , которые выражают окружность ( ), то очень легко по ним определить два основных параметра:центр окружности и радиус окружности
Центр окружности
Радиус окружности
Видео:Построение окружности по трем точкамСкачать

Синтаксис
Так как это частный пример уже созданного бота то просто расскажем о нюансах
kp2 1 1 0 координаты точек
Где координаты точек есть представление в виде x:y (х-абсцисса, y-ордината)
Каждая координата точки, должна разделятся как минимум одним пробелом.
Что же такое 1 1 0 ? Это уже известные нам коэффициенты при общей формуле.
Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Примеры
Составить уравнение окружности, проходящей через точки (3,1) (-2,6) и (-5,-3)
Так и запишем kp2 1 1 0 3:1 -2:6 -5:-3
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Уравнение окружности, проходящей через три заданные точки
Этот онлайн калькулятор выводит уравнение окружности, проходящей через три заданные точки
Этот онлайн-калькулятор находит окружность, проходящую через три заданные точки. Калькулятор находит центр, радиус и уравнение окружности, и строит окружность на графике. Методы, использованные для нахождения центра и радиуса окружности, описаны ниже под калькулятором.
Уравнение окружности, проходящей через три заданные точки
Первая точка
Вторая точка
Третья точка
Центр
Видео:Уравнение окружности (1)Скачать

Как найти окружность, проходящюю через три заданные точки
Давайте вспомним как выглядит уравнение окружности в стандартной форме:
Так как все три точки принадлежат одной окружности, мы можем записать систему уравнений
Значения , и мы знаем. Давайте сделаем подстановку с неизвестными переменнами a, b и c.
Теперь у нас есть три линейных уравнения для трех неизвестных — составим систему уравнений соответствующую матричной форме:
Мы можем решить эту систему уравнений, используя, к примеру, Гауссово исключение. (подробнее прочитать об этом можно здесь — Решение системы линейных алгебраических уравнений методом Гаусса ). «Нет решений» — означает, что точки коллинеарны и окружность через них провести нельзя.
Координаты центра окружность и ее радиус относится к подобному решению
Зная центр и радиус, мы можем получить уравнение окружности, используя этот калькулятор — Уравнение окружности по заданному центру и радиусу в различных формах
Видео:Как искать точки на тригонометрической окружности.Скачать

Уравнение окружности по трем точкам
Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.
Уравнение окружности
r 2 = (x — h) 2 + (y — k) 2
- h,k — координаты центра Окружности
- x,y — координаты точки окружности
- r — радиус
Пример
Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)
Решение :
Подставляем координаты точек в формулу
- (2 — h) 2 + (2 — k) 2 = r 2
- (2 — h) 2 + (4 — k) 2 = r 2
- (5 — h) 2 + (5 — k) 2 = r 2
Шаг :2
Найдем значение k упрощая 1 и 2 уравнения
- (2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
- 4 — 4h + h 2 + 4 — 4k + k 2 = 4 — 4h + h 2 +16 — 8k + k 2
- 8 — 4k = 20 — 8k
- k= 3
Шаг :3
Найдем значение h упрощая уравнения 2 и 3
- (2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
- 4 — 4h + h 2 + 4 — 4k + k 2 = 25 — 10h + h 2 + 25 — 10k + k 2
- 8 — 4k — 4h = 50 — 10h — 10k
- 6k + 6h = 42
Подставив значение k=3 в уравнение
Получаем координаты точки центра (h,k) = ( 4,3 )
Шаг :4
Подставим значения h,k в формулу
- r 2 = (x — h) 2 + (y — k) 2
- r 2 = (2 — 4) 2 + (2 — 3) 2
- r 2 = (-2) 2 + (-1) 2
- r 2 = 5
- r = 2.24
Шаг :5
Подставим значения h, k в уравнение окружности
(x — h) 2 + (y — k) 2
Уравнение окружности = (x — 4) 2 + (y — 3) 2
📺 Видео
Построение окружности по 3 точкамСкачать
Математика. Центр окружности по трем точкамСкачать

Видеоурок "Уравнение плоскости по трем точкам"Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение окружности и формула расстояния между точками на плоскостиСкачать

10 класс, 11 урок, Числовая окружностьСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Уравнение плоскости через 3 точкиСкачать

Нахождение центра окружности по 3-м точкам в AutoCADСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать