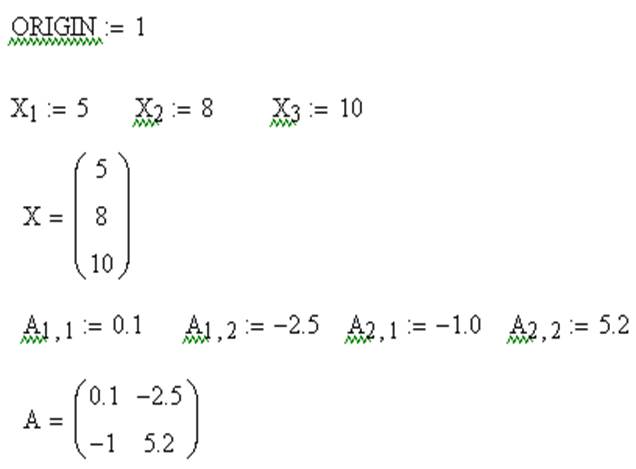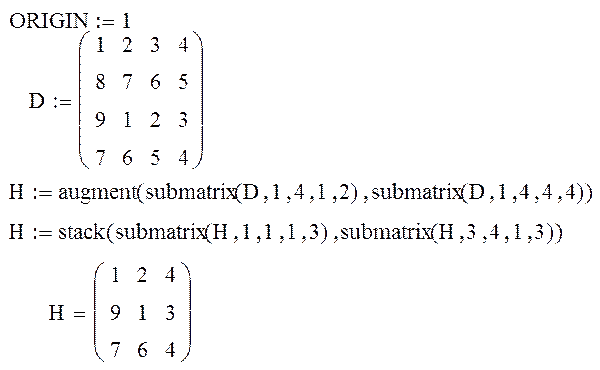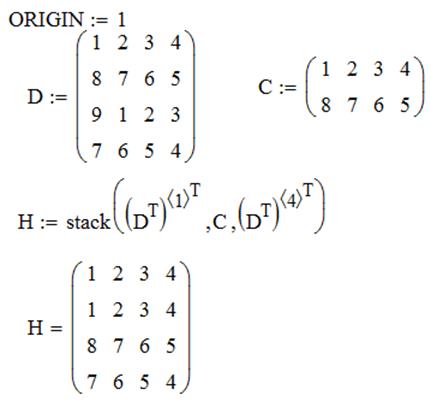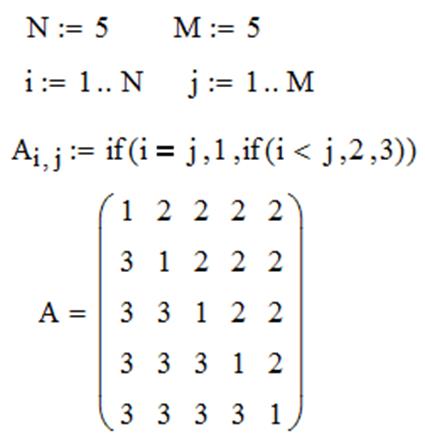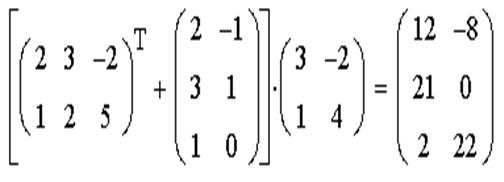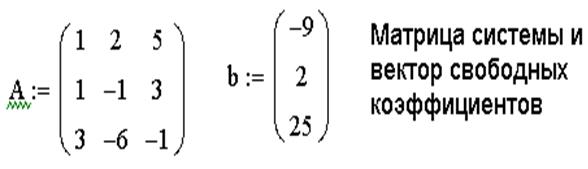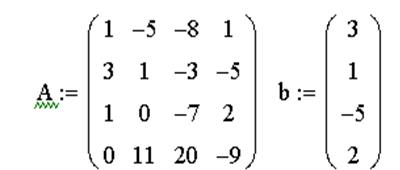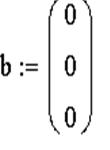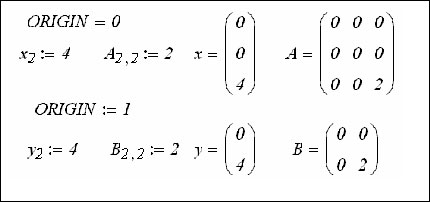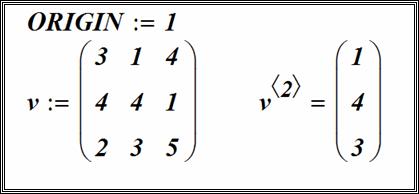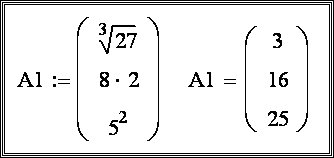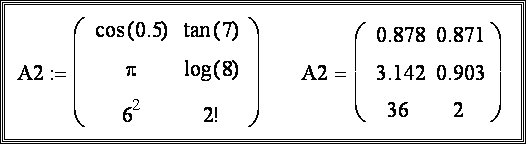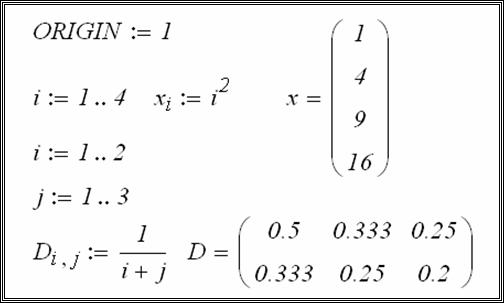Mathcad содержит функции для обычных в линейной алгебре действий с массивами. Эти функции предназначены для использования с векторами и матрицами. Если явно не указано, что функция определена для векторного или матричного аргумента, не следует в ней использовать массивы как аргумент. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.
Если Вы используете Mathcad PLUS, Вы будете также иметь несколько дополнительных функций, определенных для векторов. Эти функции скорее предназначены для анализа данных, чем для действий с матрицами. Они обсуждены в Главе “Встроенные функции”.
Следующие таблицы перечисляют векторные и матричные функции Mathcad. В этих таблицах
- A и B — массивы (векторы или матрицы).
- v — вектор.
- M и N — квадратные матрицы.
- z — скалярное выражение.
- Имена, начинающиеся с букв m, n, i или j — целые числа.
Размеры и диапазон значений массива
В Mathcad есть несколько функций, которые возвращают информацию относительно размеров массива и диапазона его элементов. Рисунок 10 показывает, как эти функции используются.
| Имя функции | Возвращается. |
| rows(A) | Число строк в массиве A. Если А — скаляр, возвращается 0. |
| cols(A) | Число столбцов в массиве A. Если A скаляр, возвращается 0. |
| length(v) | Число элементов в векторе v. |
| last(v) | Индекс последнего элемента в векторе v. |
| max(A) | Самый большой элемент в массиве A. Если A имеет комплексные элементы, возвращает наибольшую вещественную часть плюс i, умноженную на наибольшую мнимую часть. |
| min(A) | Самый маленький элемент в массиве A. Если A имеет комплексные элементы, возвращает наименьшую вещественную часть плюс i, умноженную на наименьшую мнимую часть. |
Рисунок 10: Векторные и матричные функции для нахождения размера массива и получения информации относительно диапазона элементов.
Специальные типы матриц
Можно использовать следующие функции, чтобы произвести от массива или скаляра матрицу специального типа или формы. Функции rref, diag и geninv доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| identity(n) | n x n единичная матрица (матрица, все диагональные элементы которой равны 1, а все остальные элементы равны 0). |
| Re(A) | Массив, состоящий из элементов, которые являются вещественными частями элементов A. |
| Im(A) | Массив, состоящий из элементов, которые являются мнимыми частями элементов A. |
| Е diag(v) | Диагональная матрица, содержащая на диагонали элементы v. |
| Е geninv(A) | Левая обратная к A матрица L такая, что L A = I, где I — единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А — m x n вещественная матрица, где m>=n. A = I, где I — единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А — m x n вещественная матрица, где m>=n. |
| Е rref(A) | Ступенчатая форма матрицы A. |
Рисунок 11: Функции для преобразования массивов. Обратите внимание, что функции diag и rref являются доступными только в Mathcad PLUS.
Специальные характеристики матрицы
Можно использовать функции из следующей таблицы, чтобы найти след, ранг, нормы и числа обусловленности матрицы. Кроме tr, все эти функции доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| tr(M) | Сумма диагональных элементов, называемая следом M. |
| Е rank(A) | Ранг вещественной матрицы A. |
| Е norm1(M) | L1 норма матрицы M. |
| Е norm2(M) | L2 норма матрицы M. |
| Е norme(M) | Евклидова норма матрицы M. |
| Е normi(M) | Равномерная норма матрицы M. |
| Е cond1(M) | Число обусловленности матрицы M, основанное на L1 норме. |
| Е cond2(M) | Число обусловленности матрицы M, основанное на L2 норме. |
| Е conde(M) | Число обусловленности матрицы M, основанное на евклидовой норме. |
| Е condi (M) | Число обусловленности матрицы M, основанное на равномерной норме. |
Формирование новых матриц из существующих
В Mathcad есть две функции для объединения матриц вместе — бок о бок, или одна над другой. В Mathcad также есть функция для извлечения подматрицы. Рисунки 12 и 13 показывают некоторые примеры.
| Имя функции | Возвращается. |
| augment (A, B) | Массив, сформированный расположением A и B бок о бок. Массивы A и B должны иметь одинаковое число строк. |
| stack (A, B) | Массив, сформированный расположением A над B. Массивы A и B должны иметь одинаковое число столбцов. |
| submatrix (A, ir, jr, ic, jc) | Субматрица, состоящая из всех элементов, содержащихся в строках с ir по jc и столбцах с ic по jc. Чтобы поддерживать порядок строк и-или столбцов, удостоверьтесь, что ir |
Рисунок 12: Объединение матриц функциями stack и augment.
Рисунок 13: Извлечение субматрицы из матрицы при помощи функции submatrix.
Собственные значения и собственные векторы
В Mathcad существуют функции eigenval и eigenvec для нахождения собственных значений и собственных векторов матрицы. В Mathcad PLUS также есть функция eigenvecs для получения всех собственных векторов сразу. Если Вы используете Mathcad PLUS, Вы будете также иметь доступ к genvals и genvecs для нахождения обобщенных собственных значений и собственных векторов. Рисунок 14 показывает, как некоторые из этих функций используются.
| Имя функции | |
| eigenvals (M) | Вектор, содержащий собственные значения матрицы M. |
| eigenvec (M, z) | Матрица, содержащая нормированный собственный вектор, соответствующий собственному значению z квадратной матрицы M. |
| Е eigenvecs (M) | Матрица, содержащая нормированные собственные векторы, соответствующие собственным значениям квадратной матрицы M. n-ный столбец возвращенной матрицы — собственный вектор, соответствующий n-ному собственному значению, возвращенному eigenvals. |
| Е genvals (M,N) | Вектор v собственных значений, каждое из которых удовлетворяет обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. Вектор x — соответствующий собственный вектор. |
| Е genvecs (M,N) | Матрица, содержащая нормализованные собственные векторы, соответствующие собственным значениям в v, векторе, возвращенном genvals. n-ный столбец этой матрицы — собственный вектор x, удовлетворяющий обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. |
Рисунок 14: Нахождение собственных значений и собственных векторов.
Рисунок 15: Использование eigenvecs для одновременного нахождения всех собственных векторов.
Если Вы используете Mathcad PLUS, Вы будете иметь доступ к некоторым дополнительным функциям для выполнения специальных разложений матрицы: QR, LU, Холесского, и по сингулярным базисам. Некоторые из этих функций возвращают две или три матрицы, соединенные вместе в одну большую матрицу. Используйте submatrix, чтобы извлечь эти две или три меньшие матрицы. Рисунок 16 показывает пример.
| Имя функции | Возвращается. |
| Е cholesky(M) | Нижняя треугольная матрица L такая, что L L T =M. Матрица M должна быть симметричной положительно определенной. Симметрия означает, что M=M T , положительная определённость — что x T L T =M. Матрица M должна быть симметричной положительно определенной. Симметрия означает, что M=M T , положительная определённость — что x T  M M x>0 для любого вектора x x>0 для любого вектора x  0. 0. |
| Е qr(A) | Матрица, чьи первые n столбцов содержат ортогональную матрицу Q, а последующие столбцы содержат верхнюю треугольную матрицу R. Матрицы Q и R удовлетворяют равенству A=Q R. Матрица A должна быть вещественной. R. Матрица A должна быть вещественной. |
| Е lu(M) | Матрица, которая содержит три квадратные матрицы P, L и U, расположенные последовательно в указанном порядке и имеющие с M одинаковый размер. L и U являются соответственно нижней и верхней треугольными матрицами. Эти три матрицы удовлетворяют равенству P M=L M=L U . U . |
| Е svd(A) | Матрица, содержащая две расположенные друг над другом матрицы U и V. Сверху находится U — размера m x n, снизу V — размера n x n. Матрицы U и V удовлетворяют равенству A=U diag(s) diag(s) V T , где s — вектор, возвращенный svds(A). A должна быть вещественнозначной матрицей размера m x n, где m>=n. V T , где s — вектор, возвращенный svds(A). A должна быть вещественнозначной матрицей размера m x n, где m>=n. |
| Е svds(A) | Вектор, содержащий сингулярные значения вещественнозначной матрицы размера m x n, где m>=n. |
Рисунок 16: Использование функции submatrix для извлечения результата из функции rq. Используйте submatrix, чтобы извлечь подобным образом результаты из функций lu и svd. Обратите внимание, что эти функции доступны только в Mathcad PLUS.
Решение линейной системы уравнений
Если Вы используете Mathcad PLUS, Вы сможете использовать функцию lsolve для решения линейной системы уравнений. Рисунок 17 показывает пример. Обратите внимание, что M не может быть ни вырожденной, ни почти вырожденной для использования с lsolve. Матрица называется вырожденной, если её детерминант равен нулю. Матрица почти вырождена, если у неё большое число обусловленности. Можно использовать одну из функций, описанных на странице 204, чтобы найти число обусловленности матрицы.
| Имя функции | |
| Е lsolve (M, v) | Вектор решения x такой, что M x=v. x=v. |
Если Вы не используете Mathcad PLUS, Вы всё-таки можете решать систему линейных уравнений, используя обращение матрицы, как показано в нижнем правом углу Рисунка 9.
Рисунок 17: Использование lsolve для решения системы из двух уравнений с двумя неизвестными.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:Урок 8. МКЭ в Mathcad. Векторы концевых усилийСкачать

Векторы и матрицы в MathCAD
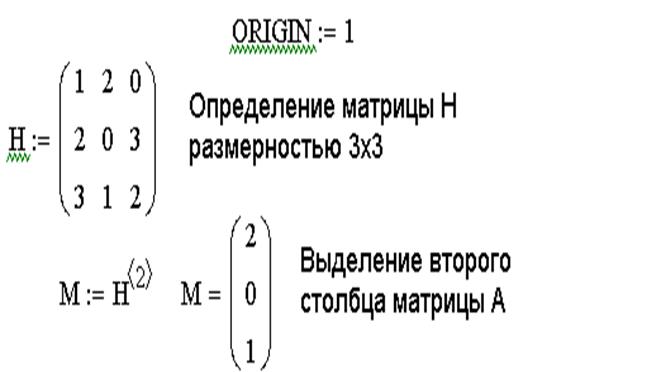
Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.
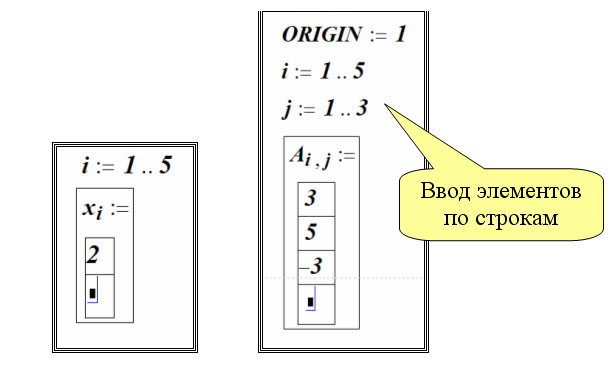
Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.
Поэлементный ввод массива Х
| Вводимые символы | Отображаемые символы |
| X [ 1 Shift+: 5 | X1:=5 |
| X [ 2 Shift+: 8 | X2:= 8 |
| X [ 3 Shift+: 10 | X3:= 10 |
Поэлементный ввод матрицы А
| Вводимые символы | Отображаемые символы |
| A [ 1,1 Shift+: 0.1 | A11 := 0.1 |
| A [ 1,2 Shift+: -2.5 | A12 := -2.5 |
| A [ 2,1 Shift+: -1.0 | A21 := -1.0 |
| A [ 2,2 Shift+: 5.2 | A22 := 5.2 |
Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке 
ПанельMatrix содержит следующие кнопки:









Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки 
1. Ввести с клавиатуры имя матрицы и знак присваивания;
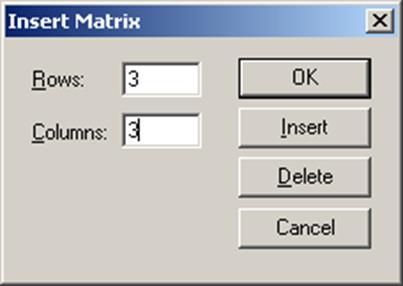
2. Щелчком по кнопке 
3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;
4. Закрыть окно диалога, щелкнув по кнопке OK;
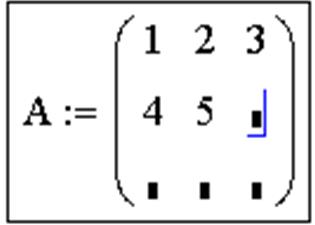
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:
Функции определения матриц и операции с блоками матриц:
matrix(m,n,f) – создает и заполняет матрицу A=<aij> размерности m на n, каждый элемент которой aij равен значению функции f(i,j);
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число строк);
stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l
Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;
Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;
Функции вычисления различных числовых характеристик матриц:
last(v) – вычисление номера последнего элемента вектора v;
length(v) – вычисление количества элементов вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице (векторе) А;
min(A) – вычисление наименьшего элемента в матрице (векторе) А;
mean(A) – вычисление среднего значения матрицы (вектора) А;
tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;
ranc(A) – вычисление ранга матрицы А;
Функции, реализующие численные алгоритмы:
rref(A) – приведение матрицы А к ступенчатому виду;
geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;
lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.
lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;
qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;
cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙L T , где А — квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;
sort(v) – сортировка элементов вектора v в порядке возрастания их значений;
reverse(v) – перестановка элементов вектора v в обратном порядке;
csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;
rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.
ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.
ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.
ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.
ЗАДАЧА 4. Элементы матрицы формируются по формуле 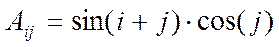
ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:
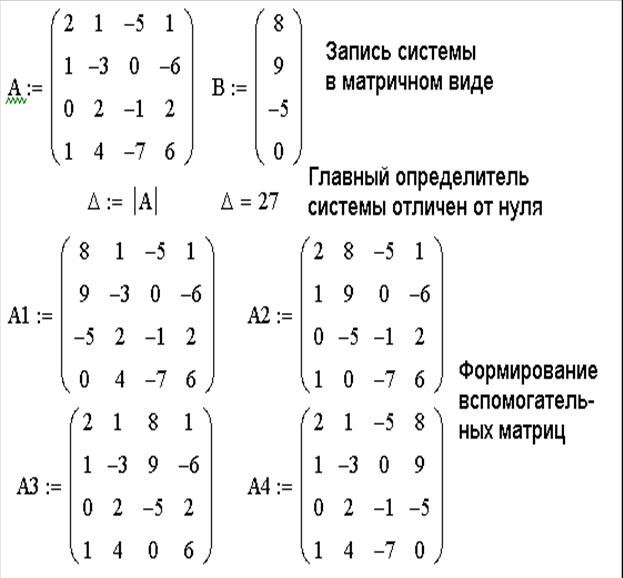
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:
Для решения поставленной задачи необходимо выполнить следующие действия:
1. Сформировать матрицу системы А и вектор правых частей b.
2. Вычислить главный определитель ∆.
3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆i;
4. Вычислить определители ∆i;
5. Найти решение системы по формуле xi=∆i/∆.
ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.
1. Сформировать матрицу коэффициентов и вектор свободных членов системы.
2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.
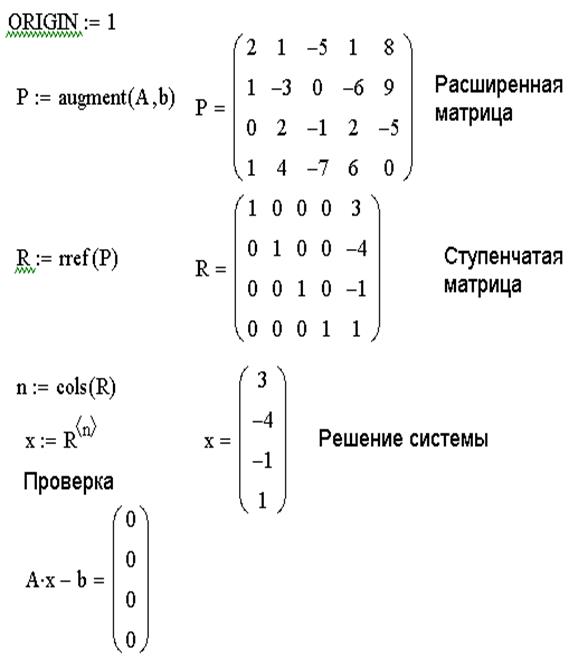
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.
Порядок решения задачи:
1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.
2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);
3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.
4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.
5. Выполнить проверку Ax-B=0.
ЗАДАЧА 9. Решить систему при помощи функции lsolve:
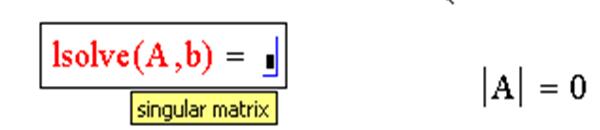
Пример системы, которая не имеет решений:
Пример системы, которая имеет бесконечное множество решений
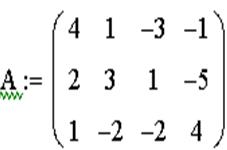
ЗАДАЧА 10. Решить систему при помощи решающего блока.
Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.
Правее и ниже ключевого слова записываются уравнения системы.
Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.
Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.
Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).
Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).
Видео:7. MathCad. Векторы и матрицыСкачать

Последний элемент вектора маткад
Столбец чисел называется вектором, а прямоугольная таблица чисел — матрицей. Общий термин для вектора или матрицы — массив. При работе с матрицами используется панель инструментов “Матрицы”:
Обращение к элементам массива
Обращение к элементу массива осуществляется путем записи имени массива и соответствующих индексных выражений, количество которых определяется размерностью массива.
Для ввода индексных выражений обязательно нажать клавишу [ [ ] – левую квадратную скобку. При этом курсор перемещается вниз, и индексные выражения оказываются смещенными относительно имени массива.
Внимание! После завершение ввода индексных выражений обязательно охватить выделяющим уголком имя и индексные выражения массива.
Внимание! Смещение вниз вызывает также нажатие клавиши 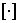
На рисунке показан фрагмент присваивания значений отдельным элементам массивов: векторов 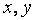
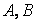
Начальное значение индексных выражений определяется системной переменной 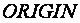
Для перехода к привычной нумерации (с начального значения 1) необходимо изменить значение системной переменной 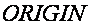
Это можно осуществить двумя способами:
а) задать в документе новое значение с помощью оператора присваивания (область действия нового значения – весь ниже лежащий документ);
б) обратиться к пункту меню Математика команда Опции и в появившемся диалоговом окне изменить значение опции Исходное множество на нужное значение (например, 1).
Верхний индекс матрицы
Верхний индекс – позволяет обратиться к отдельному столбцу массива.
Чтобы вставить верхний индекс, введите имя массива, а затем нажать клавиши
или нажать на кнопку 
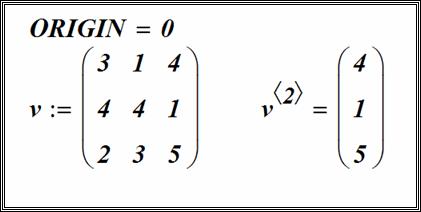
Создание вектора и матрицы
Способ 1. Заполнение шаблона.
· введите имя матрицы и знак присваивания (двоеточие)
· щелкните по значку 
· После нажатия кнопки OK открывается поле для ввода элементов матрицы. Заполните метки — заполнители соответствующими значениями.
Примеры определения векторов и матриц:
Способ 2. Ввод с клавиатуры в цикле
Способ 3. Формирование элементов по заданному выражению.
Сформировать вектор по правилу 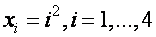
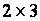
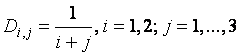
Изменение размера матрицы
Можно изменять размер матрицы, вставляя и удаляя строки и столбцы. Для этого необходимо выполнить следующее:
· Щёлкните на одном из элементов матрицы, чтобы заключить его в выделяющую рамку.
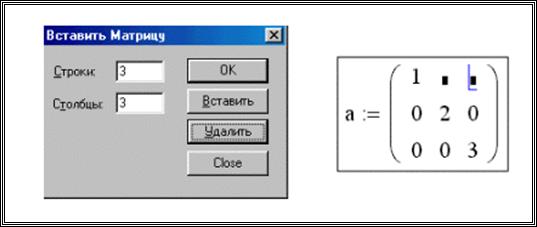
· Щелкните по значку “создать матрицу” в панели “Матрицы. Появляется диалоговое окно.
· Напечатайте число строк и (или) столбцов, которые нужно вставить или удалить. Затем нажмите на “Вставить” или на “Удалить”.
Например, чтобы удалить 1-й столбец, выделите элемент столбца (число 2), вызовите диалоговое окно “создать матрицу”, напечатайте 1 в поле “Столбцов”, 0 в поле “Строк”, и нажмите на “Удалить”.

Рассмотрим различные ситуации удаления или вставки строк или столбцов:
· Если вставляются строки, Mathcad создает строки пустых полей ниже выбранного элемента. Если вставляются столбцы, Mathcad создает столбцы пустых полей справа от выбранного элемента.
· Чтобы вставить строку выше верхней строки или столбец слева от первого столбца, сначала заключите матрицу целиком в выделяющую рамку, щёлкнув внутри и нажав клавишу пробел несколько раз. Затем щелкните по значку “создать матрицу” и продолжите, как обычно.
· Когда удаляются строки или столбцы, Mathcad удаляет строки вниз от этого элемента, а столбцы — направо от этого элемента.
Внимание. При удалении строк или столбцов Mathcad удаляет содержащуюся в них информацию.
💥 Видео
Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

Урок 4. МКЭ в Mathcad. Вектор узловой нагрузкиСкачать

Урок 3. МКЭ в Mathcad. Векторы геометрических характеристикСкачать

Функции для работы с матрицами и векторами в MathCAD 14 (21/34)Скачать
МАТКАД МатрицыСкачать
Векторы и матрицыСкачать
MATLAB 04 Массивы и матрицыСкачать

MathCAD Простейшие действия с матрицамиСкачать
Matlab Tutorial - 27 - Extracting a Subset of Vector ElementsСкачать

Векторная диаграмма токов в программе MathcadСкачать

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать
Find sum of vector elements in MATLABСкачать

Математика это не ИсламСкачать

Матрицы и векторы. Настройки Mathcad при работе с матрицами. Урок 12Скачать

Урок 7. МКЭ в Mathcad. Матрицы инциденций, жесткости и вектор перемещений ДМСкачать