Построение графика y tgx с помощью единичной окружности (5 видео)

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №5. Свойства и график функции y=tgx и y=ctg x

Перечень вопросов, рассматриваемых в теме

Изучение и объяснение свойств функций y=tgx и y=ctgx с помощью графика;
Определение свойств и положения графика тригонометрических функций вида y=|tg(k|x|+b)| y=|ctg(k|x|+b|;
Объяснение зависимости свойств и положения графика функции вида y=|tg(k|x|+b)| и y=|ctg(k|x|+b| от значения коэффициентов k,b.

Глоссарий по теме

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Тангенсоида –график функции у = tgx; плоская кривая, изображающая изменение тангенса в зависимости от изменения его аргумента (угла).

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].–Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

1. ;

Ответ:

Объяснение нового материала

Изучение свойств функции y=tgx начнем с построения графика. Обратимся к единичной окружности:

рис.1 Тригонометрический круг

Переносим основные значения углов на координатную плоскость. По оси абсцисс откладываем угол в радианах, по оси ординат – значения тангенса угла.

рис.2 График y=tgx на промежутке

Как любая тригонометрическая функции, функция тангенса периодическая, делая параллельный перенос получаем:

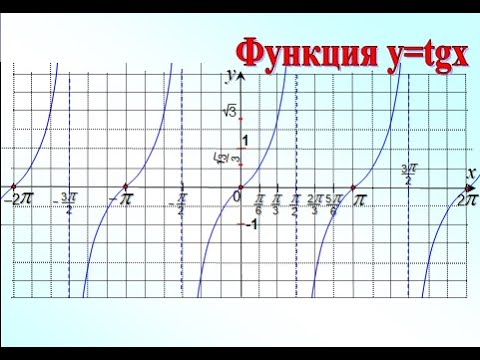
рис.3 График y=tgx

Заметим, что график симметричен относительно начала координат, следовательно функция тангенса нечётная. Используя построенный нами график, выведем основные свойства y=tgx:

1. Область определения функции y = tgx все действительные числа, кроме чисел вида

2. Функция периодическая с периодом , т.к.

3. Функция нечётная, т.к. . График нечётной функции симметричен относительно начала координат;

4. Функция возрастает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

7. Функция принимает:

значение, равное 0, при ;
положительные значения на интервале
отрицательные значения на интервале

Для построения графика можно придерживаться алгоритму рассмотренному при построении графика , однако (формула приведения). Т.е. смещая тангенсоиду на единиц влево и делаем симметрию относительно оси Ох за счёт коэффициента –1, получаем:

рис.3 График y=сtgx

Основные свойства y=сtgx:

1. Область определения функции y = сtgx все действительные числа, кроме чисел вида

2. Функция периодическая с периодом ;

3. Функция нечётная. График нечётной функции симметричен относительно начала координат;

4. Функция убывает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

6. .

Примеры и разборы решения заданий тренировочного модуля:

Найдем все корни уравнения , принадлежащие отрезку .

Построим графики функций и (рис. 6)

Рис. 4 – графики функций и .

Графики пересекаются в трёх точках, абсциссы которых являются корнями уравнения .

Ответ:

Пример 2. Найти все решения неравенства , принадлежащие отрезку .

рис.5 графики функций и

Графики пересекаются в трёх точках, абсциссы которых являются корнями уравнения .

Ответ:

Видео:Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать

Объяснение и обоснование

Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем

Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.

Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все

Значенияx входят в область определения функции y=tgx.

Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т

очек на линии тангенсов принимают

все значения до +, поскольку для любого действительного числа

мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит

внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку

(на самом деле их две). Следовательно, для любого действительного числа

найдется аргумент х, такой, что tan x равен данному действительному числу.

Поэтому область значений функции y= tg x — все действительные числа,

то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.

Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.

Тангенс — периодическая функция с наименьшим положительным периодом

Поэтому при построении графика

этой функции достаточно построить график на любом промежутке длиной π,

а потом полученную линию перенести параллельно вправо и влево вдоль оси

Ox на расстоянияkT = πk, где k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,

при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при

а также, учитывая период, при всех

Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,

Промежутки возрастания и убывания.

Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,

например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии

тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом

промежутке функция tgx возрастает. Учитывая периодичность функции

tgx, делаем вывод, что она возрастает также на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график

функции y = tg x. Учитывая периодичность этой функции (с периодом π),

сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки

линии тангенсов. На рисунке 93 показано построение графика функции

y = tg x на промежутке.

Далее, учитывая периодичность тангенса (с периодом π), повторяем вид

графика на каждом промежутке длиной π (то есть параллельно переносим

график вдоль оси Ох на πk, где k — целое число).

Получаем график, приведенный на рисунке 94, который называется тангенсоидой.

14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК

Объяснение и обоснование

Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,

D (ctg x): x ≠ πk, k ∈ Z.

Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии

котангенсов (рис. 95).

Поскольку точки А и В единичной окружности лежат на прямых ОА

и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.

Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.

Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.

Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.

Там же было обосновано, что котангенс — периодическая функция с наименьшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.

На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D(рис. 95), то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех

Значения функции котангенс отрицательны (то есть абсцисса соответствующей точки линии котангенсов отрицательна) во II и IV четвертях, таким образом, ctgx x₁) абсцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx₂

Видео:Построение графика функции y=tg xСкачать

Функция y=tgx, ее свойства и график

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим функцию у = tg t, ее свойства и график. В начале урока вспомним определение функции как закона соответствия и определение графика функции. Далее дадим определение функции у = tg t на числовой окружности и рассмотрим линию тангенсов — касательную к окружности. Найдем область значений функции и обсудим два важных свойства функции — нечетность и периодичность. Построим график функции тангенс с учетом ее свойств. Рассмотрим все свойства функции у = tg t.

Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Тригонометрия»