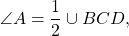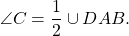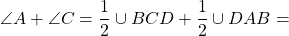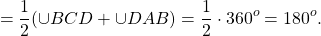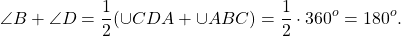Поскольку abcd выпуклый и abd acd получаем что около четырехугольника abcd можно описать окружность (4 видео)

Поскольку abcd выпуклый и abd acd получаем что около четырехугольника abcd можно описать окружность

В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.

Решение . Поскольку ABCD выпуклый и &angle;ABD = &angle;ACD, получаем, что около четырёхугольника ABCD можно описать окружность. А тогда &angle;DAC = &angle;DBC как вписанные углы, опирающиеся на одну дугу CD.

Содержание

Около четырехугольника можно описать окружность
Докажите, что если в выпуклом четырехугольнике ABCD ∠ABD = ∠ACD, то вокруг него можно описать окружность?
В выпуклом четырехугольнике ABCD проведены диагонали?
Докажите что выпуклый четырехугольник ABCD является параллелограммом если BAC = ACD и BCA = DAC?
Докажите, что у четырехугольника, описанного около окружности, суммы длин противолежащих сторон равны?
В выпуклом четырехугольнике ABCD углы ABD и ABC равны?
В выпуклом четырехугольнике ABCD углы ACD = ABD?
ПОМОГИТЕ, ЛЮДИ ДОБРЫЕ?
Дан выпуклый четырехугольник ABCD со сторонами АВ = 9, BC = CD = 11, AD = 15 и диагональю АС = 16?
В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник?
Вокруг выпуклого четырёхугольника ABCD описана окружность?
6. В четырехугольнике ABCD AB = DC и BAC = ACD?
📺 Видео

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Около четырехугольника можно описать окружность

Теорема (свойство вписанного четырёхугольника)

Сумма противолежащих углов вписанного четырёхугольника равна 180°.

Дано: ABCD вписан в окр. (O; R)

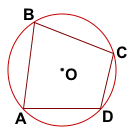
∠A — вписанный угол, опирающийся на дугу BCD.

∠C — вписанный угол, опирающийся на дугу DAB.

Так как вписанный угол равен половине дуги, на которую он опирается, то

Что и требовалось доказать.

Теорема (признак вписанного четырёхугольника)

Около четырёхугольника можно описать окружность, если сумма его противолежащих углов равна 180°.

Дано: ABCD — четырёхугольник,

Доказать: ABCD можно вписать в окружность

Опишем окружность около треугольника ABC и докажем, что точка D лежит на этой окружности.

Доказательство будем вести методом от противного.

Предположим, что точка D не лежит на описанной около треугольника ABD окружности. Тогда D лежит либо внутри этой окружности, либо вне её.

Пусть точка D лежит внутри окружности и луч AD пересекает окружность в точке E.

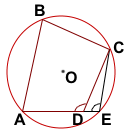
В этом случае четырёхугольник ABCE — вписанный, и сумма его противолежащих углов равна 180°: ∠B+∠E=180°.

По условию, ∠B+∠D=180°. Отсюда следует, что ∠D=∠E.

Но угол D — внешний угол треугольника DCE при вершине D.

Так как внешний угол треугольника равен сумме двух внутренних не смежных с ним углов, то

∠ADC=∠DEC+∠DCE, то есть угол D не может быть равным углу E. Пришли к противоречию. А значит, точка D не может лежать внутри окружности, описанной около треугольника ABC.

Предположим, что точка D лежит вне описанной около треугольника ABC окружности.

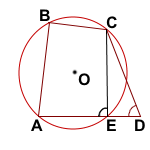
Луч AD пересекает окружность в точке E.

Тогда ABCE — вписанный четырёхугольник и ∠B+∠E=180°.

По условию, ∠B+∠D=180°. Получаем, что ∠D=∠E.

Но угол E — внешний угол треугольника ECD при вершине E. А значит,

∠AEC=∠EDC+∠DCE, то есть углы D и E не могут быть равными. Противоречие получили потому, что предположили, что точка D лежит вне окружности.

Так как точка D не может лежать внутри либо вне описанной около треугольника ABC окружности, то D лежит на этой окружности. Это значит, что около четырёхугольника ABCD можно описать окружность.

Что и требовалось доказать.

На основании свойства и признака вписанного четырёхугольника сформулируем необходимое и достаточное условие вписанного четырёхугольника.

Теорема (Необходимое и достаточное условие вписанного четырёхугольника)

Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма уго противолежащих углов равна 180°.

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Докажите, что если в выпуклом четырехугольнике ABCD ∠ABD = ∠ACD, то вокруг него можно описать окружность?

Геометрия | 5 — 9 классы

Докажите, что если в выпуклом четырехугольнике ABCD ∠ABD = ∠ACD, то вокруг него можно описать окружность.

Около четырехугольника опишем окружность.

Угол ABD = ACD, как вписанные опирающиеся на одну и ту же дугу.

Углы DAC и DBC тоже будут равны т.

К. онивписанные опирающиеся на одну дугу.

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

В выпуклом четырехугольнике ABCD проведены диагонали?

В выпуклом четырехугольнике ABCD проведены диагонали.

Известно, что площади треугольников ABD, ACD, BCD равны.

Докажите, что данный четырехугольник является параллелограммом?

Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

Докажите что выпуклый четырехугольник ABCD является параллелограммом если BAC = ACD и BCA = DAC?

Докажите что выпуклый четырехугольник ABCD является параллелограммом если BAC = ACD и BCA = DAC.

Видео:[ОГЭ] Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120Скачать

Докажите, что у четырехугольника, описанного около окружности, суммы длин противолежащих сторон равны?

Докажите, что у четырехугольника, описанного около окружности, суммы длин противолежащих сторон равны.

Объясните, пожалуйста, какой многоугольник называется выпуклым?

Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

В выпуклом четырехугольнике ABCD углы ABD и ABC равны?

В выпуклом четырехугольнике ABCD углы ABD и ABC равны.

Докажите, что углы DAC и DBC также равны.

Видео:Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

В выпуклом четырехугольнике ABCD углы ACD = ABD?

В выпуклом четырехугольнике ABCD углы ACD = ABD.

Докажите, что углы ACB = ADB.

Видео:Доказать, что точки лежат на одной окружностиСкачать

ПОМОГИТЕ, ЛЮДИ ДОБРЫЕ?

ПОМОГИТЕ, ЛЮДИ ДОБРЫЕ!

Даю 30 баллов в выпуклом четырехугольнике abcd известно что ab = 5, вс корень из 7 cd = ad = 4, ac = 4 корня из 2.

Докажите, что около четырехугольника можно описать окружность.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Дан выпуклый четырехугольник ABCD со сторонами АВ = 9, BC = CD = 11, AD = 15 и диагональю АС = 16?

Дан выпуклый четырехугольник ABCD со сторонами АВ = 9, BC = CD = 11, AD = 15 и диагональю АС = 16.

А) Докажите, что около него можно описать окружность.

Б) Найдите диагональ BD.

Видео:В ромбе ABCD угол АВС равен 148°. Найдите угол ACD. Ответ дайте в градусах.Скачать

В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник?

В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник.

Найдите отношения периметров и площадей этих четырехугольников.

Видео:В трапеции ABCD AB=CD, ∠BDA=35° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Вокруг выпуклого четырёхугольника ABCD описана окружность?

Вокруг выпуклого четырёхугольника ABCD описана окружность.

К — точка пересечения диагоналей данного четырёхугольника.

Угол ВKС = 60 градусов, АВ = 43, DС = 4.

Найти радиус описанной окружности.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

6. В четырехугольнике ABCD AB = DC и BAC = ACD?

6. В четырехугольнике ABCD AB = DC и BAC = ACD.

Докажите, что AD = BC.

Вы находитесь на странице вопроса Докажите, что если в выпуклом четырехугольнике ABCD ∠ABD = ∠ACD, то вокруг него можно описать окружность? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Я так понимаю что С = 90, а A = 60. Сумма углов треугольника равна 180 градусов из этого 180 — (60 + 90) = 30 уголB. Если на против катета лежит угол 30 градусов то катет равен половине гипотенузы 8 * 2 = 16 сторона AC.

Сумма острых углов прямоугольного треугольника равна 90°, отсюда : ∠В = 90 — ∠А = 90 — 60 = 30° Катет, лежащий против угла 30° равен 1 / 2 гипотенузы, отсюда : АВ = 2ВС = 2 * 8 = 16 см Ответ : 16 см.

5 — 9 классы Геометрия 5 + 3 б ПОМОГИТЕ ПОЖАЛУЙСТА ОЧЕНЬ СРОЧНО Дано : А(7 ; — 4), В( — 2 ; — 10), С(0 ; 5). Найти : а) координаты вектора ВС ; б) длину вектора АВ ; в) координаты середины отрезка АС ; г) периметр треугольника АВС ; д) длину мед..

Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольникапараллельна третьей стороне, а ее длина равна половине длины этой стороны.

Средняя линия треугольникапараллельна третьей стороне, а ее длина равна половине длины этой стороны.

3. AB = 17, CE = 12, DE = 6 св — ва хорд AE * BE = CE * DE нам нужно найти AE и BE, поэтому обозначим AE = x, тогда т. К. AB = 17, то BE = (17 — x), получим x * (17 — x) = 12 * 6 17 * x — x² = 72 x² — 17 * x + 72 = 0 D = 289 — 4 * 1 * 72 = 289 — 288..

4. Посмотри на фото.