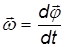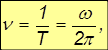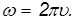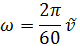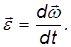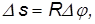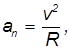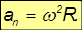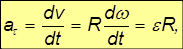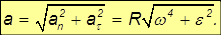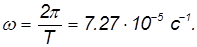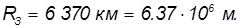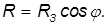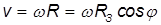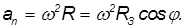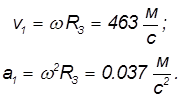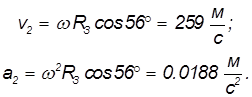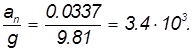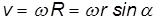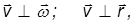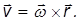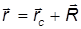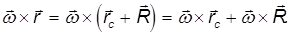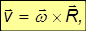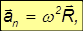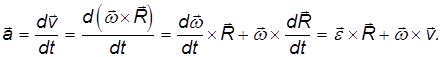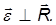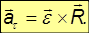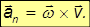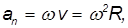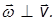Рассмотрим кинематику движения протяженного тела, размерами которого в условиях рассматриваемой задачи пренебречь нельзя. Тело будем считать недеформируемым, другими словами, — абсолютно твердым.
Движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе, называется поступательным.
Под прямой «жестко связанной с телом» понимается такая прямая, расстояние от любой точки которой до любой точки тела остается постоянным при его движении.
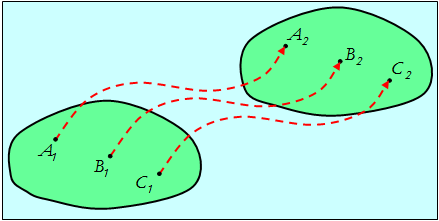
Поступательное движение абсолютно твердого тела можно охарактеризовать движением какой-либо точки этого тела, так как при поступательном движении все точки тела движутся с одними и теми же скоростями и ускорениями, а траектории их движения конгруэнтны. Определив движение какой-нибудь из точек твердого тела, мы вместе с тем определим движение всех остальных его точек. Поэтому при описании поступательного движения не возникает новых проблем по сравнению с кинематикой материальной точки. Пример поступательного движения показан на рис. 2.20.
Рис.2.20. Поступательное движение тела
Пример поступательного движения показан на следующем рисунке:
Рис.2.21. Плоское движение тела
Другой важный частный случай движения твердого тела — это движение, при котором две точки тела остаются неподвижными.
Движение, при котором две точки тела остаются неподвижными, называется вращением вокруг неподвижной оси.
Прямая, соединяющая эти точки, также неподвижна и называется осью вращения.
Рис.2.22. Вращение твердого тела
При таком движении все точки тела движутся по окружностям, расположенным в плоскостях, перпендикулярных оси вращения. Центры окружностей лежат на оси вращения. При этом ось вращения может находиться и вне тела.
Видео 2.4. Поступательное и вращательное движения.
Угловая скорость, угловое ускорение. При вращении тела вокруг какой-либо оси все его точки описывают окружности различного радиуса и, следовательно, имеют различные перемещения, скорости и ускорения. Тем не менее, можно описать вращательное движение всех точек тела одинаковым образом. Для этого используют иные (по сравнению с материальной точкой) кинематические характеристики движения — угол поворота 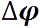
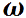
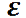
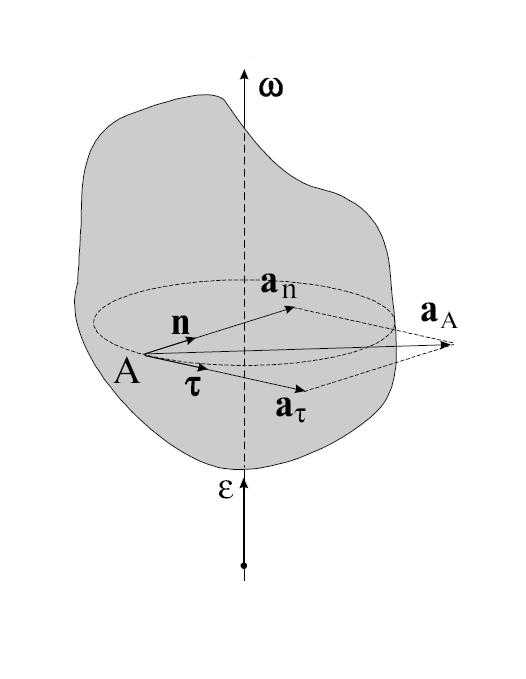
Рис. 2.23. Вектора ускорения точки, движущейся по окружности
Роль перемещения 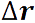
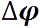
Рис. 2.24. Вращение абсолютно твердого тела вокруг неподвижной оси
Модуль вектора поворота равен величине угла поворота 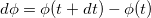
Направлен вектор бесконечно малого поворота по оси вращения в сторону движения правого винта (буравчика), вращаемого в том же направлении, что и тело.
Видео 2.5. Конечные угловые перемещения — не векторы, так как не складываются по правилу параллелограмма. Бесконечно малые угловые перемещения – векторы.
Векторы, направления которых связаны с правилом буравчика, называют аксиальными (от англ. axis — ось) в отличие от полярных. векторов, которыми мы пользовались ранее. Полярными векторами являются, например, радиус-вектор, вектор скорости, вектор ускорения и вектор силы. Аксиальные векторы называют также псевдовекторами, так как они отличаются от истинных (полярных) векторов своим поведением при операции отражения в зеркале (инверсии или, что то же самое, переходе от правой системы координат к левой). Можно показать (это будет сделано позже), что сложение векторов бесконечно малых поворотов происходит так же как и сложение истинных векторов, то есть по правилу параллелограмма (треугольника). Поэтому, если операция отражения в зеркале не рассматривается, то отличие псевдовекторов от истинных векторов никак не проявляет себя и обходиться с ними можно и нужно как с обычными (истинными) векторами.
Отношение вектора бесконечно малого поворота ко времени, за которое этот поворот имел место
называется угловой скоростью вращения.
Основной единицей измерения величины угловой скорости является рад/с. В печатных изданиях, по причинам никакого отношения к физике не имеющим, нередко пишут 1/с или с -1 , что, строго говоря, неверно. Угол — величина безразмерная, но единицы его измерения различны (градусы, румбы, грады …) и их необходимо указывать, хотя бы во избежание недоразумений.
Видео 2.6. Стробоскопический эффект и его использование для дистанционного измерения угловой скорости вращения.
Угловая скорость 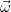
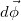
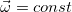
Период вращения — это время, за которое тело совершает один оборот (поворот на угол 2π) вокруг оси вращения.
Слова «достаточного постоянства» означают, очевидно, что за период (время одного оборота) модуль угловой скорости меняется несущественно.
Часто используют также число оборотов в единицу времени
При этом в технических приложениях (прежде всего, всякого рода двигатели) в качестве единицы времени общепринято брать не секунду, а минуту. То есть угловая скорость вращения 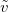

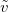
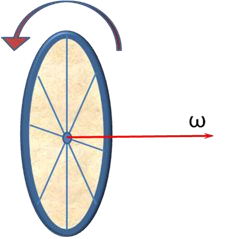
Направление вектора угловой скорости показано на рис. 2.25.
Рис. 2.25. Направление вектора угловой скорости
По аналогии с линейным ускорением вводится угловое ускорение 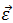
Угловое ускорение 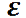
При вращении вокруг неподвижной оси, в более общем случае при вращении вокруг оси, которая остается параллельной самой себе, вектор угловой скорости также направлен параллельно оси вращения. При возрастании величины угловой скорости |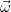
Связь угловых и линейных скоростей и ускорений. Каждая из точек вращающегося тела движется с определенной линейной скоростью 
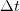
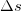
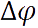
Переходя к пределу 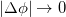
Напомним, здесь R — расстояние от рассматриваемой точки тела до оси вращения.
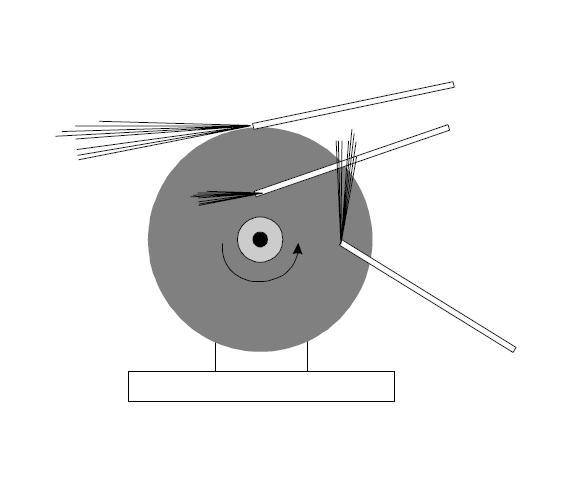
Рис. 2.27. Направление движения искр при заточке инструментов.
Так как нормальное ускорение равно
то с учетом соотношения для угловой и линейной скорости получаем
Нормальное ускорение точек вращающегося твердого тела часто называют центростремительным ускорением.
Дифференцируя по времени выражение для 
где 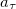
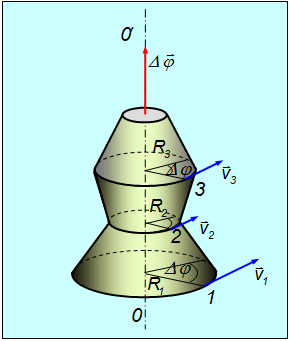
Таким образом, как тангенциальное, так и нормальное ускорения растут линейно с ростом радиуса R — расстояния от оси вращения. Полное ускорение также линейно зависит от R :
Пример. Найдем линейную скорость 
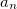
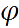
Средний радиус Земли
Расстояние до оси вращения на широте 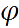
Отсюда находим линейную скорость
и центростремительное ускорение
На экваторе 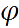
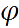
На широте Москвы cos 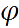
Мы видим, что влияние вращения Земли не столь велико: отношение центростремительного ускорения на экваторе к ускорению свободного падения равно
Тем не менее, как мы увидим в дальнейшем, эффекты вращения Земли вполне наблюдаемы.
Связь между векторами линейной и угловой скорости. Полученные выше соотношения между угловой и линейной скоростью записаны для модулей векторов 

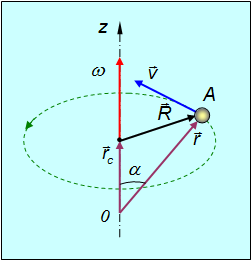
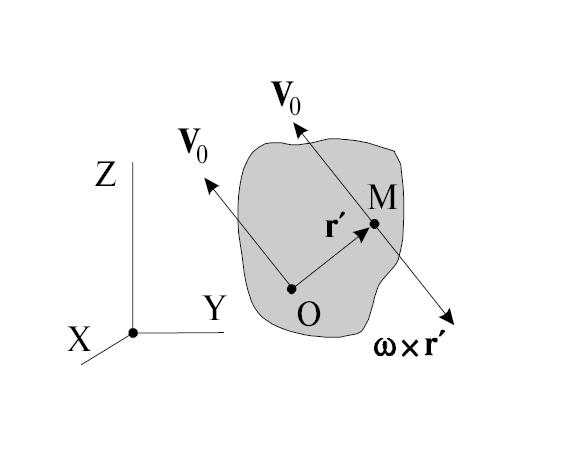
Пусть 0z — ось вращения абсолютно твердого тела (рис. 2.28).
Рис. 2.28. Связь между векторами линейной и угловой скорости
Точка А вращается по окружности радиусом R. R — расстояние от оси вращения до рассматриваемой точки тела. Примем точку 0 за начало координат. Тогда
то по определению векторного произведения, для всех точек тела
Здесь 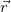
Но, с другой стороны
Первое слагаемое равно нулю, так как векторное произведение коллинеарных векторов равно нулю. Следовательно,
где вектор R перпендикулярен оси вращения и направлен от нее, а его модуль равен радиусу окружности, по которой движется материальная точка и начинается этот вектор в центре этой окружности.
Рис. 2.29. К определению мгновенной оси вращения
Нормальное (центростремительное) ускорение также можно записать в векторной форме:
причем знак «–» показывает, что оно направлено к оси вращения. Дифференцируя соотношение для линейной и угловой скорости по времени, находим для полного ускорения выражение
Первое слагаемое направлено по касательной к траектории точки на вращающемся теле и его модуль равен 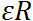
Сравнивая с выражением для тангенциального ускорения, приходим к выводу, что это — вектор тангенциального ускорения
Следовательно, второе слагаемое представляет собой нормальное ускорение этой же точки:
Действительно, оно направлено вдоль радиуса R к оси вращения и его модуль равен
Поэтому данное соотношение для нормального ускорения является другой формой записи ранее полученной формулы.
Видео:Физика | Ликбез по векторамСкачать

Полярные и аксиальные векторы
Пойдем дальше. Вы видели, что в физике имеется масса примеров применимости правила правой и левой руки. В самом деле, когда мы изучали векторный анализ, то узнали о правиле правой руки, которым необходимо пользоваться, чтобы получить правильный момент количества движения и момент силы, магнитное поле и т. п. Например, сила, действующая на заряд в магнитном поле, равна 



Представьте себе, что какой-то озорной чертик, решив подшутить над физиками, пробрался во все лаборатории и всюду заменил слово «правое» на «левое». И в результате, где было написано правило правой руки, мы вынуждены были бы пользоваться правилом левой руки. Ну что ж, физики бы просто не заметили этого, ибо ни к какому изменению в физических законах это бы не привело, разумеется, если физические законы симметричны.
Покажем это на примере. Вы знаете, что существуют два сорта векторов. Имеются обыкновенные, «настоящие» векторы, подобные, например, отрезку расстояния 
Фиг. 52.2. Отрезок в пространстве и его зеркальное отражение.
Но второй сорт векторов, связанных с вращением, имеет совсем другую природу. Представьте себе нечто вращающееся в трехмерном пространстве (фиг. 52.3). Если посмотреть на это в зеркало, то вращение будет происходить так, как показано на рисунке, т. е. как зеркальное изображение первоначального вращения. Условимся теперь представлять зеркальное вращение с помощью того же самого правила. В результате мы получим «вектор», который в отличие от полярного вектора не изменяется при отражении и оказывается перевернутым по отношению к полярному вектору и геометрии всего пространства. Такой вектор мы называем аксиальным.
Фиг. 52.3. Вращающееся колесо и его зеркальное отражение.
Заметьте, что направление «вектора» угловой скорости не изменяется.
Если физический закон симметрии относительно отражения правилен, то уравнения должны быть устроены так, чтобы при изменении знака каждого аксиального вектора и каждого векторного произведения (что соответствует отражению) ничего не произошло. Например, когда мы пишем формулу для момента количества движения 










Давайте посмотрим на примере, как это все получается. Пусть у нас имеются два магнита, похожих на изображенные на фиг. 52.4. Один из магнитов выглядит в точности так, как зеркальное отражение другого, т. е. витки его накручены в другую сторону, и все, что происходит внутри катушки, должно быть в точности обращено в другую сторону; ток течет, как это показано на рисунке. Теперь из законов магнетизма (которые вы хотя еще и не знаете официально, но, по-видимому, помните из школьного курса) получается, что магнитное поле направлено так, как это показано на рисунке. Там, где у первого магнита южный полюс, у другого магнита будет северный, ибо у него ток течет в другую сторону, а магнитное поле перевернуто. Таким образом, выходит, что при переходе от правой системы к левой мы действительно должны заменить северный полюс на южный!
Фиг. 52.4. Электромагнит и его зеркальное отражение.
Но северный и южный полюсы — это просто договоренность, и замена их еще ничего не означает. Давайте посмотрим на само явление. Предположим, что электрон движется от нас через магнитное поле перпендикулярно к плоскости страницы. Тогда, если воспользоваться формулой для силы 
А теперь проделаем тот же опыт с зеркально отраженным магнитом: пошлем электрон в соответствующем направлении. Теперь на него будет действовать обратная сила. Вычислив ее по тем же правилам, мы получим правильный результат: соответствующее движение будет зеркальным отражением предыдущего!
Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Полярный и аксиальный векторы
Двинемся дальше. Мы замечаем, что в физике существует много примеров, где мы имеем «левосторонние» и «правосторонние» правила. Когда мы изучали векторный анализ, то узнали правило правой руки, которое должны применять, чтобы верно определить направление момента количества движения, вращающего момента, магнитного поля и так далее. Например, сила, действующая на заряд в магнитном поле, равна F = qv х В. В данной ситуации, когда мы знаем F, v и В, не достаточно ли этого уравнения для определения правосторонности? На самом деле, если мы вернемся назад и посмотрим, откуда появились эти векторы, то поймем, что «правило правой руки» было простым соглашением; это была хитрость. Первоначальные величины, вроде моментов количества движения и угловых скоростей, вовсе не являлись настоящими векторами! Все они как-то связаны с некоторой плоскостью, и только потому, что наше пространство имеет три измерения, мы смогли связать эти величины с направлением, перпендикулярным к этой плоскости. Из двух возможных направлений мы выбрали «правостороннее».
Представьте, что если бы некий демон проник во все физические лаборатории и поменял слово «право» на «лево» во всех книгах, где указаны «правила правой руки», и вместо них мы все использовали «правила левой руки», то физики бы просто не заметили этого, ибо не было бы никакой разницы с точки зрения физических законов, если законы физики симметричны.
Давайте дадим иллюстрацию. Существуют два вида векторов. Есть обыкновенные, «настоящие» векторы, например шаг Лг в пространстве. Если в нашем аппарате имеется некая часть «здесь» и что-то еще «там», то в зеркально отраженном аппарате будет присутствовать отражение части и отражение того же самого «чего-то», а если мы проведем вектор от «сюда» до «туда», то один вектор будет зеркальным отражением другого (рис. 2.2). Вектор изменил свое направление, так же как все пространство повернулось в другую сторону. Такой вектор мы называем полярным вектором.
Рис. 2.2. Шаг в пространстве и его зеркальное отражение
Но другой тип вектора, связанный с вращением, имеет иную природу. Например, пусть в трехмерном пространстве что-нибудь вращается, как показано на рис. 2.3. Если мы посмотрим на это в зеркале, оно будет вращаться, как указано, а именно, как зеркальное отражение первоначального вращения. Условимся представлять отраженное вращение по тому же правилу. В результате мы получим «вектор», который не меняется как полярный вектор, но перевернут относительно полярных векторов и геометрии пространства; такой вектор называется аксиальным вектором,.
Если закон о симметрии отражения справедлив в физике, тогда уравнения должны быть устроены таким образом, что, если мы в соответствии с отражением поменяем знак каждого аксиального вектора и каждого векторного произведения, ничего не произойдет. Например, если мы напишем выражение для углового момента L = г х р, это выражение останется верным, потому что при переходе к левой системе координат мы изменили знак L, хотя и р и г не изменились. Кроме того изменился знак векторного произведения, поскольку мы должны перейти от правила правой руки к правилу левой руки. Другой пример. Мы знаем, что сила, действующая на заряд в магнитном поле, равна F = q х В, но если мы перейдем от правой системы координат к левой, то, поскольку F и v — полярные векторы, изменение знака векторного произведения должно компенсироваться изменением знака В, откуда следует, что В должен быть аксиальным вектором. Другими словами, при таком отражении В должно перейти в — В. Если мы меняем систему координат
Рис. 2.3. Вращающееся колесо и его зеркальное отражение. Заметьте, что «вектор» угловой скорости не изменил направления с правой на левую, то должны также поменять полюса магнита с северного на южный.
Давайте посмотрим на примере, как это получается. Предположим, у нас есть два магнита, как на рис. 2.4. На одном из магнитов намотана проволочная спираль, и ток по ней идет в определенном направлении. Второй магнит похож на отражение первого в зеркале — проволока намотана в другую сторону, и все, что происходит внутри катушки — повернуто наоборот, и ток течет так, как показано на рисунке. Из законов магнетизма (которые мы пока официально не знаем, но которые почти наверняка проходили в школе) следует, что магнитное поле направлено так, как показано на рис. 2.4. В одном случае полюс является южным магнитным полюсом, а в другом — северным, так как у него ток направлен в другую сторону, а магнитное поле перевернуто. Отсюда видно, что, когда мы переходим с правой системы на левую, мы на самом деле должны поменять север на юг!
Не смущайтесь переменой севера на юг — это просто условности. Давайте поговорим о самом явлении. Предположим теперь, что электрон движется от нас в магнитном поле и направляется в сторону данной страницы. Тогда, если мы применим формулу для силы v х В (помните, что заряд отрицательный), то получим, что он отклонится в указанном направлении в соответствии с этим физическим законом. Так что явление заключается в том, что если в катушке течет ток в определенном направлении, то электрон отклонится определенным образом — это физика, и неважно как мы все называли.
Теперь проделаем такой же эксперимент с участием зеркала: мы посылаем электрон в соответствующем направлении, и если теперь вычислить силу по тому же правилу, то сила поменяет направление, и это верный результат, потому что соответствующее движение является зеркальным отражением!
Рис. 2.4. Электромагнит и его зеркальное отражение
🌟 Видео
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Скалярное произведение векторов. 9 класс.Скачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Единичный векторСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Лекция 18. Скалярное произведение векторов и его свойства.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Урок 8. Векторные величины. Действия над векторами.Скачать

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

ГЕОМЕТРИЯ 11 класс: Компланарные векторыСкачать