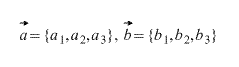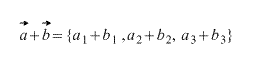Почему сумма двух или нескольких векторов называется геометрической техническая механика

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор

В механике существуют два типа величин:

• скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

• правило параллелограмма
• правило треугольника
• тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

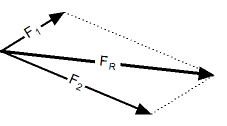Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

	Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

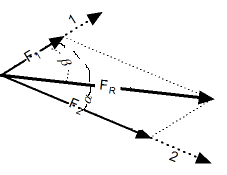Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F1 2 + F2 2 -2 F1 F2 cos(180 о -α) ] 1/2 (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180 o -α) / FR ] (2) где α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

Тема1.2. Плоская система сходящихся сил

§1. Геометрический способ сложения сил

Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, для многих систем сил, как мы увидим в дальнейшем, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.

Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сло­жением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил

(рис. 1, a), откладываем от произвольной точки О (рис. 1, б) век­тор Oa, изображающий в выбранном масштабе cилу F₁, от точки a откладываем вектор

, изображающий силу F₂, от точки b откла­дываем вектор bc, изображающий силу F₃ и т. д.; от конца m пред­последнего вектора откладываем вектор mn, изображающий силу F_n. Соединяя начало первого вектора с концом последнего, получаем вектор

, изображающий геометрическую сумму или главный вектор слагаемых сил:

От порядка, в котором будут откладываться векторы сил, модуль и направление не зависят. Легко видеть, что проделанное по­строение представляет собою результат последовательного приме­нения правила силового тре­угольника.

Рис.1. Система сил

Фигура, построенная на рис. 1,б, называется силовым (в общем случае векторным) многоугольником. Таким обра­зом, геометрическая сумма или главный вектор несколь­ких сил изображается замы­кающей стороной силового многоугольника, построенно­го из этих сил (правило сило­вого многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора

— в сторону противоположную.

Сходящимися называются силы, линии дей­ствия которых пересекаются в одной точке, называемой центром системы (см. рис. 1, а).

По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис. 1, а в точке А).

Последовательно применяя аксиому параллелограмма сил, прихо­дим к выводу, что система сходящихся сил имеет равнодей­ствующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы

сходятся в точке A (рис. 1, а), то сила, равная главному вектору , найденному построением силового мно­гоугольника, и приложенная в точке А, будет равнодействующей этой системы сил.

Примечания.

1. Результат графического определения равнодействующей не изменится, если силы суммировать в другой последовательности, хотя при этом мы получим другой силовой многоугольник — отличный от первого.

2. Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.

3. Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.

§2.Равновесие системы сходящихся сил

Из законов меха­ники следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инер­ции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.

Отсюда получаем два важных вывода:

1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции».

2) Уравно­вешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравнове­шенных сил.

Для равновесия приложенной к твердому телу системы сходя­щихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовле­творять сами силы, можно выразить в геометрической или аналити­ческой форме.

1. Геометрическое условие равновесия. Так как равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то

ПРОЕКЦИИ ГЕОМЕТРИЧЕСКОЙ СУММЫ ВЕКТОРОВ НА ОСЬ

Теорема. Проекция геометрической суммы векторов на какую-либо ось равна алгебраической сумме проекций составляющих векторов на ту же ось.

Пусть дано несколько векторов, например F_v F_v F₃ и F₄ (рис. 1.2.6) (для упрощения чертежа взяты векторы, расположенные в одной плоскости, но теорема остается верной и в общем случае).

По правилу сложения векторов геометрическая сумма, т.е. равнодействующий вектор ЛЕ = F _н, представляет собой замыкающую сторону векторного многоугольника ABCDE, сторонами которого служат составляющие векторы.

Проецируя векторы на ось х, получим F_]x = ab, Е_ъ = Ьс,

Из чертежа видно, что ae = ab + be — cd + de, т.е. что и требовалось доказать.

Данная теорема справедлива для любых векторов и при любом их числе.

АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ РАВНОДЕЙСТВУЮЩЕЙ ПЛОСКОСТИ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ

Мы уже знаем, что равнодействующая системы сходящихся сил равна их геометрической сумме. Кроме того, нам известно, что проекция геометрической суммы векторов на какую-либо ось равна алгебраической сумме проекций составляющих векторов на эту же ось.

Так как это положение справедливо для любых векторов, следовательно, проекция равнодействующей системы сходящихся сил на какую-либо ось равна алгебраической сумме проекций составляющих сил на ту же ось.

Обозначая проекции равнодействующей ^_равн на координатные оси хну через F_pamx и F_pamy, а проекции составляющих сил на те же оси, как это часто принято, F_x и F_y, получим

Если известны проекции какой-либо силы на две взаимно перпендикулярные оси, в плоскости которых лежит вектор данной силы, то для определения ее модуля и направления можно воспользоваться формулами (1.2.2), (1.2.3). Модуль равнодействующей плоской системы сходящихся сил определяется формулой

УСЛОВИЯ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ

Любая система сходящихся сил может быть заменена равнодействующей. Ясно, что если такая система сходящихся сил находится в равновесии, т.е. эквивалентна нулю, то равнодействующая должна равняться нулю (F_paBH = 0). Это равенство является необходимым и достаточным условием равновесия системы сходящихся сил.

В зависимости от способа определения равнодействующей условие равновесия плоской системы сходящихся сил может быть выражено в двух формах: геометрической и аналитической.

Условие равновесия в геометрической форме.

Геометрически равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника. Если равнодействующая равна нулю, то нужно, чтобы равнялась нулю и замыкающая сторона, следовательно, силовой многоугольник замыкается сам на себе. Отсюда получается следующее условие: для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный для этой системы сил, был замкнутым.

На рис. 1.2.7 построен замкнутый силовой многоугольник для находящейся в равновесии плоской системы сходящихся сил F_v F₂, F₃ и F₄. Заметим, что в замкнутом силовом многоугольнике конец вектора последней силы совпадает с началом вектора первой, а стрелки векторов всех сил направлены в одну и ту же сторону.

Условие равновесия в аналитической форме.

Аналитический модуль равнодействующей определяется по формуле (1.2.4). Но если ^вн = 0, то равно нулю и подкоренное выражение. Так как стоящие под корнем слагаемые как квадраты некоторых (безразлично, положительных или отрицательных) чисел всегда положительны, то Т’_равн может равняться нулю только в том случае, если каждое из этих слагаемых равно нулю в отдельности:

Эти уравнения, выражающие собой в аналитической форме необходимые и достаточные условия равновесия сил, называются уравнениями равновесия.

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы порознь равнялись нулю суммы проекций всех сил на каждую из двух любых взаимно перпендикулярных осей, лежащих в плоскости действия сил.

🔥 Видео