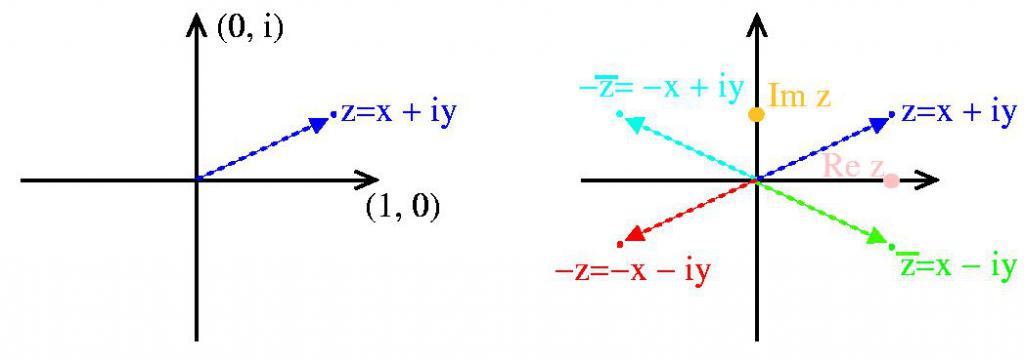Алгебраическая форма записи комплексных чисел Алгебраическая форма записи комплексных чисел |
 Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
 Комплексно сопряженные числа Комплексно сопряженные числа |
 Модуль комплексного числа Модуль комплексного числа |
 Деление комплексных чисел, записанных в алгебраической форме Деление комплексных чисел, записанных в алгебраической форме |
 Изображение комплексных чисел радиус-векторами на координатной плоскости Изображение комплексных чисел радиус-векторами на координатной плоскости |
 Аргумент комплексного числа Аргумент комплексного числа |
 Тригонометрическая форма записи комплексного числа Тригонометрическая форма записи комплексного числа |
 Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера. Экспоненциальная форма записи комплексного числа |
 Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
 Извлечение корня натуральной степени из комплексного числа Извлечение корня натуральной степени из комплексного числа |
- Алгебраическая форма записи комплексных чисел
- Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
- Комплексно сопряженные числа
- Модуль комплексного числа
- Деление комплексных чисел, записанных в алгебраической форме
- Изображение комплексных чисел радиус-векторами координатной плоскости
- Аргумент комплексного числа
- Формула Эйлера. Экспоненциальная форма записи комплексного числа
- Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
- Извлечение корня натуральной степени из комплексного числа
- Комплексные числа: определение и основные понятия
- Историческая справка
- Основные понятия
- Комплексная плоскость
- Тригонометрическая запись
- Модуль и фаза
- Формула Эйлера
- Определение операций
- Извлекаем корень
- Поле и сопряжение
- Примеры
- Зачем нужны комплексные числа
- №15 Основные сведения о комплексных числах.
Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0) .
Комплексные числа, заданные парами (0, y) , называют чисто мнимыми числами .
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи .
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y) , записывается в виде
| z = x + i y . | (1) |
где использован символ i , называемый мнимой единицей .
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z .
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z .
Комплексные числа, у которых Im z = 0 , являются вещественными числами .
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами .
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Видео:Александр Чирцов про комплексные числа и вектораСкачать

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
| i 2 = – 1 . | (2) |
По этой причине
Видео:Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Комплексно сопряженные числа
Два комплексных числа z = x + iy и 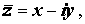
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения , обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
 |  |
 |  |
 |  |
 |  |
 |  |
Видео:Математика это не ИсламСкачать

Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
 |  |
 |  |
 |  |
 |  |
Замечание . Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Видео:Тригонометрическая форма комплексного числаСкачать

Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Видео:✓ Комплексные числа. Введение | Ботай со мной #039 | Борис ТрушинСкачать

Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью , и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью , а ось ординат Oy – мнимой осью .
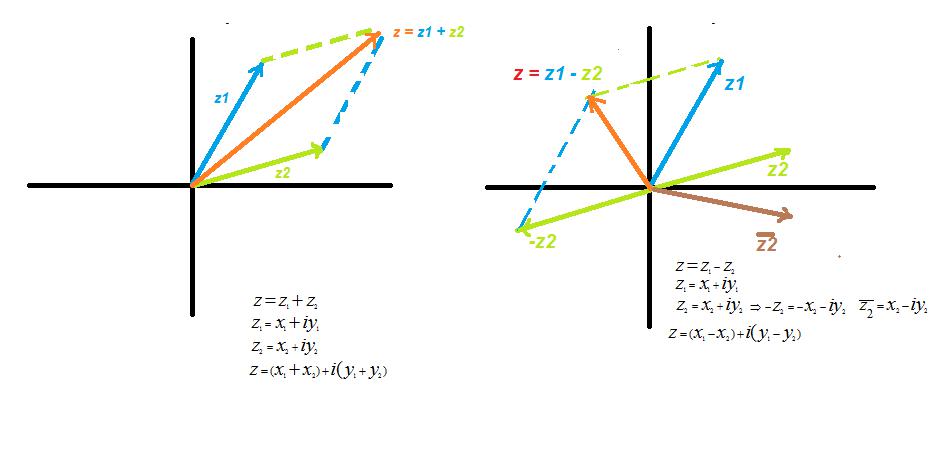
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Видео:1.2 Комплексные числа и их представление векторами на комплексной плоскостиСкачать

Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z .
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z .
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента , обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ , то мы можем найти вещественную и мнимую части по формулам
 | (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y , то модуль этого числа, конечно же, определяется по формуле
 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | 0 | φ = 2kπ |  | |
| Первый квадрант |  |  |  | |
| Положительная мнимая полуось |  |  |  | |
| Второй квадрант |  |  |  | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры |  |
| Расположение числа z | Первый квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Положительная мнимая полуось |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Второй квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Отрицательная вещественная полуось | ||||||||||
| Знаки x и y | Третий квадрант | ||||||||||
| Знаки x и y | Отрицательная мнимая полуось | ||||||||||
| Знаки x и y | Четвёртый квадрант | ||||||||||
| Знаки x и y | |||||||||||
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа .
Видео:2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать

Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r e iφ , | (7) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа .
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
или, что то же самое, числа e iφ , при любом значении φ равен 1.
Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Видео:Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Извлечение корня натуральной степени из комплексного числа
Пусть 
Корнем n — ой степени из числа z0 , где 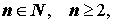
| z n = z0 . | (8) |
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
 | (10) |
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , . , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса 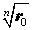
Замечание . В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
Пример 1 . Найти все корни уравнения
то по формуле (10) получаем:
Пример 2 . Решить уравнение
Решение . Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
Видео:Комплексные числа — Алексей Савватеев / ПостНаукаСкачать

Комплексные числа: определение и основные понятия



При изучении свойств квадратного уравнения ставилось ограничение – для дискриминанта меньше нуля решения не существует. Сразу оговаривалось, что речь идет о множестве вещественных чисел. Пытливый ум математика заинтересуется – какой секрет содержится в оговорке о вещественных значениях?
Со временем математики ввели понятие комплексных чисел, где за единицу принимается условное значение корня второй степени из минус единицы.
Видео:Комплексные числа: коротко и понятно – Алексей Савватеев | Лекции по математике | НаучпопСкачать

Историческая справка
Математическая теория развивается последовательно, от простого к сложному. Разберемся, как возникло понятие, получившее название «комплексное число», и зачем оно нужно.
С незапамятных времен основу математики составлял обычный счет. Исследователям было известно только натуральное множество значений. Сложение и вычитание при этом производилось просто. По мере усложнения хозяйственных отношений вместо сложения одинаковых значений начали применять умножение. Появилась обратная операция к умножению – деление.
Понятие натурального числа ограничивало использование арифметических операций. На множестве целых значений невозможно решать все задачи деления. Работа с дробями привела сначала к понятию рациональных значений, а потом и к иррациональным значениям. Если для рационального можно указать точное расположение точки на линии, то для иррациональных такую точку указать невозможно. Можно только приблизительно указать интервал нахождения. Объединение рациональных и иррациональных числе образовали вещественное множество, которое можно представить как некоторую линию с заданным масштабом. Каждый шаг по линии — это натуральное число, а между ними располагаются рациональные и иррациональные значения.
Началась эпоха теоретической математики. Развитие астрономии, механики, физики требовало решения все более сложных уравнений. В общем виде были найдены корни квадратного уравнения. При решении более сложного кубического многочлена ученые столкнулись с противоречием. Понятие кубического корня из отрицательного имеет смысл, а для квадратного получается неопределенность. При этом квадратное уравнение — только частный случай кубического.
В 1545 году итальянец Дж. Кардано предложил ввести понятие мнимого числа.
Таким числом стал корень второй степени из минус единицы. Окончательно термин комплексного числа сформировался только через триста лет, в работах известного математика Гаусса. Он предложил формально распространить на мнимое число все законы алгебры. Вещественная прямая расширилась до плоскости. Мир стал больше.
Видео:Высшая математика. Комплексные числаСкачать

Основные понятия
Вспомним ряд функций, которые имеют ограничения на вещественном множестве:
- y = arcsin(x), определена в интервале значений между отрицательной и положительной единицей.
- y = ln(x), десятичный логарифм имеет смысл при положительных аргументах.
- квадратный корень y = √x, рассчитывается только для x ≥ 0.
Обозначением i = √(-1), введем такое понятие, как мнимое число, это позволит снять все ограничения с области определения вышеприведенных функций. Выражения типа y = arcsin(2), y = ln(-4), y = √(-5) приобретают смысл в некотором пространстве комплексных чисел.
Алгебраическую форму можно записать в виде выражения z = x + i×y на множестве вещественных значений x и y, а i 2 = -1.
Новое понятие снимает все ограничения на использование любой алгебраической функции и своим видом напоминает график прямой в координатах вещественных и мнимых значений.
Видео:10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать

Комплексная плоскость
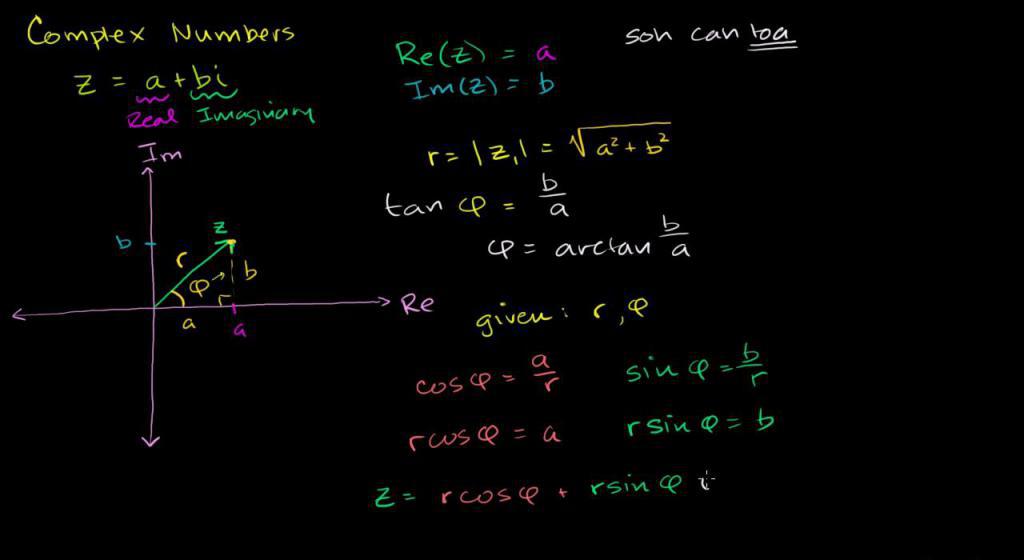
Геометрическая форма комплексных чисел наглядно позволяет представить многие их свойства. По оси Re(z) отмечаем вещественные значения x, по Im(z) — мнимые величины y, тогда точка z на плоскости будет отображать требуемое комплексное значение.
- Re(z) — реальная ось.
- Im(z) – означает мнимую ось.
- z — условная точка комплексного числа.
- Численное значение длины вектора от нулевой точки до z, называется модулем.
- Реальная и мнимая оси разбивают плоскость на четверти. При положительном значении координат — I четверть. При аргументе реальной оси меньше 0, а мнимой больше 0 — II четверть. Когда координаты отрицательные — III четверть. Последняя, IV четверть содержит множество положительных реальных значений и отрицательных мнимых величин.
Таким образом на плоскости со значениями координат x и y всегда можно наглядно изобразить точку комплексного числа. Символ i вводится для отделения реальной части от мнимой.
- При нулевом значении мнимого аргумента получаем просто число (z = x), которое располагается на реальной оси и принадлежит вещественному множеству.
- Особый случай, когда значение реального аргумента становится нулевым, выражение z = i×y соответствует расположению точки на мнимой оси.
- Общий вид z = x + i×y будет при ненулевых значениях аргументов. Означает расположение точки, характеризующей комплексное число, в одной из четвертей.
Видео:Комплексные числа: начало. Высшая математика или школа?Скачать

Тригонометрическая запись
Вспомним полярную систему координат и определение тригонометрических функций sin и cos. Очевидно, что с помощью этих функций можно описать расположение любой точки на плоскости. Для этого достаточно знать длину полярного луча и угол наклона к вещественной оси.
Определение. Запись вида ∣z ∣, умноженное на сумму тригонометрических функций cos(ϴ) и мнимой части i ×sin(ϴ), называется тригонометрическим комплексным числом. Здесь применяется обозначение угол наклона к вещественной оси
ϴ = arg(z), а r = ∣z∣, длина луча.
Из определения и свойств тригонометрических функций, следует очень важная формула Муавра:
z n = r n × (cos(n × ϴ) + i × sin(n × ϴ)).
Используя эту формулу, удобно решать многие системы уравнений, содержащие тригонометрические функции. Особенно когда возникает задача возведения в степень.
Видео:Собственные значения и собственные векторыСкачать

Модуль и фаза
Для завершения описания комплексного множества предложим два важных определения.
Зная теорему Пифагора, легко вычислить длину луча в полярной системе координат.
r = ∣z∣ = √(x 2 + y 2 ), такая запись на комплексном пространстве носит название «модуль» и характеризует расстояние от 0 до точки на плоскости.
Угол наклона комплексного луча к вещественной прямой ϴ принято называть фазой.
Из определения видно, что реальная и мнимая части описываются с помощью циклических функций. А именно:
Обратно, фаза имеет связь с алгебраическими значениями через формулу:
ϴ = arctan(x / y) + µ, поправка µ вводится для учета периодичности геометрических функций.
Видео:Комплексные числа и их представление векторами на комплексной плоскостиСкачать

Формула Эйлера
Математики часто употребляют показательную форму. Числа комплексной плоскости записывают в виде выражения
z = r × e i × ϴ , которая вытекает из формулы Эйлера.
Такая запись получила широкое распространение для практического вычисления физических величин. Форма представления в виде показательных комплексных чисел особенно удобна для инженерных расчетов, где возникает необходимость рассчитать цепи с синусоидальными токами и необходимо знать значение интегралов функций с заданным периодом. Сами расчеты служат инструментом при конструировании различных машин и механизмов.
Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Определение операций
Как уже отмечалось, на комплексные числа распространяются все алгебраические законы работы с основными математическими функциями.
При сложении комплексных значений их реальная и мнимая части также складываются.
z = z1 + z2, где z1 и z2 — комплексные числа общего вида. Преобразуя выражение, после раскрытия скобок и упрощения записи, получим реальный аргумент х=(x1 + x2), мнимый аргумент y = (y1 + y2).
На графике это выглядит как сложение двух векторов, по известному правилу параллелограмма.
Рассматривается как частный случай сложения, когда одно число положительное, другое отрицательное, то есть находящееся в зеркальной четверти. Алгебраическая запись выглядит как разность реальных и мнимых частей.
z = z1 — z2, или, учитывая значения аргументов, аналогично операции сложения, получаем для реальных значений х = (x1 — x2) и мнимых y = (y1 — y2).
Умножение на комплексной плоскости
Используя правила работы с многочленами, выведем формулу для решения комплексных чисел.
Следуя общим алгебраическим правилам z=z1×z2, расписываем каждый аргумент и приводим подобные. Реальную и мнимую части можно записать так:
Красивее смотрится, если будем использовать показательные комплексные числа.
Выражение выглядит так: z = z1 × z2 = r1 × e i ϴ 1 × r2 × e i ϴ 2 = r1 × r2 × e i( ϴ 1+ ϴ 2) .
Далее просто, модули перемножаются, а фазы складываются.
При рассмотрении операции деления, как обратной к операции умножения, в показательной форме записи получаем простое выражение. Деление значения z1 на z2 есть результат деления их модулей и разности фаз. Формально, при использовании показательной формы комплексных чисел это выглядит так:
В виде алгебраической записи операция деления чисел комплексной плоскости записывается немного сложнее:
Расписывая аргументы и проводя преобразования многочленов, легко получить значения х = x1 × x2 + y1 × y2, соответственно y = x2 × y1 — x1 × y2, правда, в рамках описываемого пространства это выражение имеет смысл, если z2 ≠ 0.
Видео:Найти модуль и аргумент комплексного числа #maths #complexnumbers #complexanalysis #тфкп #calculusСкачать

Извлекаем корень
Все вышеописанное можно применять при определении более сложных алгебраических функций – возведение в любую степень и обратную к ней — извлечение корня.
Пользуясь общим понятием возведения в степень n, получаем определение:
z n = (r × e i ϴ ) n .
Используя общие свойства, перепишем в виде:
z n = r n × e i ϴ n .
Получили простую формулу возведения в степень комплексного числа.
Из определения степени получаем очень важное следствие. Четная степень мнимой единицы всегда равна 1. Любая нечетная степень мнимой единицы всегда равно -1.
Теперь изучим обратную функцию – извлечение корня.
Для простоты записи примем n = 2. Квадратным корнем w комплексного значения z на комплексной плоскости C принято считать выражение z = ±, справедливое для любого вещественного аргумента большего или равного нулю. При w ≤ 0 решения не существует.
Посмотрим на самое простое квадратное уравнение z 2 = 1. Используя формулы комплексных чисел, перепишем r 2 × e i 2ϴ = r 2 × e i 2ϴ = e i 0 . Из записи видно, что r 2 = 1 и ϴ = 0, следовательно, имеем единственное решение, равное 1. Но это противоречит понятию, что z = -1, тоже соответствует определению квадратного корня.
Разберемся, что мы не учитываем. Если вспомним тригонометрическую запись, то восстановим утверждение – при периодическом изменении фазы ϴ комплексное число не меняется. Обозначим символом p значение периода, тогда справедлива запись r 2 × e i 2ϴ = e i (0+ p ) , откуда 2ϴ = 0 + p, или ϴ = p / 2. Следовательно, справедливо e i 0 = 1 и e i p /2 = -1. Получили второе решение, что соответствует общему пониманию квадратного корня.
Итак, чтобы найти произвольный корень из комплексного числа, будем действовать по процедуре.
- Запишем показательную форму w= ∣w∣ × e i ( arg ( w ) + pk ) , k — произвольное целое число.
- Искомое число тоже представим по форме Эйлера z = r × e i ϴ .
- Воспользуемся общим определением функции извлечения корня r n *e i n ϴ = ∣w∣ × e i ( arg ( w ) + pk ) .
- Из общих свойств равенства модулей и аргументов, запишем r n = ∣w∣ и nϴ = arg (w) + p×k.
- Итоговая запись корня из комплексного числа описывается формулой z = √∣w∣ × e i ( arg ( w ) + pk ) / n .
- Замечание. Значение ∣w∣, по определению, является положительным вещественным числом, значит, корень любой степени имеет смысл.
Поле и сопряжение
В завершение дадим два важных определения, которые оказывают мало значения для решения прикладных задач с комплексными числами, но существенны при дальнейшем развитии математической теории.
Говорят, что выражения сложения и умножения образуют поле, если удовлетворяют аксиомам для любых элементов комплексной плоскости z:
- От перемены мест комплексных слагаемых комплексная сумма не меняется.
- Верно утверждение — в сложном выражении любую сумму двух чисел можно заменить на их значение.
- Существует нейтральное значение 0, для которого верно z + 0 = 0 + z = z.
- Для любого z существует противоположность – z, сложение с которым дает ноль.
- При перемене мест комплексных множителей комплексное произведение не меняется.
- Умножение двух любых чисел можно заменить на их значение.
- Существует нейтральное значение 1, умножение на которое не меняет комплексное число.
- Для каждого z ≠ 0, есть обратное значение z -1 , умножение на которое дает в результате 1.
- Умножение суммы двух чисел на третье равносильно операции умножение каждого их них на это число и сложение результатов.
- 0 ≠ 1.
Числа z1 = x + i×y и z2 = x — i×y называются сопряженными.
Теорема. Для сопряжения верно утверждение:
- Сопряжение суммы равно сумме сопряженных элементов.
- Сопряжение произведения равно произведению сопряжений.
- Сопряжение сопряжения равно самому числу.
В общей алгебре такие свойства принято называть автоморфизмом поля.
Примеры
Следуя приведенным правилам и формулам комплексных чисел, легко можно ими оперировать.
Рассмотрим простейшие примеры.
Задача 1. Используя равенство 3y +5 x i= 15 — 7i, определить x и y.
Решение. Вспомним определение комплексных равенств, тогда 3y = 15, 5x = -7. Следовательно, x = -7 / 5, y = 5.
Задача 2. Вычислить значения 2 + i 28 и 1 + i 135 .
Решение. Очевидно, 28 — четное число, из следствия определения комплексного числа в степени имеем i 28 = 1, значит, выражение 2 + i 28 = 3. Второе значение, i 135 = -1, тогда 1 + i 135 = 0.
Задача 3. Вычислить произведение значений 2 + 5i и 4 + 3i.
Решение. Из общих свойств умножения комплексных чисел получаем (2 + 5i)Х( 4 + 3i) = 8 — 15 + i(6 + 20). Новое значение будет -7 + 26i.
Задача 4. Вычислить корни уравнения z 3 = -i.
Решение. Вариантов, как найти комплексное число, может быть несколько. Рассмотрим один из возможных. По определению, ∣ — i∣ = 1, фаза для -i равна -р / 4. Исходное уравнение можем переписать в виде r 3 *e i 3ϴ = e — p/4+ pk , откуда z = e — p / 12 + pk/3 , для любого целого k.
Множество решений имеет вид (e — ip/12 , e ip /4 , e i 2 p/3 ).
Зачем нужны комплексные числа
История знает множество примеров, когда ученые, работая над теорией, даже не задумываются о практическом применении своих результатов. Математика — это прежде всего игра ума, жесткое следование причинно-следственным связям. Почти все математические построения сводятся к решению интегральных и дифференциальных уравнений, а те, в свою очередь, с некоторым приближением, решаются нахождением корней многочленов. Здесь мы впервые встречаемся с парадоксом мнимых чисел.
Ученые естествоиспытатели, решая совершенно практические задачи, прибегая к решениям различных уравнением, обнаруживают математические парадоксы. Интерпретация этих парадоксов приводит к совершенно удивительным открытиям. Двойственная природа электромагнитных волн один из таких примеров. Комплексные числа в понимании их свойств играют решающую роль.
Это, в свою очередь, нашло практическое применение в оптике, радиоэлектронике, энергетике и многих других технологических сферах. Еще один пример, гораздо более тяжелый для понимания физических явлений. Антиматерия была предсказана на кончике пера. И только через много лет начинаются попытки ее физического синтезирования.
Не надо думать, что только в физике существуют такие ситуации. Не менее интересные открытия совершаются в живой природе, при синтезировании макромолекул, во время изучения искусственного разума. И все это благодаря расширению нашего сознания, уходу от простого сложения и вычитания натуральных величин.
№15 Основные сведения о комплексных числах.
Комплексным числом называется выражение вида:
где – c обозначение комплексного числа; a и b – соответственно действительная и мнимая части комплексного числа; j=√(-1) – мнимая единица.
Величины a и b часто обозначают следующим образом: a = Re(c) , b = Im(c) . Символы Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый.
Геометрически комплексное число изображается вектором на комплексной плоскости (рис. 15.1). Горизонтальная и вертикальная оси, отмеченные соответственно знаками +1 и +j, называются действительной (или вещественной) и мнимой. Действительная и мнимая составляющие комплексного числа представляют собой проекции вектора на эти оси.
Рис. 15.1 — Вектор на комплексной плоскости
Модуль комплексного числа, равный длине вектора, а
— аргумент комплексного числа. Так как
— тригонометрическая форма комплексного числа. С помощью формулы Эйлера
последняя преобразуется в показательную форму:
Применяется еще и полярная форма
в самой простой форме задающая модуль и агрумент комплексного числа.
Свойства мнимой единицы (рис. 15.2):

Рис. 15.2 — Единичный вектор в комплексной плоскости
Два комплексных числа c и c` называются сопряженными, если они имеют одинаковые модули и равные по величине, но разные по знаку аргументы (рис. 15.3):
Рис. 15.3 — Сопряженный комплексные числа
Изображающие их векторы симметричны относительно вещественной оси.
Действия над комплексными числами.
Сложение и вычитание производится над числами, записанными в алгебраической форме:
т.е. складываются по отдельности вещественные и мнимые части слагаемых:
Операции сложения комплексных чисел соответствует сложение изображающих их векторов.
Сумма сопряженных комплексных чисел равна удвоенному значению вещественной части:
Умножение и деление комплексных чисел удобнее всего производить в показательной форме. Модули при этом перемножаются или делятся, а аргументы складываются или вычитаются:
Что происходит с векторами при перемножении комплексных чисел?
На рис. 15.4 мы видим, что при умножении длина вектора возросла в с2 раз, а аргумент увеличился на α2.Рассматривая комплексное число как вектор, мы приходим к следующему выводу.
При умножении вектора на комплексное число аеjα , вектор растягивается в а раз и поворачивается на угол α .
Рис. 15.4 — Перемножение комплексных чисел
Произведение сопряженных комплексных чисел равно квадрату модуля комплексного числа:
Иногда приходится производить умножение и деление комплексных чисел в алгебраической форме. Перемножение выполняется по правилам умножения многочленов с учетом того, что j2 = -1
При делении, чтобы получить результат, необходимо избавиться от мнимой единицы в знаменателе. Этого можно достичь умножением числителя и знаменателя на сопряженный знаменатель: