По теореме пифагора окружность (6 видео)

Окружность — модель устройства мира

Число Пи ( π ) и Золотая пропорция (φ) связаны абсолютными тождествами (см. Тождественность числа Пи и Золотой пропорции):

При этом 2* π = 360° — это окружность.

Число Пи (выраженное в градусах) — угловая величина и Золотая пропорция – линейная величина, являются различными математическими выражениями одного и того же закона Мироздания, суть которого — целостность и гармоничность мира.

2) Золотая пропорция и уравнение окружности

Золотая пропорция, есть частный случай уравнения окружности x 2 + y 2 = r 2 , при r = 1, а x = y 2 , где x = y 2 – это уравнение параболы (см. Тождественность числа Пи и Золотой пропорции).

Если есть два параметра, числа или явления, связанные между собой Золотой пропорцией, то это говорит о том, что есть также уравнение окружности, включающее в себя эти параметры, т.е. всё, что гармонично, явно или неявно связано функционально через окружность.

3) Теорема Пифагора и окружность

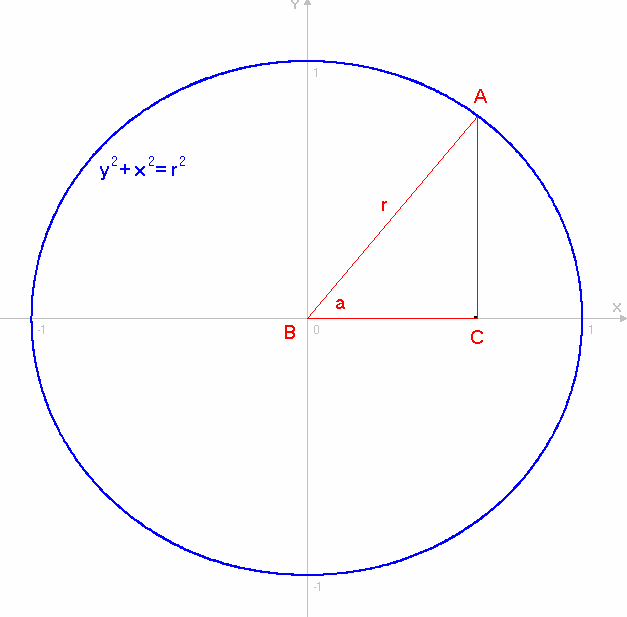
Уравнение окружности задано уравнением x 2 + y 2 = r 2 :

Рассмотрим треугольник ABC:

Т.к. величина ВС равна значению x для точки A, и величина AC равна значению y для точки A, при этом радиус окружности г равен AB, то уравнение окружности x 2 + y 2 = r 2 можно записать в виде:

(ВС) 2 + (AC) 2 = (AB) 2

А это ничто иное, как уравнение прямоугольного треугольника ABC, с катетами AC, ВС, и гипотенузой AB (Теорема Пифагора).

График взаимосвязи параметров x и y, представляет собой, множество всех точек A прямоугольного треугольника ABC, при изменяемых величинах катетов AC, ВС и постоянной величине гипотенузы AB ( r = const ).

4) Окружность и энергия

Число π в угловых единицах измерения — это 180°, и это — ровно половина окружности. Если угол, соответствующий полной окружности — 2 π , обозначить любой другой буквой, например П (П= 2 π = 360°), то уравнение площади круга запишется в виде:

а уравнение периметра окружности запишется в виде:

Сравните полученные формулы с формулой кинетической энергии тела:

и формулой импульса тела:

Не означает ли это принципиальную связь массы тела с числом Пи? Сопоставляя формулы (например, импульса и длины окружности), из размерностей величин входящих в них, можно увидеть, что отношение массы ко времени будет иметь тот же математический смысл, что и число Пи.

p = mV = ml/t, где l — длина, имеющая ту же размерность, что и радиус окружности [м], а t — время [c].

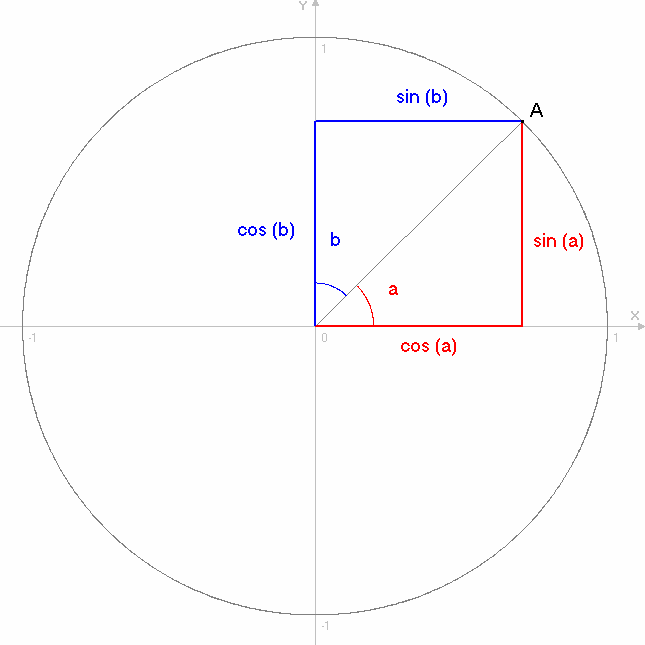
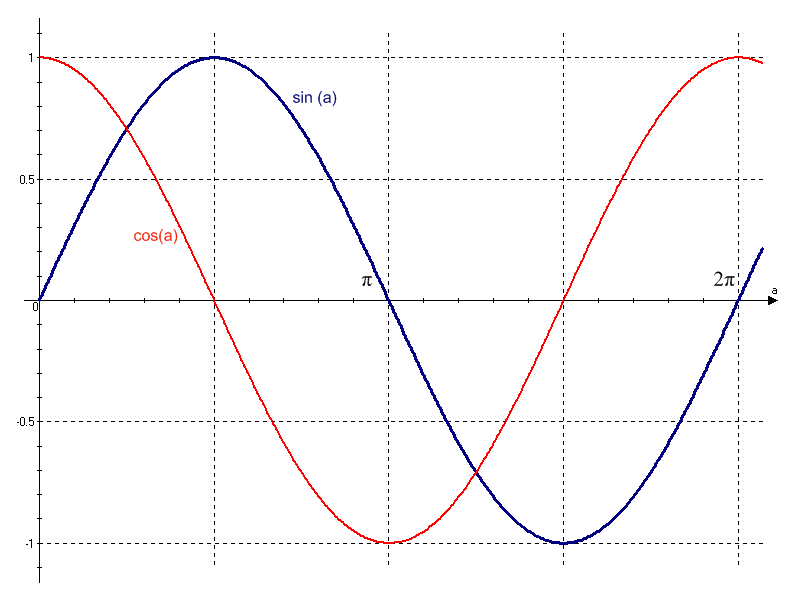
5) Синус, косинус и уравнение окружности

Так как у = sin(a), а x = cos(a), то уравнение окружности с единичным радиусом x 2 + y 2 = 1, можно записать, как:

В этом случае уравнение окружности будет отражать зависимость не от двух параметров х от y, а только от одного — угла a:

Можно перечислить всё, что, так или иначе, связано с окружностью:

Окружность — это геометрическая фигура.

Окружность — это траектория движения, орбита.

Окружность — это цикличность всех процессов происходящих в мире.

Прямая линия, это крайний случай дуги окружности с бесконечным радиусом. Так как этот случай один из бесконечного числа вариантов, и окружность с бесконечным радиусов в пределах нашей, конечной по размерам, Вселенной существовать не может, то можно утверждать, что в мире нет прямых линий, также, как и нет прямолинейного движения.

Уравнение окружности можно представить в виде уравнений синуса и косинуса, поэтому все процессы с параметрами, изменяющиемися, как функция синуса или косинуса (а это — электромагнитные излучения, свет, звук, тепловое излучение, радиоволны, рентгеновское излучение и т.д. и т.п.), т.е. все или почти все процессы во Вселенной, являются частью процессов, изменяющихся по уравнению окружности.

Уравнение, связывающее катеты и гипотенузу прямоугольного треугольника (Теорема Пифагора), есть ни что иное, как уравнение окружности в том виде, что гипотенуза — это радиус окружности, а катеты — это проекции радиуса окружности (гипотенузы) на координатные оси.

Уравнение окружности включает в себе Золотую пропорцию (как частный случай уравнения окружности), и это позволяет связать музыкальную и эстетическую гармонию, а также целостность Вселенной, с окружностью.

Косвенно, на связь с уравнением окружности указывает подобие формул кинетической энергии, импульса тела и формул площади круга и длины окружности.

Окружность в виде сферы – самая распространенная форма во Вселенной. Из всех возможных тел, при условии равенства их объёмов, только сфера имеет самую маленькую площадь поверхности.

И это конечно же, далеко не весь список.

Если человечество когда-либо найдёт универсальное математическое описание всему, что происходит в мире, то нет никаких сомнений, что этим описанием будет формула окружности.

Видео:Лекция 8. Теорема Пифагора и уравнение окружностиСкачать

Окружность. Основные теоремы

Определения

Центральный угол – это угол, вершина которого лежит в центре окружности.

Вписанный угол – это угол, вершина которого лежит на окружности.

Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.

Теорема

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Доказательство

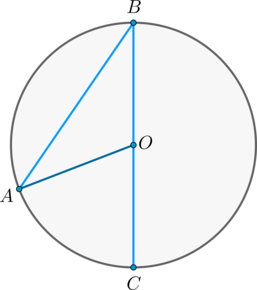
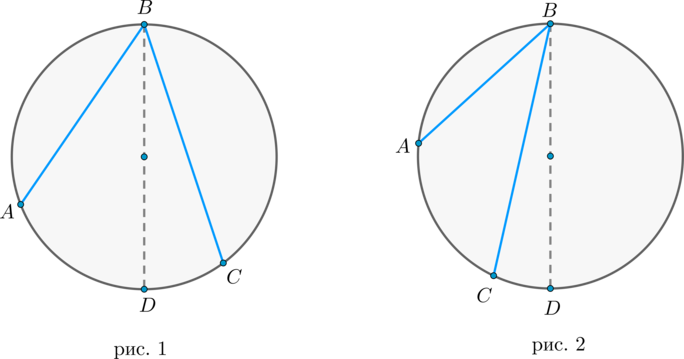
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка (B) – вершина вписанного угла (ABC) и (BC) – диаметр окружности:

Треугольник (AOB) – равнобедренный, (AO = OB) , (angle AOC) – внешний, тогда (angle AOC = angle OAB + angle ABO = 2angle ABC) , откуда (angle ABC = 0,5cdotangle AOC = 0,5cdotbuildrelsmileover) .

Теперь рассмотрим произвольный вписанный угол (ABC) . Проведём диаметр окружности (BD) из вершины вписанного угла. Возможны два случая:

1) диаметр разрезал угол на два угла (angle ABD, angle CBD) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.

2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла (angle ABD, angle CBD) , у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.

Следствия

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2. Вписанный угол, опирающийся на полуокружность, прямой.

3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Определения

Существует три типа взаимного расположения прямой и окружности:

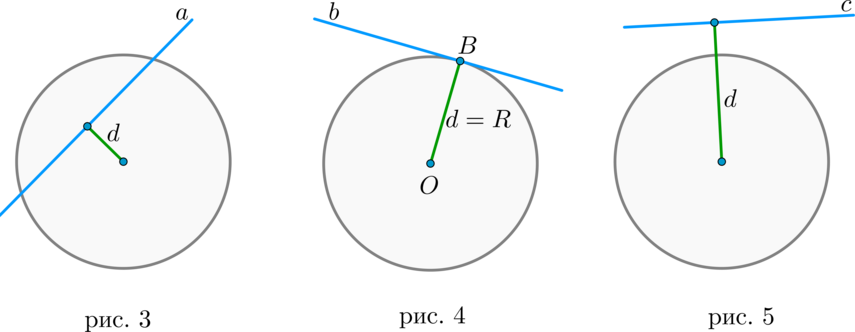
1) прямая (a) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние (d) от центра окружности до прямой меньше радиуса (R) окружности (рис. 3).

2) прямая (b) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка (B) – точкой касания. В этом случае (d=R) (рис. 4).

3) прямая (c) не имеет общих точек с окружностью (рис. 5).

Теорема

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.

Следствие

Отрезки касательных, проведенных из одной точки к окружности, равны.

Доказательство

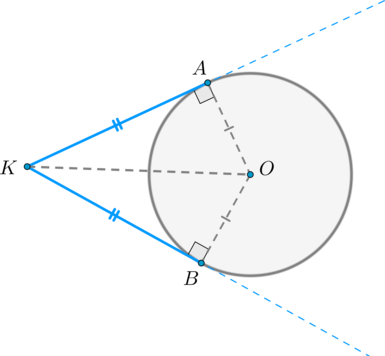
Проведем к окружности из точки (K) две касательные (KA) и (KB) :

Значит, (OAperp KA, OBperp KB) как радиусы. Прямоугольные треугольники (triangle KAO) и (triangle KBO) равны по катету и гипотенузе, следовательно, (KA=KB) .

Следствие

Центр окружности (O) лежит на биссектрисе угла (AKB) , образованного двумя касательными, проведенными из одной точки (K) .

Теорема об угле между секущими

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

Доказательство

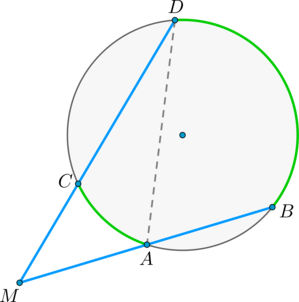
Пусть (M) – точка, из которой проведены две секущие как показано на рисунке:

Покажем, что (angle DMB = dfrac(buildrelsmileover — buildrelsmileover)) .

(angle DAB) – внешний угол треугольника (MAD) , тогда (angle DAB = angle DMB + angle MDA) , откуда (angle DMB = angle DAB — angle MDA) , но углы (angle DAB) и (angle MDA) – вписанные, тогда (angle DMB = angle DAB — angle MDA = fracbuildrelsmileover — fracbuildrelsmileover = frac(buildrelsmileover — buildrelsmileover)) , что и требовалось доказать.

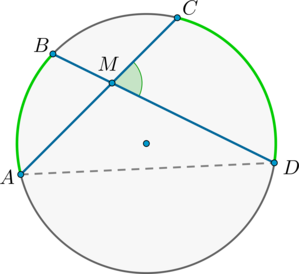
Теорема об угле между пересекающимися хордами

Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: [angle CMD=dfrac12left(buildrelsmileover+buildrelsmileoverright)]

Доказательство

(angle BMA = angle CMD) как вертикальные.

Из треугольника (AMD) : (angle AMD = 180^circ — angle BDA — angle CAD = 180^circ — frac12buildrelsmileover — frac12buildrelsmileover) .

Но (angle AMD = 180^circ — angle CMD) , откуда заключаем, что [angle CMD = frac12cdotbuildrelsmileover + frac12cdotbuildrelsmileover = frac12(buildrelsmileover + buildrelsmileover).]

Теорема об угле между хордой и касательной

Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.

Доказательство

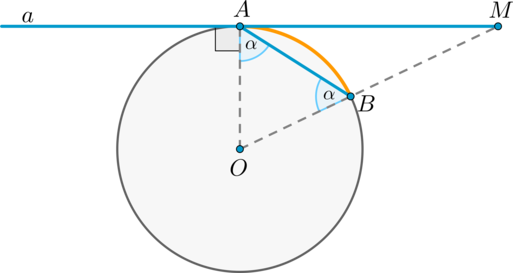
Пусть прямая (a) касается окружности в точке (A) , (AB) – хорда этой окружности, (O) – её центр. Пусть прямая, содержащая (OB) , пересекает (a) в точке (M) . Докажем, что (angle BAM = frac12cdot buildrelsmileover) .

Обозначим (angle OAB = alpha) . Так как (OA) и (OB) – радиусы, то (OA = OB) и (angle OBA = angle OAB = alpha) . Таким образом, (buildrelsmileover = angle AOB = 180^circ — 2alpha = 2(90^circ — alpha)) .

Так как (OA) – радиус, проведённый в точку касания, то (OAperp a) , то есть (angle OAM = 90^circ) , следовательно, (angle BAM = 90^circ — angle OAB = 90^circ — alpha = frac12cdotbuildrelsmileover) .

Теорема о дугах, стягиваемых равными хордами

Равные хорды стягивают равные дуги, меньшие полуокружности.

И наоборот: равные дуги стягиваются равными хордами.

Доказательство

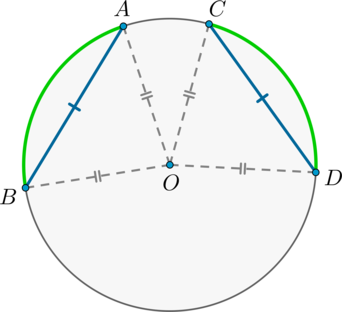
1) Пусть (AB=CD) . Докажем, что меньшие полуокружности дуги (buildrelsmileover=buildrelsmileover) .

(triangle AOB=triangle COD) по трем сторонам, следовательно, (angle AOB=angle COD) . Но т.к. (angle AOB, angle COD) — центральные углы, опирающиеся на дуги (buildrelsmileover, buildrelsmileover) соответственно, то (buildrelsmileover=buildrelsmileover) .

2) Если (buildrelsmileover=buildrelsmileover) , то (triangle AOB=triangle COD) по двум сторонам (AO=BO=CO=DO) и углу между ними (angle AOB=angle COD) . Следовательно, и (AB=CD) .

Теорема

Если радиус делит хорду пополам, то он ей перпендикулярен.

Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.

Доказательство

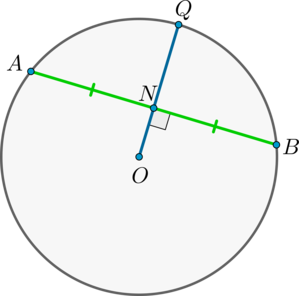
1) Пусть (AN=NB) . Докажем, что (OQperp AB) .

Рассмотрим (triangle AOB) : он равнобедренный, т.к. (OA=OB) – радиусы окружности. Т.к. (ON) – медиана, проведенная к основанию, то она также является и высотой, следовательно, (ONperp AB) .

2) Пусть (OQperp AB) . Докажем, что (AN=NB) .

Аналогично (triangle AOB) – равнобедренный, (ON) – высота, следовательно, (ON) – медиана. Следовательно, (AN=NB) .

Теорема о произведении отрезков хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Доказательство

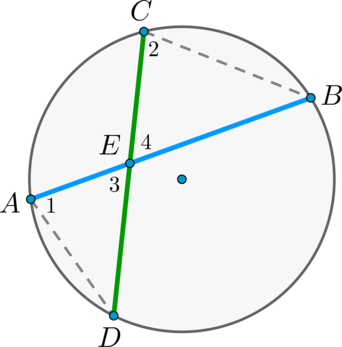
Пусть хорды (AB) и (CD) пересекаются в точке (E) .

Рассмотрим треугольники (ADE) и (CBE) . В этих треугольниках углы (1) и (2) равны, так как они вписанные и опираются на одну и ту же дугу (BD) , а углы (3) и (4) равны как вертикальные. Треугольники (ADE) и (CBE) подобны (по первому признаку подобия треугольников).

Тогда (dfrac = dfrac) , откуда (AEcdot BE = CEcdot DE) .

Теорема о касательной и секущей

Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

Доказательство

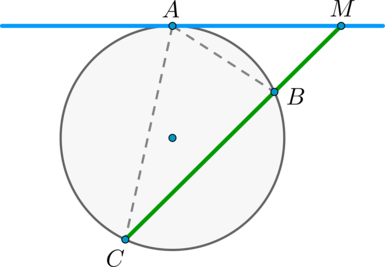
Пусть касательная проходит через точку (M) и касается окружности в точке (A) . Пусть секущая проходит через точку (M) и пересекает окружность в точках (B) и (C) так что (MB . Покажем, что (MBcdot MC = MA^2) .

Рассмотрим треугольники (MBA) и (MCA) : (angle M) – общий, (angle BCA = 0,5cdotbuildrelsmileover) . По теореме об угле между касательной и секущей, (angle BAM = 0,5cdotbuildrelsmileover = angle BCA) . Таким образом, треугольники (MBA) и (MCA) подобны по двум углам.

Из подобия треугольников (MBA) и (MCA) имеем: (dfrac = dfrac) , что равносильно (MBcdot MC = MA^2) .

Следствие

Произведение секущей, проведённой из точки (O) , на её внешнюю часть не зависит от выбора секущей, проведённой из точки (O) :

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Универсальная формула теоремы Пифагора

В прямоугольном треугольнике сумма квадратов катетов равняется квадрату гипотенузы.
(теорема Пифагора)
2 2 2
A + B = C

Эта формула для случая, когда вершина прямого угла треугольника лежит на окружности проходящей через две другие вершины, а гипотенуза является диаметром этой окружности (Рис.2) и является частным случаем другой)(универсальной) формулы:

2 2 2 2 2
A + B + C + D = D (диаметр) Пояснено на Рис.1

Где через круг проведены две перпендикулярные прямые (хорды) и получены четыре а,в,с и d отрезка (катета) — как отрезок от окружности то точки пересечения прямых.
D — диаметр круга.

Формулировка. Если через круг провести две перпендикулярные прямые, то сумма квадратов
четырех полученных отрезков равняется квадрату диаметра.
Также. Из формулы:квадрату диаметра равна сумма квадратов противоположных хорд.
Также легко получается формула площади круга: сумма квадратов перпендикулярных отрезков умноженная на 0.785 что есть 11 деленное на 14.

И, конечно, сумма квадратов хорд (выделено синим на фиг 1) равняется квадрату диаметра.
примечание автора. В литературе такого описания не нашел.
Возможно: в древности она была известна, но забыта.

Доказательства есть. Оно достаточно простое и основано на построениях.