В окружность вписан десятиугольник найдите угол между прямыми

Десятиугольник, вписанный в окружность

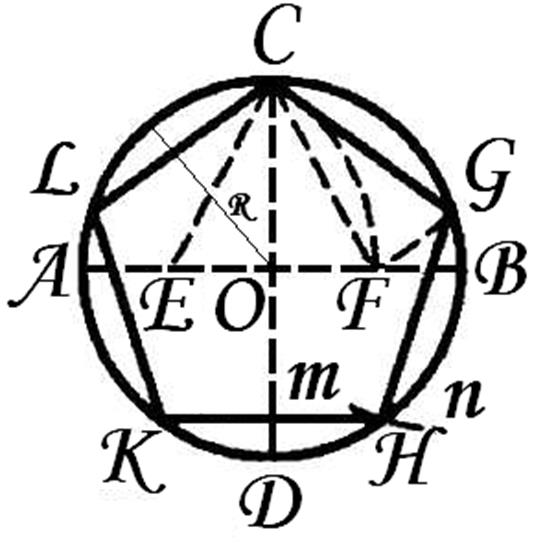
Проводим два взаимно перпендикулярных диаметра АВ и CD. Делим пополам радиус АО в точке Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. OF есть сторона искомой фигуры. С помощью циркуля, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры. Подобно построению пятиугольника, вписанного в окружность.

Десятиугольник, описанный около окружности

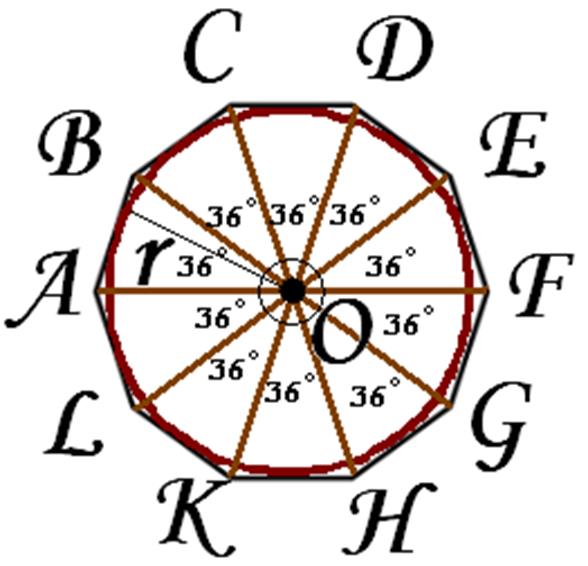
Имеем исходную окружность с центром в точке O. Так как сумма углов, составляющих центральный угол окружности, равна 360°. Делим данный угол на 10 частей (т.к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8924 – | 7231 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

• Как начертить десятиугольник
• Как начертить угол без транспортира
• Как построить правильный восьмиугольник

• – циркуль;
• – линейка.

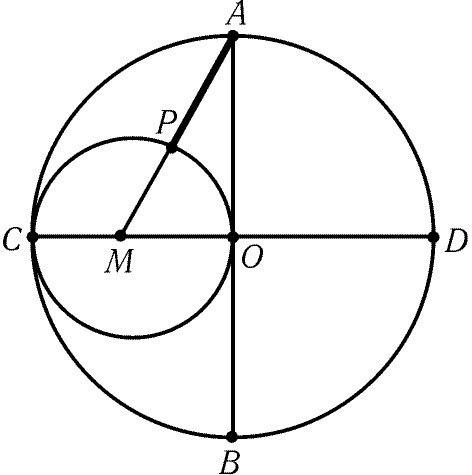
2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.

Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.

Правильный десятиугольник
Сторон и вершин	10
Символ Шлефли
Внутренний угол	144°
Симметрия	Диэдрическая ( D 10 > ), порядок 20.

Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Содержание

Видео:Урок 2. Как найти угол между прямыми || Задание №13. Стереометрия на ЕГЭСкачать

Правильный десятиугольник [ править | править код ]

У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.

Площадь правильного десятиугольника равна (t — длина стороны):

A = 5 2 t 2 c t g π 10 = 5 t 2 2 5 + 2 5 ≈ 7.694 t 2 . >t^ ctg >= > > >>>approx 7.694t^ .>

Альтернативная формула A = 2.5 d t , где d – расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:

d = 2 t ( cos ⁡ 3 π 10 + cos ⁡ π 10 ) , >+cos >
ight),>

и может быть представлен в радикалах как

d = t 5 + 2 5 . >>>.>

Сторона правильного десятиугольника, вписанного в единичную окружность, равна 5 − 1 2 = 1 φ >-1> >= >> , где φ – золотое сечение.

Радиус описанной окружности десятиугольника равен

R = 5 + 1 2 t , >+1> >t,>

а радиус вписанной окружности

r = 5 + 2 5 2 t . >>> >t.>

Построение [ править | править код ]

По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку.

Иначе его можно построить следующим образом:

1. Построить сначала правильный пятиугольник.
2. Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
3. Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Разбиение правильного десятиугольника [ править | править код ]

Гарольдом Коксетером было доказано, что правильный 2 m -угольник можно разбить на m ( m − 1 ) 2 >> ромбов. Для декагона m = 5 , так что он может быть разбит на 10 ромбов.

Видео:В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Пространственный десятиугольник [ править | править код ]

Правильные пространственные десятиугольники
#	#	#

Пентаграммная антипризма с перекрёстом

Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.

У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D_5d [2 + ,10] симметрией порядка 20.

Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники.

Ортогональные проекции многогранников
Додекаэдр	Икосаэдр	Икосододекаэдр	Ромботриаконтаэдр

Многоугольники Петри [ править | править код ]

Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Центральные и вписанные углы

О чем эта статья:

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Видео:10 класс, 21 урок, Угол между прямой и плоскостьюСкачать

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Видео:✓ Экстремальная задача про правильный вписанный многоугольник | Ботай со мной #078 | Борис ТрушинСкачать

В окружность вписан десятиугольник две соседние стороны которого равны радиусу, а остальные 8 сторон равны между собой?

Геометрия | 10 — 11 классы

В окружность вписан десятиугольник две соседние стороны которого равны радиусу, а остальные 8 сторон равны между собой.

Найти сумму наименьшего и наибольшего углов десятиугольника.

Если провести к вершинам 10 — угольника радиусы,

получим равнобедренные треугольники.

Два из них (по условию) окажутся и равносторонними.

В равнобедренном треугольнике углы при основании (это будет сторона 10 — угольника) равны))

наименьший угол 10 — угольника = 120°, наибольший = 150°

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Сумма углов правильного десятиугольника равна ?

Сумма углов правильного десятиугольника равна :

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Для правильного десятиугольника найдите радиус вписанной и описанной окружностей, если его сторона равна 10 см?

Для правильного десятиугольника найдите радиус вписанной и описанной окружностей, если его сторона равна 10 см.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Сторона правильного треугольника равна 12 см?

Сторона правильного треугольника равна 12 см.

Найти радиус вписанной окружности.

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Сторона правильного треугольника равна 12 см?

Сторона правильного треугольника равна 12 см.

Найти радиус вписанной окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Существует квадрат, который не является прямоугольником?

Существует квадрат, который не является прямоугольником?

Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом?

Все диаметры окружности равны между собой?

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Квадрат вписан в окружность радиуса 30√2 см?

Квадрат вписан в окружность радиуса 30√2 см.

Найдите площадь правильного десятиугольника, вписанного в эту же окружность.

Видео:Найдите угол: задача по геометрии с красивым дополнительным построениемСкачать

Углы треугольника соотносятся как 1 : 5 : 6?

Углы треугольника соотносятся как 1 : 5 : 6.

Длина наименьшей стороны равна 2.

Найти радиус вписанной окружности.

Видео:🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Стороны треугольника равны 13, 14, 15?

Стороны треугольника равны 13, 14, 15.

Найти радиус вписанной

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Сумма углов десятиугольника?

Сумма углов десятиугольника?

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Чему равна сумма углов выпуклого : а) десятиугольника ; б) двенадцатиугольника ?

Чему равна сумма углов выпуклого : а) десятиугольника ; б) двенадцатиугольника ?

Вы находитесь на странице вопроса В окружность вписан десятиугольник две соседние стороны которого равны радиусу, а остальные 8 сторон равны между собой? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Простите думала но не получается. Я правда хотела помочь.

180 — 118 = 72 72 : 2 = 36 Это вроде равнобедреный треугольник. Сначало в буквах запиши. А после вот так.

В равнобедренном треугольнике ABC : AB = BC — боковые стороны Основание AC = 12 BD — высота (также медиана и биссектриса), опущенная на основание Пусть BD = x, тогда AB = BC = x + 2 AD = CD = 12 / 2 = 6 (cм) По теореме Пифагора : AB² = BD² + AD² (x +..

Вот тебе подсказка как найти площадь треугольника.

Надеюсь увидишь что там ( всё праверенно).

По моему, вопрос задан неправильно.

Диаметр d = √(4² + (2√5))² = √(16 + 20) = √36 = 6 ; значит радиус r = 3. Длина окружности С = 2πr = 2π * 3 = 6π ; Площадь круга S = πr² = π3² = 9π.

Смотри во вложении.

180(n — 2) = 165n 180n — 360 = 165n 180n — 165n = 360 15n = 360 n = 360 : 15 = 24 Ответ : 24 стороны.

10 задание : Угол САО = 40градусов Угол АСО = 40градусов В треугольнике 180 градусов УГЛЫ САО + АСО = 80 градусов 40 + 40 = 80 градусов Решение : 180 — 80 = 100 градусов УГОЛ СОА = 100 градусов Ответ : 100 градусов.

🎦 Видео

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать