Что такое вектор параметров

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Что такое вектор

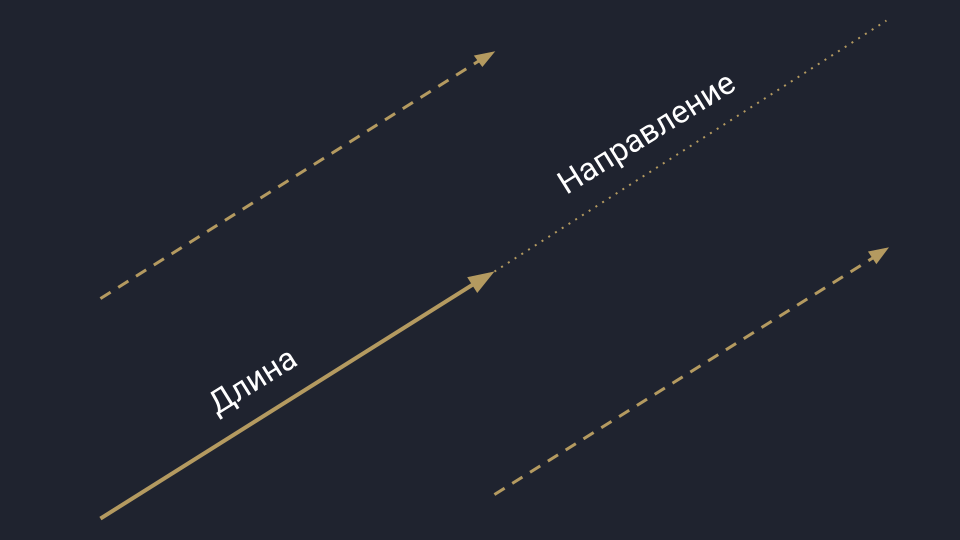
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

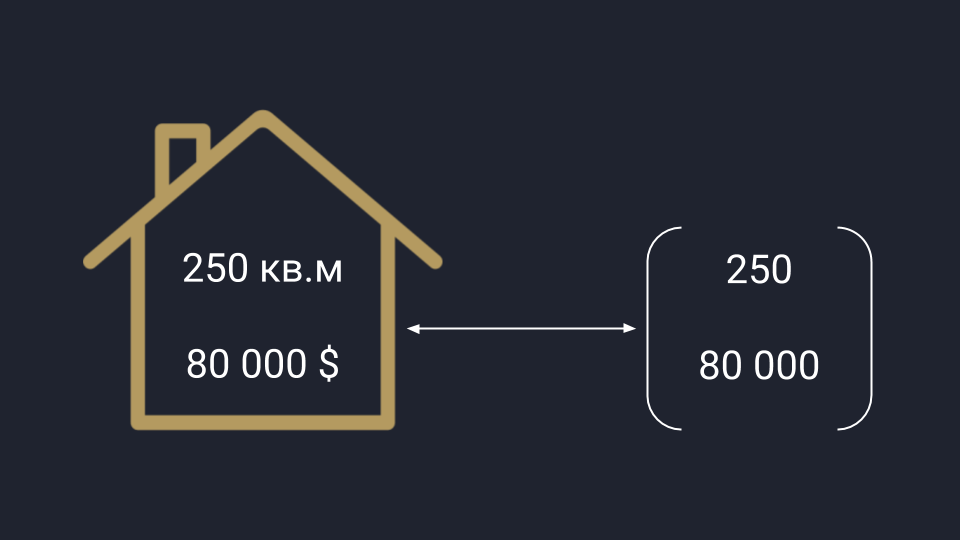
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

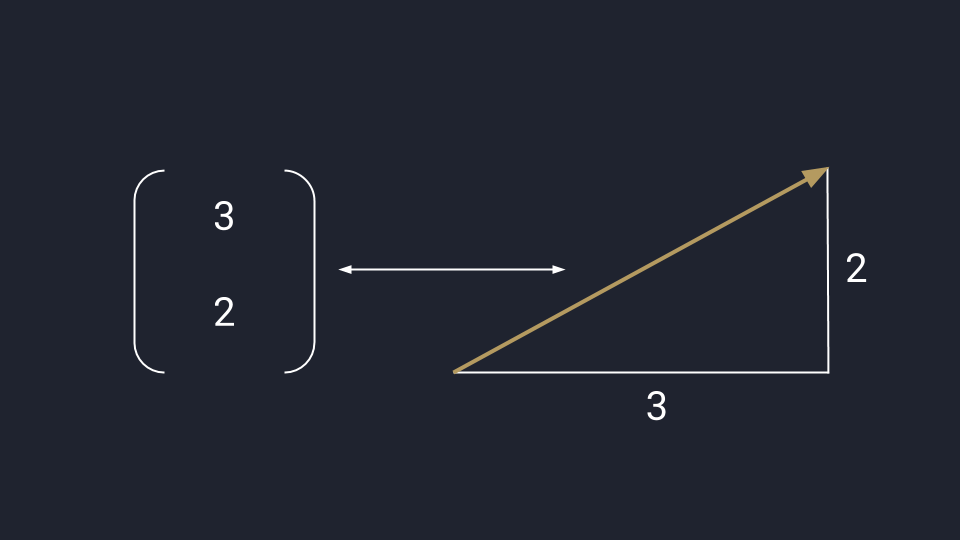
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

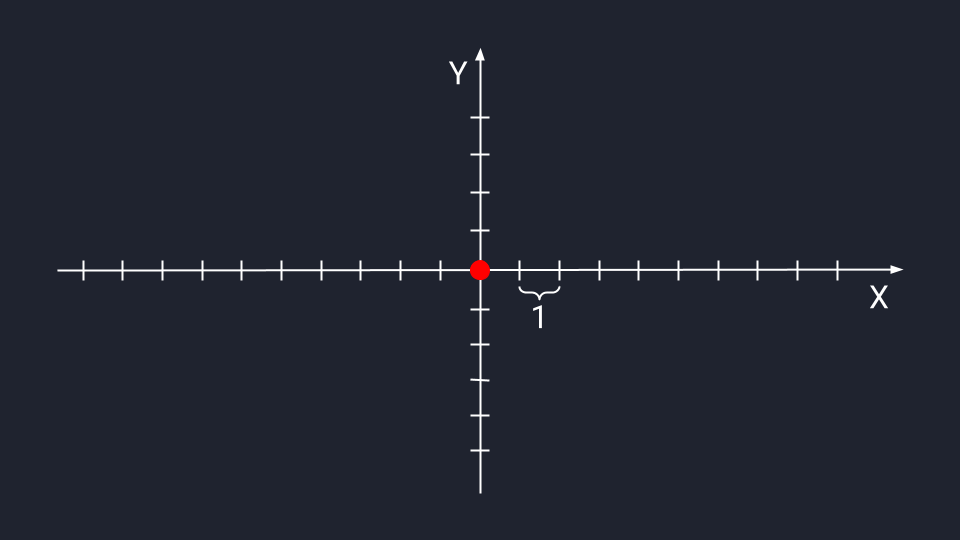
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

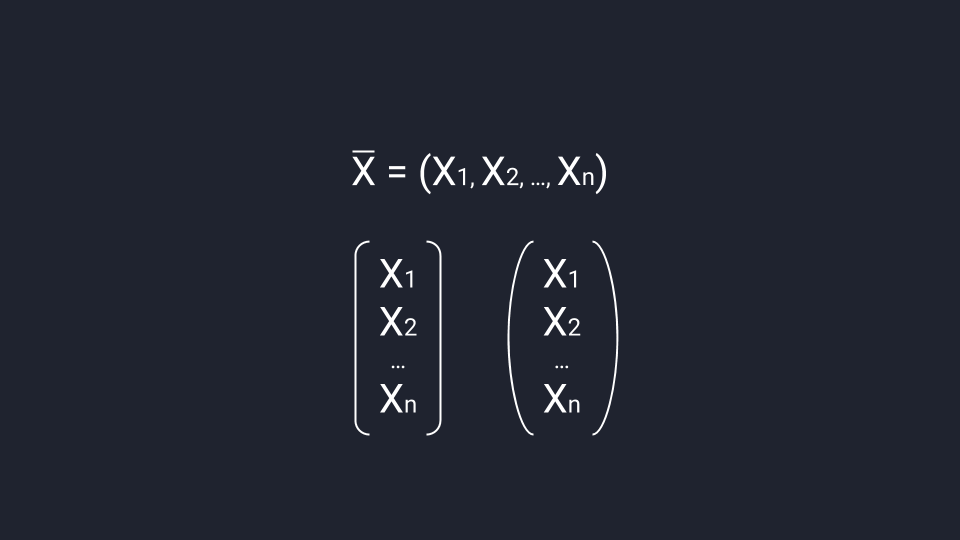
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

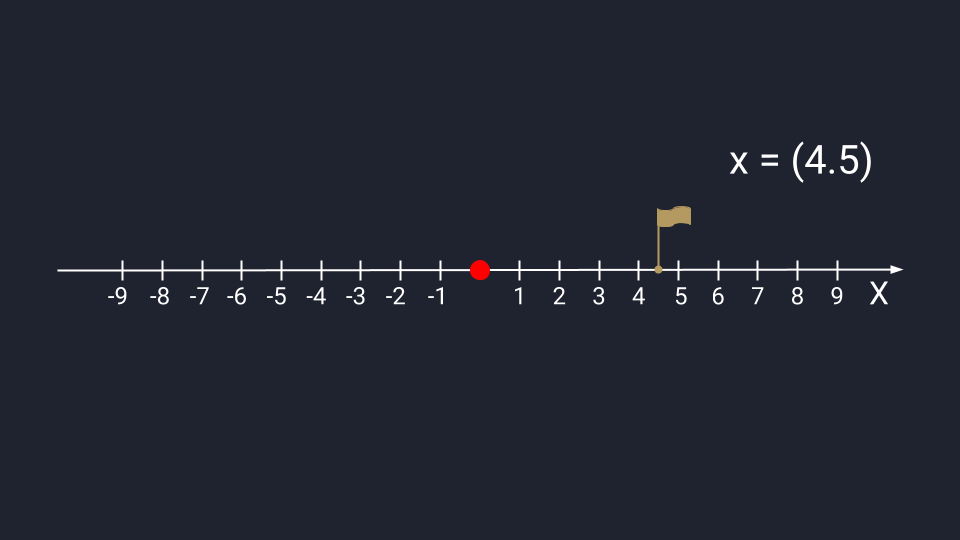
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

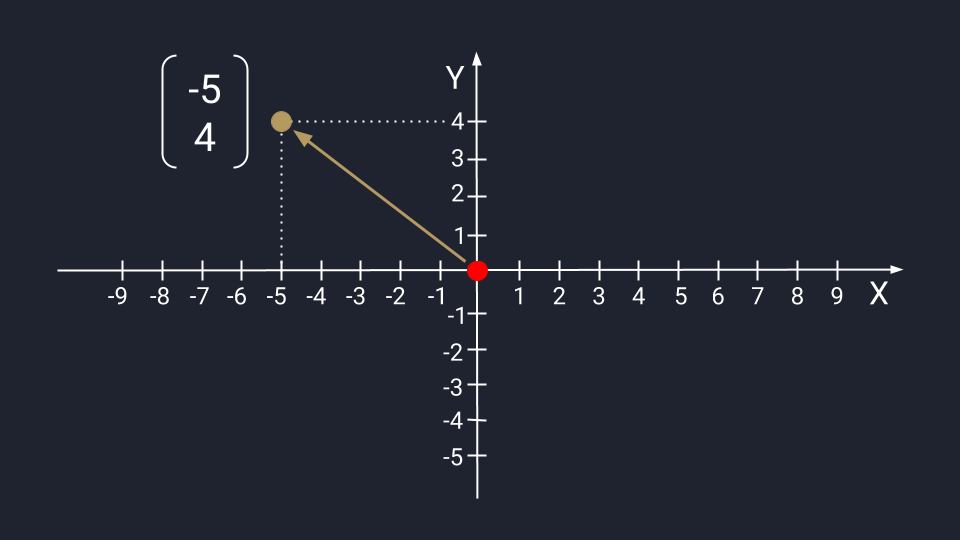
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

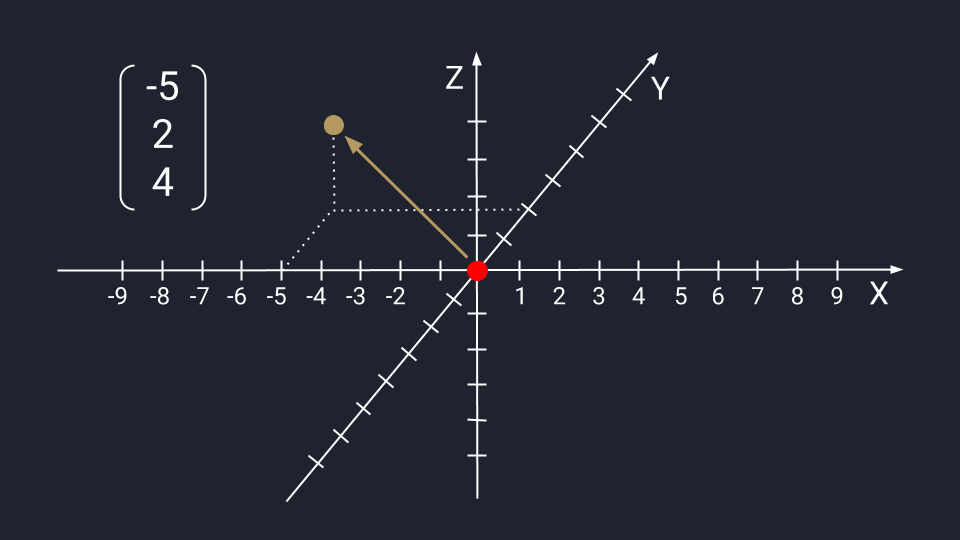
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:8 класс, 40 урок, Понятие вектораСкачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Видео:Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать

Что такое вектор параметров

Свойства производственных функций. Рассмотрим некоторые наиболее общие свойства производственных функций, имеющих форму (2.2), т. е. функций выпуска, допускающих, вообще говоря, замену одного ресурса другим. В этом разделе будут изучены функции с одним продуктом и несколькими ресурсами (трудовыми и материальными). Вектор параметров а в соотношении (2.2) будем опускать, считая, что параметры уже определены и их. влияние нас не интересует. Тогда функция выпуска приобретает вид [c.70]

Р = (Ро Pi. .. Рр) — матрица-столбец, или вектор, параметров размера (р+1) е = (EI EI— л) — матрица-столбец, или вектор, возмущений (случайных ошибок, остатков) размера п. [c.83]

Выше ( 4.2) мы уже показали, что оценка метода наименьших квадратов b = (X X) l X Y есть несмещенная оценка для вектора параметров р, т. е. М(Ь) = р. Любую другую оценку Ь вектора р без ограничения общности можно представить в виде [c.94]

Проверяемая нулевая гипотеза имеет вид — Щ Р =Р» Де )=Дв»)=°2, где Р =Р» — векторы параметров двух моделей е, » — их случайные возмущения. [c.123]

В выражениях 7.2—7.4 вектор-параметр а определяется как оценка широко известного математико-статистического метода наименьших квадратов применительно к уравнениям так называемой простой регрессии, в которой содержится единственная независимая переменная. [c.144]

Обозначим 6 = (бу, 0Й,. . 0 ) — вектор параметров (соответ- [c.76]

Q (дс) — такое множество значений векторов параметров 6 е Q», [c.50]

J 3) — такое множество значений векторов параметров [c.51]

Варьируя вектор параметров а стремятся учесть неравноценность критериев, придавая большее значение той компоненте вектора параметров, которая соответствует критерию большей ценности. Разумеется, никаких строгих определений и рассуждений на этот счет не приводится, поэтому все сказанное можно смело относить к типичным эвристическим приемам. [c.164]

Здесь а — вектор параметров, постоянных на [О, Т], функции fji и fj2 (j = 0. m) непрерывно дифференцируемы по х, а и t и непрерывны по и. [c.324]

Условие (9.59) следует из (9.63) с учетом отсутствия ограничений на х, условия же (9.58) вытекают из того, что по отношению к вектору параметров а задача (9.50), (9.28) является задачей нелинейного программирования, a S — ее функцией Лагранжа. [c.328]

В любом случае на первом этапе определяют оптимальное решение вариационной задачи с точностью до неопределенных параметров. Подставляя это решение в ограничения вариационной задачи, находят уравнения связей между составляющими вектора параметров. Если число таких связей меньше, чем число неопределенных параметров, то, выражая критерий оптимальности через найденное решение, находят целевую функцию от введенных параметров. На втором этапе задача сводится к задаче нелинейного программирования относительно вектора параметров. [c.402]

ММО, использующие целевую функцию (функцию ценности) [92, 87 и др.]. В этих методах предполагается, что структуру предпочтений ЛПР можно формализовать в виде скалярной функции F(y(x), k), где Я, — вектор параметров. Вид функции задается [c.71]

Чтобы решить задачу точечного оценивания, надо найти функцию от наблюдений, которая (в каком-нибудь смысле) наилучшим образом приближала бы параметры рассматриваемой генеральной совокупности. Функция от гипотетических наблюдений, которая используется для приближения (вектора) параметров, называется оценкой. Таким образом, оценка — это случайная величина. Реализовавшееся значение оценки, т.е. то значение, которое получается при подстановке конкретных значений наблюдений, также называется оценкой. [c.318]

Пусть в — рассматриваемый вектор параметров, и в — оценка для в. Тогда ошибка оценки 0 определяется как [c.318]

Пусть функция плотности ф зависит от вектора параметров в. Рассмотрим [c.318]

Линейные ограничения на вектор параметров f3 возникают двояким образом. Во-первых, можно обладать априорной информацией о том, что параметры удовлетворяют определенным линейным ограничениям [c.347]

Вывести, что матрица Л, которая минимизирует ф(Л) есть функция от неизвестного вектора параметров /3, кроме того случая, когда оценка /3 является несмещенной. [c.359]

ФАЗОВОЕ ПРОСТРАНСТВО [phase spa e] — понятие математической теории оптимальных процессов, динамического программирования (пространство состояний) условное математическое пространство, размерность которого определяется числом параметров, характеризующих состояние системы в процессе ее преобразования, управляемого развития. Точка Ф.п. — кортеж, или вектор параметров. Изменение системы описывается перемещением точки по определенной траектории в Ф.п. — она называется фазовой. [c.374]

В основе нейронной сети, называемой динамическим ассоциативным запоминающим устройством (ДАЗУ), лежит идея отображения входных последовательностей в траектории — трубки многомерного сигнального пространства с сохранением топологии пространства перцептивных признаков. Этот принцип, предложенный А.Н. Радченко для интерпретации работы реального нейрона [49] и развитый впоследствии в [50, 51], позволяет построить нейронную сеть, способную к распознаванию речевых образов на основе последовательностей векторов параметров первичного описания сигнала. [c.107]

В качестве метода первичной обработки сигнала для получения вектора параметров был использован метод перцептивного линейного предсказания [55], учитывающий основные особенности психоакустического восприятия и порождения речи, описывающий анализируемый сегмент сигнала пятью параметрами. В качестве шестого параметра использовался регрессионный коэффициент энергии, позволяющий подчеркнуть особенности динамики спектра [56]. [c.115]

В ходе предварительных экспериментов была определена оптимальная длина P (и-грамм) ДАЗУ, равная трем векторам параметров (п = 3). [c.115]

Если в задаче имеется вектор параметров а, то в условия (9.197), (9.198) входит его оптимальное значение а, для которого выполнены условия локальной неулучшаемости функционала L по а [c.382]

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Красивая математика или как представить 7-ми мерный куб

Однажды от своих родственников я услышал такую фразу: «Люди на МехМате МГУ не могут быть нормальными, ведь они могут представить себе 7-ми мерное пространство!»

И когда я это услышал, мне тоже показалось, что это — что-то нереальное, невозможное. Но вот прошли года, и когда я снова услышал эту фразу, меня повергло в шок — я тоже могу представить 7-ми мерное пространство и не сломаться. Или я уже не из тех, кто может спокойно гулять по улицам?

Ответ, казалось бы, так прост и так несложен, но многие просто не задумывались над этим вопросом, и поэтому это кажется чем-то странным и нереальным.

Так вот, в данной статье я хочу задуматься, ответить и рассказать, что же за простой ответ скрывается под таким странным вопросом: «Что такое 7-ми мерное пространство?»

В данной статье я попытаюсь рассказать свое понимание многомерного пространства, как я представляю его в своей голове. Возможно, что-то может показаться немного нестрогим – так оно и есть, понятное дело, я пропускаю некоторые детали и пытаюсь писать максимально научно-популярным языком. Надеюсь, Вам понравится мое видение многомерного пространства и Вы почувствуете ту же красоту математики, которую я вижу в данной иллюстрации чего-то непонятного.

Я постараюсь описать некоторые детали с самых азов, вкратце, чтобы любой желающий мог бы разобраться в моих словах.

Видео:Вектор: Зачем Он Нужен. Что Такое Вектор? Palsan Показал свое лицо.Скачать

Оглавление

Выражаю благодарность @AnnRemi за помощь в редактировании и опускании на землю моих амбиций по статье.

Видео:Тема: Движения. Урок: Что такое векторыСкачать

Начало начал, или что такое вектор

Вектор: наверняка каждый сталкивался с таким понятием в школе, это не сложно и очень понятно.

Вектором называется направленный отрезок или просто луч, имеющий конкретную длину.

То есть если луч, как и прямая — понятие бесконечное и простирается вправо и влево в бесконечность, то вектор — понятие ограниченное длиной. Обычная стрелочка, нарисованная на бумаге — вектор. Линейкой мы можем измерить длину этой стрелочки, а направление «этой длины» показывает сама стрелка. Важно понимать, что нам не важно, откуда отложен наш вектор, из какой точки. Нужно знать только длину и направление. Обычно мы изображаем наш вектор в осях координат — так удобно находить его параметры.

Вектор AB в осях координат

Для удобства мы отмечаем на оси Х и на оси У проекции наших точек. Теперь, чтобы посчитать длину нашего вектора достаточно воспользоваться Теоремой Пифагора

Направление, или угол наклона относительно оси Х легко посчитать, например, через тангенс, ведь мы знаем длины обоих катетов треугольника

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Понятие радиус-вектора

Как мы уже увидели, в векторе нам важны только две вещи: длина и направление, так зачем его рисовать где-то в середине нашей координатной плоскости. Давайте сместим наш вектор к началу оси координат. Тогда нам надо будет хранить только координаты конца вектора — а координаты начала вектора у нас будут нулевыми.

Смещенная ось координат

Так теперь надо будет меньше мучаться — храним в векторе просто координаты его конца.

Такие вектора называются в школе радиус-векторами, но в дальнейшем мы будем все вектора брать радиус-векторами, ведь, как мы помним, все вектора имеющие одно направление и одну длину — одинаковые, один и тот же вектор, так почему бы нам не взять тот, который удобнее всего записывается.

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Трехмерный вектор

Если мы уже разобрались, что такое вектор на плоскости — давайте перейдем к вектору в трехмерном пространстве — в объемном мире.

Достаточно просто представить себе стрелку в объеме — достаточно вспомнить, как Вы что-то измеряли рулеткой. Прислонили конец к шкафу, другой к полу, и померили его диагональ. Ну или не шкаф. каждому свое. Но точно можно сказать, что такое трехмерный вектор.

Но давайте немного формулизируем то, что мы поняли. Представим трехмерные координаты и в них наш радиус-вектор AB.

Трехмерный вектор AB

Понятно, что нам теперь совсем не хватит двух координат для описания вектора AB. Так что давайте добавим третью координату, просто дописав ее в конце.

Хммм. интересно, а по какому признаку мы можем вот так просто приписывать координаты? Может, можно просто так добить вектор до семимерного? Ну в принципе, нас никто остановить не может, и мы именно так и поступим, но сначала немного окунемся в линейную алгебру.

Видео:Радиус векторСкачать

Базис в пространстве

Базис — упорядоченный набор векторов в векторном пространстве, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора.

Линейная комбинация – это сумма некоторого набора элементов множества с допустимыми коэффициентами.

Также я собираюсь использовать в дальнейшем удобное следствие определения базиса: мы можем расширять наш базис с помощью векторов, линейно независимых с базисными.

Что значит расширить базис? Добавить еще один вектор, тем самым расширяя наше пространство еще в одном направлении.

Выше мы уже научились строить трехмерное пространство — просто объемный мир, в котором мы живем. Давайте попробуем расширить наш базис. Самым очевидным расширением базиса будет добавление времени, как еще одного параметра. То есть четырехмерное измерение — это объемная жизнь с привязкой ко времени. Ну разве это не похоже на обычную жизнь человека? То есть все это время мы жили в четырехмерном пространстве, а не трехмерном.

И, как не сложно заметить, время линейно независимо от объема, то есть наше расширение базиса вполне корректно.

Видео:ЧТО ТАКОЕ ВЕКТОР? // 9 класс // геометрияСкачать

7ми мерное пространство и почему только 7ми?

Как нам представить 5ти мерное пространство? Но мы же уже сказали, что на самом деле пространство — это то, что его задает — базис. То есть давайте теперь мыслить о пространстве, как о наборе параметров каждой его точки. Например для трехмерного объекта мы помним 3 координаты в пространстве — по x, y, z. И у нас это не вызывает диссонанса.

Давайте к координатам припишем еще и время, в которое у нас наблюдалась данное расположение тел. Например, у нас катится шар и мы следим за положением его центра. В момент времени 0 шар покоился. В 0,0. 01 он уже сместился. В момент времени 9. 9,0 он уже находится в совершенно другом месте. Но зачем нам так думать? Пусть эта точка шара существует одновременно везде, где проехался шар, только мы будем помнить, что в каждой точке мы еще приписываем время, когда шар был именно в данной позиции. Вот Вам и 4х мерное пространство — не сложно.

Казалось, так можно навесить еще какие-то параметры, такие как скорость ветра, влажность воздуха, сила трения и так далее, но давайте не будем извращаться и перейдем к более жизненному понятию.

Допустим у нас есть разные гаечки (прошу прощения, если я ошибусь в параметрах или названиях, я совсем не инженер). Для удобной фасовки и продажи гаек надо распределить их на группы одинаковых. Но как мы будем их отличать? Давайте запишем какой-то набор параметров (не претендующий на правильность):

Сплав метала гайки

Внутреннее сечение гайки

Внешняя форма гайки

Направление резьбы гайки

Максимальная нагрузка на гайку

Самозажимающаяся ли гайка?

Максимальная температура, при которой гайка выдерживает достаточную нагрузку

Понятно, что таких параметров может быть сколь угодно много. Но мы остановимся на 7ми — именно столько заявлено в заголовке статьи. Важно помнить! каждый параметр обязан быть независим от любого предыдущего. В нашем случае это условие выполняется: направление резьбы никак не зависит от сплава метала или от внутреннего сечения гайки. И так с каждым из параметров.

То есть только что мы создали свой, очень странный базис, где элементами нашего пространства выступают гайки, и мы их можем удобно расфасовать. Это и есть элементарное представление нашего 7ми и не только 7ми, но и большего, пространства.

Видео:Что такое вектор? | Коллинеарные векторы | Сонаправленные векторы | МегаШколаСкачать

Пространство — не куб!

В заголовке статьи я обещал куб, но пока говорил только о пространстве. Давайте определим, что же такое куб.

Например, в 2х мерном пространстве куб, очевидно,- это квадрат. То есть объект с точками вершинами:

В трехмерном пространстве куб — есть куб. С координатами:

Как мы заметили, в двумерном пространстве у куба 4 = 2^2 вершин, в трехмерном 8 = 2^3. Совпадение? Маловероятно. Ну и правильно, ведь из простейшей комбинаторики мы помним, что количество вершин равно 2^n для n-мерного куба. Ведь мы либо берем каждый из базисных n векторов, либо нет.

Тогда для построение 7ми или n-мерного куба нам достаточно взять точки с фиксированными координатами (0 или a) по каждой из осей.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Интересный факт

Именно из-за удобства понимания и описания n-мерного куба мы меряем любую n-мерную поверхность таким способом. Площадь квартиры с помощью квадратных метров, длину прямой в метрах, объем в кубических метрах. Это все кубы разной размерности. И в математике нам очень удобно оперировать именно такими понятиями. Примерно так мы определяем меру множества, которая очень важна для теории интегралов, теории вероятностей, теории меры и очень много где еще.

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Послесловие

Как Вы, наверное, заметили, я привожу совсем иное понимание многомерного куба, в отличие от общепринятого.

Не то, чтобы красивые картинки многомерных кубов не вызывали у меня восхищения – совсем нет, но в этом есть что-то нереальное, непонятное и неприложимое. Я совсем не претендую на прикладное значение сортировки гаек, но мне кажется довольно захватывающим такое представление многомерности: как что-то такое далекое может быть таким емким.

4х мерный куб – Тессеракт

На самом деле я просто не имею настолько развитого пространственного воображения: я не понимаю, как можно визуализировать 4х, 5ти и более мерный куб на 2D картинке.

Также такая иллюстрация не позволяет представить, как увеличить пространство еще в одном направлении. Так что именно данная тема не рассматривается в моей статье, но, если Вас заинтересовал Тессеракт, есть огромная куча других, очень интересных, статей, описывающих его построение и даже расширение.

🔍 Видео

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Найдите разложение вектора по векторам (базису)Скачать

Коллинеарные векторы.Скачать