Площадь многоугольника равна произведению полупериметра на радиус вписанной окружности

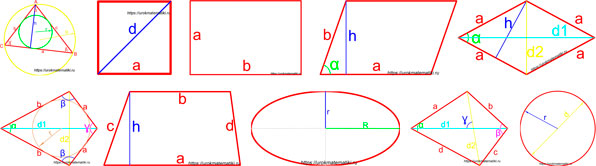
Какие из следующих утверждений верны?

1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.

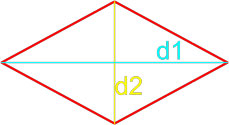
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.

3) Площадь трапеции меньше произведения суммы оснований на высоту.

4) Площадь прямоугольного треугольника меньше произведения его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.» — неверно, площадь многоугольника равна произведению половине периметра на радиус вписанной окружности.

2) «Если диагонали ромба равна 3 и 4, то его площадь равна 6.» — верно, площадь ромба равна половине произведения диагоналей.

3) «Площадь трапеции меньше произведения суммы оснований на высоту.» — верно, площадь трапеции равна половине произведения суммы оснований на высоту.

4) «Площадь прямоугольного треугольника меньше произведения его катетов.» — верно, площадь прямоугольного треугольника равна половине произведения катетов.

Видео:Площадь многоугольника через радиус вписанной окружностиСкачать

Формула площади правильного многоугольника

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Правильный многоугольник так же называют правильным n-угольником , где n — это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).

В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью .

Около любого правильного многоугольника можно описать окружность.

Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.

Видео:Геометрия Доказательство Площадь многоугольника, описанного около окружности равна произведению егоСкачать

Формулы площадей фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p — a p — b p — c ,

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,

где a, b — стороны треугольника,
γ — угол между сторонами a и b .

Формула площади треугольника по трем сторонам и радиусу описанной окружности

a, b, c — стороны треугольника,
R — радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы площади квадрата

Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны.

где S — площадь квадрата,
a — длина стороны квадрата.

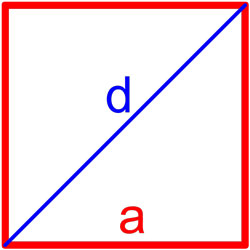
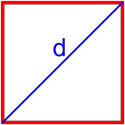
Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

где S — площадь квадрата,
d — длина диагонали квадрата.

Видео:Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон.

где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.

Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Формулы площади параллелограмма

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.

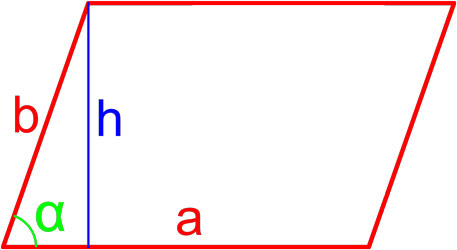
Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.

Формула площади параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.

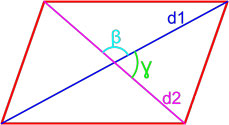
Формула площади параллелограмма по двум диагоналям и углу между ними

Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,

где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.

Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Формулы площади ромба

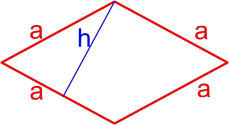
Формула площади ромба по длине стороны и высоте

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.

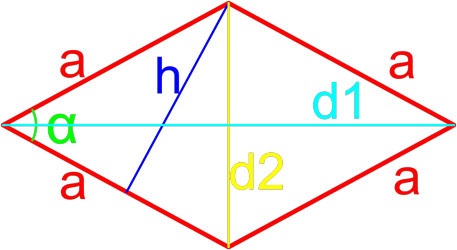
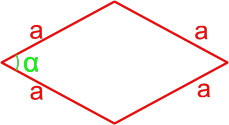
Формула площади ромба по длине стороны и углу

Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.

Формула площади ромба по длинам его диагоналей

Площадь ромба равна половине произведению длин его диагоналей.

где S — площадь ромба,
d1, d2 — длины диагоналей ромба.

Видео:Геометрия Доказательство Площадь треугольника равна произведению его полупериметра и радиусаСкачать

Формулы площади трапеции

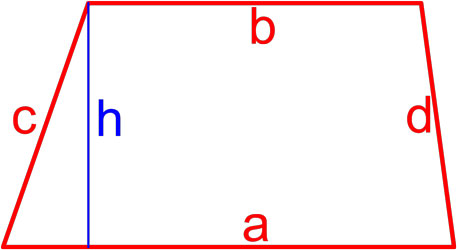
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).

Формула Герона для трапеции

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.

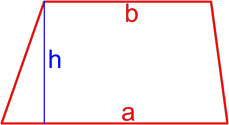
Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы её оснований на высоту.

где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.

Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Формулы площади дельтоида

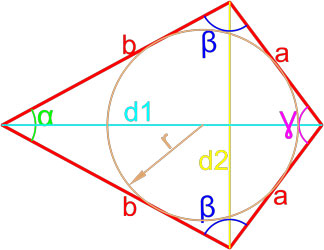
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.

Формула площади дельтоида по двум неравным сторонам и углу между ними

Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.

Формула площади дельтоида по равным сторонам и углу между ними

Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.

S = a 2 sin γ + b 2 sin α 2 ,

где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .

Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности

Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.

Формула площади дельтоида по двум диагоналям

Площадь дельтоида равна половине произведения длин двух диагоналей.

где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.

Видео:Площадь описанного многоугольникаСкачать

Формулы площади произвольного выпуклого четырехугольника

Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними

Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.

S = d1 · d2 · sin γ 2 ,

где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.

Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

Формула площади вписанного четырехугольника (формула Брахмагупты)

Если вокруг четырехугольника можно описать окружность, то его площадь равна

S = p — a p — b p — c p — d ,

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной окружностью

Если в четырехугольник можно вписать окружность, то его площадь равна:

где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной и описанной окружностями

Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.

Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Формулы площади круга

Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи.

S = π r 2 ,

где S — площадь круга,
r — радиус круга.

Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S — площадь круга,
d — диаметр круга.

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Площадь сегмента круга

Площадь кругового сегмента через угол в градусах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.

Площадь кругового сегмента через угол в радианах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

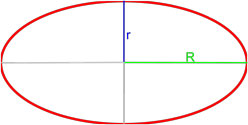
Формула площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.

🎦 Видео

ПЛОЩАДЬ описанного многоугольника Это просто!Скачать

Площадь описанного многоугольникаСкачать

Быстрый способ ➜ Найдите площадь многоугольника на рисункеСкачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Задание 24 Площадь описанного треугольникаСкачать

Радиус вписанной окружности #математика #егэ #математикапрофиль2023 #fyp #школаСкачать