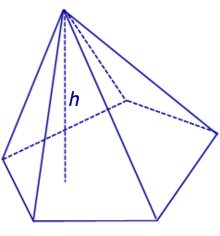
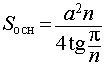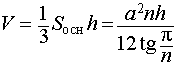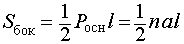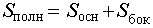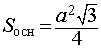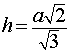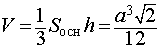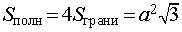- 1. Площадь полной поверхности куба
- 2. Найти площадь поверхности прямоугольного параллелепипеда
- 3. Найти площадь поверхности шара, сферы
- 4. Найти площадь боковой и полной поверхности цилиндра
- 5. Площадь поверхности прямого, кругового конуса
- Нахождение площади правильной пирамиды: формулы
- Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- Пирамиды. Правильные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды
- Пирамиды
- Правильные пирамиды. Свойства правильной пирамиды
- Тетраэдры. Правильные тетраэдры
- Формулы для объема, площади боковой и полной поверхности пирамиды
- 🌟 Видео
Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

1. Площадь полной поверхности куба
a — сторона куба
Формула площади поверхности куба,(S):
Видео:Задание №690 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

2. Найти площадь поверхности прямоугольного параллелепипеда
a , b , c — стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
Видео:10 класс, 33 урок, Правильная пирамидаСкачать

3. Найти площадь поверхности шара, сферы
R — радиус сферы
Формула площади поверхности шара (S):
Видео:🔴 Стороны основания правильной шестиугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

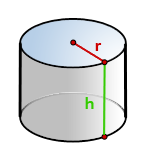
4. Найти площадь боковой и полной поверхности цилиндра
r — радиус основания
h — высота цилиндра
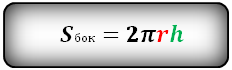
Формула площади боковой поверхности цилиндра, (S бок ):
Формула площади всей поверхности цилиндра, (S):
Видео:Площадь поверхности пирамиды | Геометрия 11 классСкачать

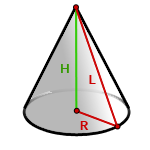
5. Площадь поверхности прямого, кругового конуса
R — радиус основания конуса
H — высота
L — образующая конуса
Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S бок ):
Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S бок ):
Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):
Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Нахождение площади правильной пирамиды: формулы
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать
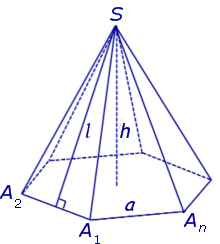
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
1. Через длину основания (a) и высоту (h):
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
Видео:Пирамиды, в которых высота проходит через центр вписанной в основание окружностиСкачать
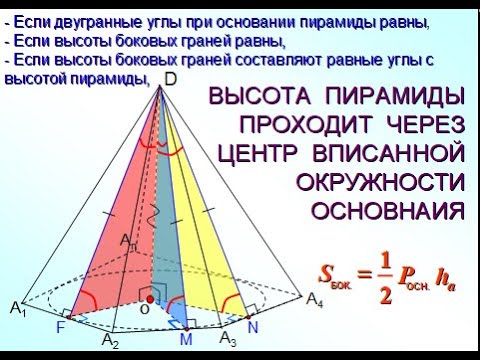
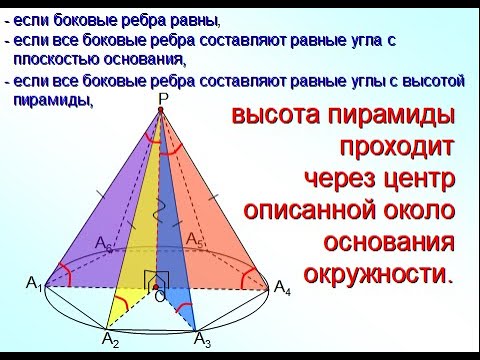
Пирамиды. Правильные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды
 Пирамиды. Теорема Эйлера для пирамид Пирамиды. Теорема Эйлера для пирамид |
 Правильные пирамиды. Свойства правильной пирамиды Правильные пирамиды. Свойства правильной пирамиды |
 Тетраэдры. Правильные тетраэдры Тетраэдры. Правильные тетраэдры |
 Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды |
Видео:10 класс — Задачи на площади боковой и полной поверхности пирамидыСкачать
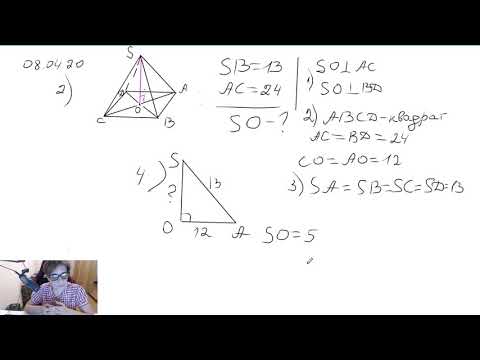
Пирамиды
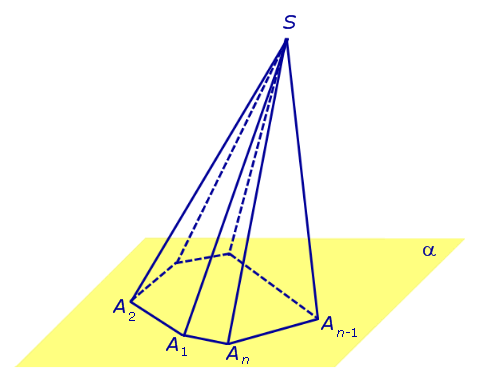
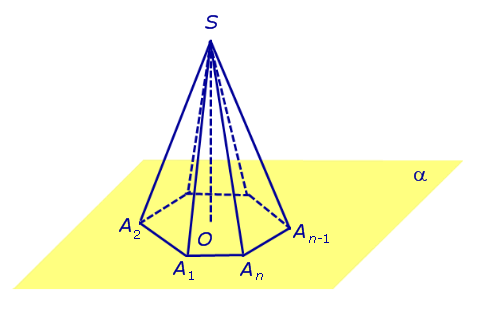
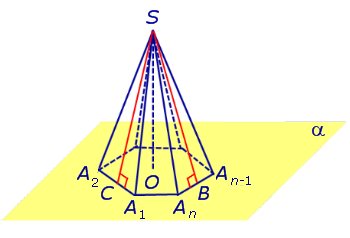
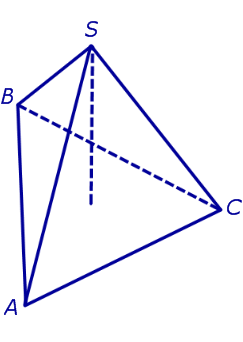
Рассмотрим произвольную плоскость α , произвольный выпуклый n – угольник A1A2 . An , расположенный в этой плоскости, и точку S , не лежащую в плоскости α .
Определение 1. Пирамидой ( n — угольной пирамидой) называют фигуру, образованную отрезками, соединяющими точку S со всеми точками многоугольника A1A2 . An (рис. 1) .
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
| + |
| – |
| = | 2 |
| + |
| – |
| = | 2 |
| + |
| – |
| – |
| = | 2 |
Доказательство. Заметим, что у n — угольной пирамиды (n + 1) вершина, n боковых граней, 1 основание, n ребер основания и n боковых ребер. Следовательно, у n — угольной пирамиды (n + 1) грань и 2n ребер.
то теорема Эйлера доказана.
Видео:#130. Задание 8: комбинация телСкачать

Правильные пирамиды. Свойства правильной пирамиды
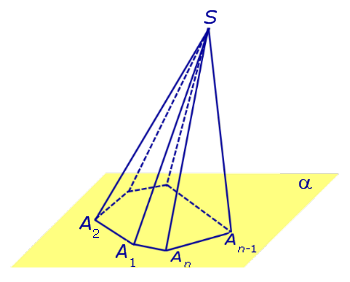
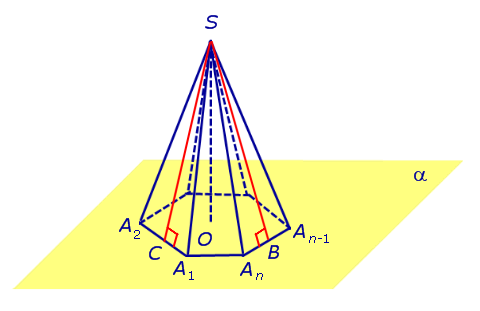
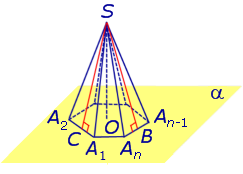
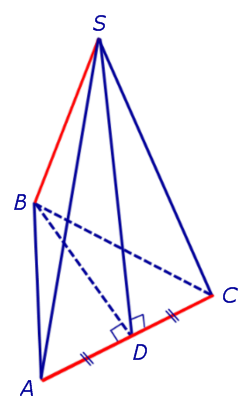
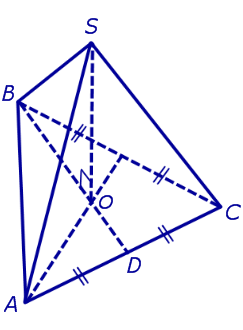
Замечание 2. Если центр основания A1A2 . An правильной пирамиды SA1A2 . An обозначить буквой O , то длина отрезка SO будет равняться высоте пирамиды. Часто и сам отрезок SO называют высотой пирамиды, опущенной из вершины S .
Определение 4. Высоту боковой грани правильной пирамиды, опущенную из вершины S , называют апофемой .
На рисунке 3 отрезок SB – апофема грани SAnAn-1 и отрезок SC – апофема грани SA2A1 .
Замечание 3 . У любой правильной n – угольной пирамиды можно провести n апофем.
Свойства правильной пирамиды:
 | ||
 | ||
 | ||
 |  |
| V | объем пирамиды |
| Sбок | площадь боковой поверхности пирамиды |
| Sполн | площадь полной поверхности пирамиды |
| Sосн | площадь основания пирамиды |
| Pосн | периметр основания пирамиды |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности пирамиды :
| Пирамида | Рисунок | Формулы для объема, площади боковой и полной поверхности |
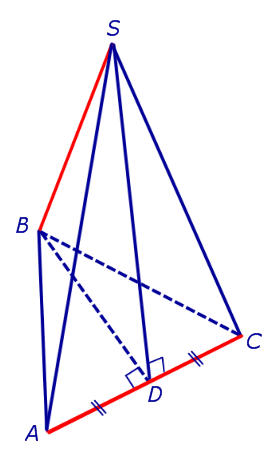
| Произвольная пирамида |  | |
| Правильная n – угольная пирамида | 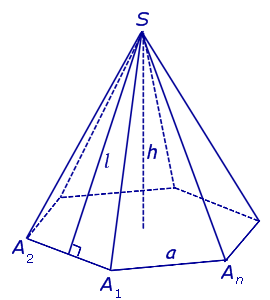 | |
| Правильный тетраэдр |  |
| Произвольная пирамида |

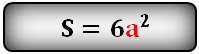



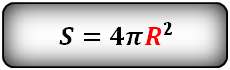










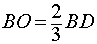
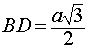 ,
,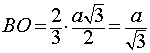 .
.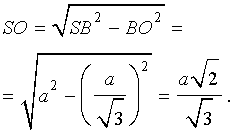
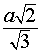
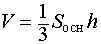 ,
,