Окружность проходит через вершины большей боковой стороны прямоугольной трапеции

Окружность с центром O, расположенном внутри прямоугольной трапеции ABCD, проходит через вершины B и C большей боковой стороны этой трапеции и касается боковой стороны AD в точке T.

а) Докажите, что угол BOC вдвое больше угла BTC.

б) Найдите расстояние от точки T до прямой BC, если основания трапеции AB и CD равны 4 и 9 соответственно.

а) Угол BTC вписан в окружность, а угол BOC — соответствующий ему центральный угол. Следовательно, ∠BOC = 2∠BTC.

б) Из условия касания окружности и стороны AD следует, что прямые OT и AD перпендикулярны. Пусть окружность вторично пересекает прямую AB в точке L и сторону CD — в точке M. Тогда диаметр окружности, перпендикулярный стороне AB, делит каждую из хорд BL и CM пополам. Обозначим OT = r, тогда

По теореме Пифагора По теореме о касательной и секущей Следовательно,

Аналогично

Из теоремы синусов следует, что BC = 2r · sin&nbsp∠BTC. Пусть h — искомое

расстояние от точки T до прямой BC . Выразим площадь треугольника BTC двумя способами:

Отсюда получаем, что Следовательно,

Заметим, что AL больше радиуса окружности, а DC меньше диаметра, поэтому DC Ответ: 6.

Видео:Найти длину верхнего основания и боковой стороны прямоугольной трапецииСкачать

Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T ?

Геометрия | 10 — 11 классы

Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T .

Б) Найдите расстояние от точки T до прямой BC , если основания трапеции AB и CD равны 4 и 9 соответственно.

Если продлить боковые стороны до пересечения в точке E, и обозначить

EC * sin(α) = CD = 9 ;

EB * sin(α) = AB = 4 ;

если перемножить, получится

EB * EC * (sin(α)) ^ 2 = 9 * 4 = 36 ;

ЕB * EC = ET ^ 2 ; и расстояние h от T до BC равно h = ET * sin(α) ; поэтому

Видео:🔴 В прямоугольной трапеции основания ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Окружность радиуса 6 вписана в равнобедренную трапецию?

Окружность радиуса 6 вписана в равнобедренную трапецию.

Точка касания окружности с боковой стороной трапеции делит эту сторону в отношении 1 : 4.

Через центр окружности и вершину трапеции проведена прямая.

Найдите площадь треугольника отсекаемого от этой трапеции данной прямой.

Видео:Геометрия В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит черезСкачать

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC ?

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC .

Окружность проходит через точки C и D и касается прямой AB в точке E.

Найдите расстояние от точки E до прямой CD, если AD = 4, BC = 3.

Видео:Задание 24 ОГЭ по математике #3Скачать

Около окружности описана прямоугольная трапеция?

Около окружности описана прямоугольная трапеция.

Расстояния от центра окружности до концов боковой стороны равны 15см и 20см.

Найдите основания и площадь трапеции.

Видео:ОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC?

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC.

Окружность проходит через точки C и D и касается прямой AB в точке E.

Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 12.

Видео:№17. Профильный ЕГЭ. Планиметрическая задача. ТИП 2Скачать

В прямоугольной трапеции ABCD меньшее основание равно меньшей боковой стороне?

В прямоугольной трапеции ABCD меньшее основание равно меньшей боковой стороне.

Диагональ, проведённая из вершины тупого угла, перпендикулярна большей боковой стороне, равной 8√2 см.

Найдите периметр и площадь трапеции.

Видео:№481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 смСкачать

Окружность проходит через вершины C и D прямоугольной трапеции ABCD (угол C = углу D = 90 градусам)?

Окружность проходит через вершины C и D прямоугольной трапеции ABCD (угол C = углу D = 90 градусам).

Найти радиус окружности, если известно, что окружность касается прямой AB в точке B и длины боковых сторон трапеции равны 4 и 5.

Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Докажите что прямая проведенная через середины основания трапеций проходит через точку пересечения диагоналей трапеции и точку прододжения боковых сторон?

Докажите что прямая проведенная через середины основания трапеций проходит через точку пересечения диагоналей трапеции и точку прододжения боковых сторон.

Видео:8 класс, 6 урок, ТрапецияСкачать

Внутри равнобедренной трапеции ABCD с основаниями BC = 12, AD = 28 и боковой стороной CD = 10 выбрана точко О так, что окружность с центром в точке О касается оснований трапеции и стороны CD ?

Внутри равнобедренной трапеции ABCD с основаниями BC = 12, AD = 28 и боковой стороной CD = 10 выбрана точко О так, что окружность с центром в точке О касается оснований трапеции и стороны CD .

Найдите площадь треугольника ABO.

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

ABCD — прямоугольная трапеция с прямым углом А и меньшим основанием ВС = 2?

ABCD — прямоугольная трапеция с прямым углом А и меньшим основанием ВС = 2.

Окружность с центром в точке О касается прямой ВС в точке С и проходит через точки А и D.

Найдите длину стороны АВ, если известно, что она больше радиуса этой окружности.

Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Окружность, построенная, как на диаметре, на боковой стороне AB равнобокой трапеции ABCD, касается боковой стороны CD и пересекает большее основание AD ещё в точке H?

Окружность, построенная, как на диаметре, на боковой стороне AB равнобокой трапеции ABCD, касается боковой стороны CD и пересекает большее основание AD ещё в точке H.

Найти площадь трапеции, если BC = 2 и ∠BAD = 60° .

Если вам необходимо получить ответ на вопрос Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T ?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Cos180(Sin135tg60 — Cos135) = — 1 * [Sin(90 + 45) * √3 — Cos(90 + 45)] = = — 1 * ( √3 Cos45 + Sin45) = — ( √3 * √2 / 2 + √2 / 2) = — √2 / 2( √3 + 1).

3) Треугольник АДС = СВД : 1. Угол ВАС = ДАС 2. АД = АВ 3. АС — Общая сторона. 4) Треугольник АВД = СВД : 1. ВС = АД 2. Угол СВД = АДВ 3. ВД — Общая сторона Что и требовалось доказать.

Угол между биссектрисами углов треугольника равен ∠АОВ = 90° + 0, 5∠АСВ = 90 + 45 = 135° ΔАОВ. По теореме косинусов : АВ² = ОА² + ОВ² — 2·ОА·ОВ·соs135° = 5 + 10 + 2·√5·√10·√2 / 2 = 5 см. ВС = 3 см ; Ас = С = 4 см. ПериметрΔАВС равен 12 см.

Правильный ответ — копоть. Копоть — корень, нулевое окончание. Порез не подходит, потомучто приставка по — , корень — рез — , ледокол — корень — лед — , соединительная (о) и корень — кол — . Сразу : с — префикс (приставка) раз — корень у — суффикс..

Если угол BOD и угол DOC равны то 26 + 26 = 52 Угла ABD нету может угол AOB Если угол AOB то он будет 180 — 52 = 128.

1. Припустимо, що трик. ABC і DEF рівні. 2. Відкладемо з кутів А і D медіани до точок М і М¹ відповідно. 3. Трик. АМВ дор. Трик. DM¹E за 2 орт, бо : AB = DE як відповідні сторони BM = EM¹ = 0, 5BC = 0, 5EF як половини відповідних сторін кути AB..

Ну вроде так, но это не точно.

Используйте теорему о сумме углов треугольника, а также о равных противоположных углах ромба, диагональ всегда делит угол на равные части, а значит углы АСД = САД = 35 градусов Угол АВС = 180 — (АСД + САД) = 180 — (35 + 35) = 110 градусов.

Видео:ОГЭ по математике, задание 26, тренировочный вариант 1Скачать

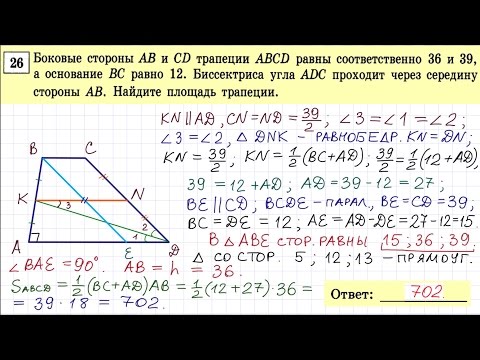
Окружность проходит через вершины большей боковой стороны прямоугольной трапеции

БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3

3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3

4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности.
б) Найдите A₁ H, если BC = 2√3.

5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10

6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4

7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6

8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.

9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.

11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88

12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.

13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.

14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .}

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65

18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4

19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .

б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2

20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3

21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1

22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36

23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4

24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.

25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.

26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.

28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.

📽️ Видео

✓ Все сюжеты по планиметрии из ЕГЭ за 50 минут | ЕГЭ. Задание 16. Профильный уровень | Борис ТрушинСкачать

Задача 6 №27834 ЕГЭ по математике. Урок 100Скачать

Планиметрия с нуля и до уровня ЕГЭ 2023 за 4 часа | Вся теория по №1,16 | Математика профильСкачать

Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать

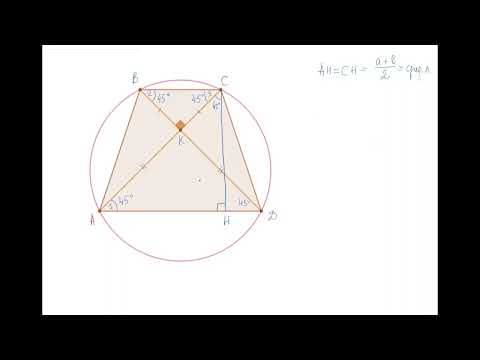
Жесткая планиметрия на систему окружностей с трапецией | ЕГЭ 2023 Профильная математикаСкачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

ОГЭ задача 25 - три подобияСкачать