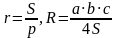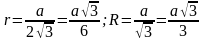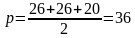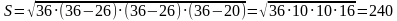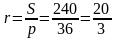Разделы: Математика
На итоговых уроках по геометрии времени на то, чтобы прорешать задачи по всему курсу в целом практически не остается. А в КИМы ЕГЭ традиционно включаются задачи, решение которых требует знаний планиметрии по теме «Вписанные и описанные окружности». Поэтому предложенный материал поможет не только вспомнить данную тему, но и систематизировать ранее полученные знания по решению планиметрических задач на вписанные и описанные окружности, а также подготовиться к решению подобных задач в ЕГЭ. При этом предполагается, что ученик хотя бы на минимальном уровне владеет всем курсом школьной геометрии (планиметрии).
Первым и важнейшим этапом решения геометрической задачи является построение чертежа. Нельзя научиться решать достаточно содержательные задачи, не выработав прочных навыков по изготовлению «хороших» чертежей, не выработав привычки (даже рефлекса) – не начинать решать задачу, пока не сделан «большой и красивый» чертеж. В качестве основного метода решения геометрических задач выдвигается алгебраический метод с составлением последующего алгоритма. Ставя во главу угла алгебраический метод, необходимо предостеречь от чрезмерного увлечения алгеброй и счетом, не забывать о том, что речь идет все же о геометрических задачах, а поэтому, работая над задачей, следует искать геометрические особенности, учиться смотреть и видеть геометрию. Выделив два слагаемых, определяющих умение решать геометрические задачи, – чертеж плюс метод, добавим сюда третье – владение определенными теоремами и опорными задачами, известными геометрическими фактами.
I. Необходимые теоремы и опорные задачи для окружности, вписанной в треугольник и четырехугольник, и окружности, описанной около треугольника и четырехугольника. (Приложение 1)
II. Решение задач по готовым чертежам (удобно воспользоваться кодоскопом).
При этом ученики устно объясняют ход решения задач, формулируют теоремы и опорные задачи, применяемые при решении задач по готовым чертежам.
Готовый чертеж
Дано
Найти
Решение
Ответ
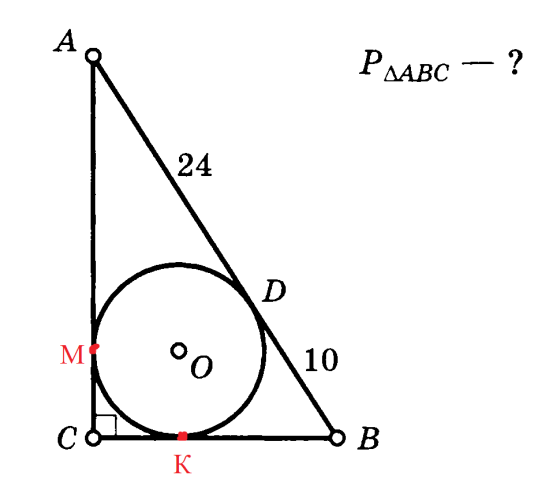
PABC = ?
AB = BC = 12
MC = CN = 7, AC = 14, AK = AN = 7,
PABC = 12 + 12 + 14 = 38
Ответ: PABC = 38
AB = 6,
АО = 
PABC = ?
1)
, 
2) АВ = ВС,
, т.к. ВО – биссектриса 3)
АВС – равносторонний, PABC = 6 • 3 = 18 Ответ: PABC = 18
АВ = 3,
ВД = 4
1. Доказать: NM
AD 2. R = ?
AN и AC DN, т.е. AC и DB – высоты АND, тогда NK – высота, т.к. они пересекаются в одной точке. Значит NM
AD. 2. AD =
= 5, R = 
Ответ: R = 2,5
АВС, R = 
= 1,5 Ответ: R = 1,5
ОК = 5
R = ?
. BKO – прямоугольный, ВК = AK = 12, КО = 5, ВО =
= 13 = R Ответ: R = 13
III. Решение задач.
1. Найти периметр прямоугольного треугольника, если радиус вписанной окружности 2 см, а гипотенуза 13 см.
 | Пусть AM = AN = x, тогда AC = x + 2, CB = 2 + 13 – x = 15 – x (x + 2) 2 + (15 – x) 2 = 169 x 2 – 13x + 30 = 0 x1 = 10, x2 = 3; AC = 6, CB = 12; P = 30 см Ответ: P = 30 см. |
2. Радиус вписанной в прямоугольный треугольник окружности 3 см, О – центр вписанной окружности, 
, 
. Найти площадь треугольника.
 | АО – биссектриса, AKO – прямоугольный, sin  = sin 30 о =  , АО = 6, AN = AK =  = 3 , AC = 3 + 3, tg 60 о =  , CB =  SABC =  =  Ответ: S = см2. |
3. Периметр треугольника 84. Точка касания вписанной окружности делит одну из сторон на отрезки 12 и 14. Найти радиус вписанной окружности и площадь АВС, если ОВ = 18, О – центр вписанной окружности.
 | P = 84, KB = BN = 16, ON =  =  = r AB = 28, BC = 30, AC = 26 По формуле Герона: SABC =  = 336 Ответ: r = ; S = 336. |
4. В равнобедренном треугольнике расстояние от центра вписанной окружности до вершины не равного угла 5 см. Большая сторона 10 см. Найти радиус вписанной окружности.
 | OB = 5,  , OM = OB .  =  , BH = 5 + r, AH = 2r, AHB – прямоугольный,  4r 2 = 100 – (5 + r) 2 , r 2 + 2r – 15 = 0, r1 = – 5, r2 = 3 Ответ: r = 3 см. |
5. Основание равнобедренного треугольника, вписанного в окружность радиуса 5 см, равно 6 см. Найти периметр треугольника.
 | AHO – прямоугольный: OH = 4, BH = 4 + 5 =9, AB = BC =  =  P =  Ответ: P = см. |
6. Периметр треугольника АВС равен 72 см. AB = BC, AB:AC = 13:10. Найти радиус описанной около треугольника окружности.
 | AB + BC + AC = 72,  ,  AC = 20, AB = BC =  = 26, BH =  = 24 BN = NA = 13,   , R =  Ответ: R =  см. |
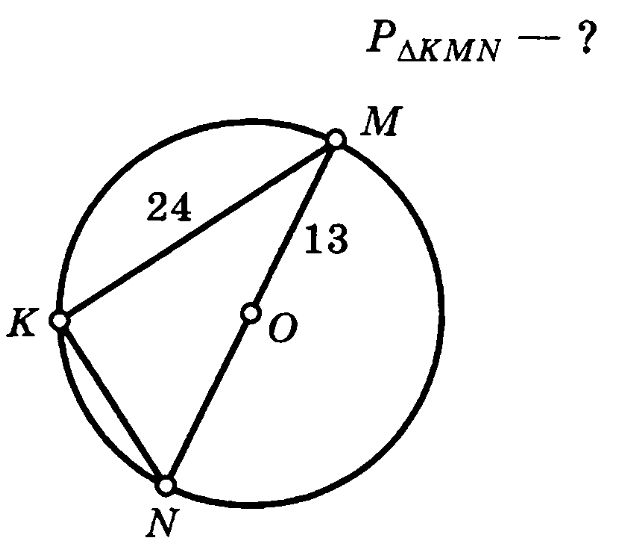
7. Основание тупоугольного равнобедренного треугольника равно 24 см, а радиус описанной окружности 13 см. Найти боковую сторону треугольника.
 | OC = 13, AC = 24, HC = 12 HOC – прямоугольный, OH =  = 5 BH = BO – OH =13 – 5 = 8 BHC – прямоугольный, BC =  Ответ:  см. |
8. Окружность, диаметром которой служит АС треугольника АВС, проходит через точку пересечения медиан этого треугольника. Найти отношение длины стороны АС к длине проведенной к ней медианы.
 | AO = OC = R = OM, BM = 2R, BO = 3R,  Ответ:  . |
9. Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
 | SABCD =  Т.к. окружность вписанная, то AB + CD = AD + BC = 20 h = 2r = 8,  , SABCD = 10 • 8 = 80 Ответ: 80. |
10. Дан ромб ABCD. Окружность, описанная около треугольника ABD, пересекает большую диагональ ромба AC в точке E. Найдите CE, если AB = 
, BD = 16.
 | AOB – прямоугольный: AO =  = 16 AD = 32 По теореме об отрезках пересекающихся хорд: BO • OD = AO • OE, 8 • 8 = 16 • OE, OE = 4, CE = 16 – 4 = 12 Ответ: 12. |
IV. Задачи для самостоятельного решения.
1. Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, а радиус описанной окружности равен 5 см. Найдите больший катет треугольника.
2. Около равнобедренного треугольника с основанием АС и углом при основании 75о описана окружность с центром О. Найдите ее радиус, если площадь треугольника ВОС равна 16.
3. Найдите радиус окружности, вписанной в остроугольный треугольник АВС, если высота BH равна 12 и известно, что 
, 
.
4. Один из катетов прямоугольного треугольника равен 15, а проекция второго катета на гипотенузу равна 16. Найдите диаметр окружности, описанной около этого треугольника.
5. В равнобедренный треугольник АВС вписана окружность. Параллельно его основанию АС проведена касательная к окружности, пересекающая боковые стороны в точках D и E. Найдите радиус окружности, если DE = 8, AC = 18.
6. Около треугольника ABC описана окружность. Медиана треугольника AM продлена до пересечения с окружностью в точке K. Найдите сторону AC, если AM= 18, MK = 8, BK = 10.
7. Окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.
8. Угол В треугольника АВС равен 60 о , радиус окружности, описанной около АВС, равен 2. Найти радиус окружности, проходящей через точки А и С и центр окружности, вписанной в АВС.
9. Стороны треугольника равны 5, 6 и 7. Найти отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.
10. Радиус окружности, вписанной в прямоугольный треугольник, равен полуразности его катетов. Найти отношение большего катета к меньшему.
Ответ: ().
11. Диагонали четырехугольника ABCD, вписанного в окружность, пересекаются в точке М, прямые AB и CD пересекаются в точке N. Известно, что 
, 
. Найти 
и 
.
12. Высоты AH и BK остроугольного треугольника ABC пересекаются в точке M, 
. Найдите градусную меру угла ABO, где O – центр окружности, описанной около треугольника ABC.
13. Около окружности описана равнобочная трапеция с основаниями 5 и 3. Найти радиус окружности.
Ответ: (
).
14. В равнобедренный АВС с основанием BC вписана окружность. Она касается стороны AB в точке M. Найдите радиус окружности, если AM = 6, BM = 24.
15. Дан прямоугольный треугольник ABC с прямым углом C. Через центр O вписанной в треугольник окружности проведен луч BO, пересекающий катет AC в точке M. Известно, что AM = 
, 
. Найдите гипотенузу и радиус окружности, описанной около треугольника.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать
Треугольники вписанная и описанная окружность задачи на готовых чертежах
Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
значит, 
Приведем другое решение.
Высота правильного треугольника равна 3 радиусам вписанной окружности, поэтому она равна 18.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Окружность, описанная вокруг трапеции, описана и вокруг треугольника 
Это треугольник равнобедренный, угол при вершине равен 120°, углы при основании равны 30°. Найдем его боковую сторону:
откуда 
Тогда по теореме синусов:
Приведем другое решение (Р. А., СПб.).
Хорды AD, DC и CB равны, поэтому равны и стягиваемые ими дуги. Вписанный угол А равен 60°, он опирается на две из этих дуг и равен половине их суммы. Поэтому каждая из дуг равна 60°, их сумма равна 180°, а хорда АВ является диаметром. Отсюда получаем, что искомый радиус равен 6.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Решение задач по теме «Вписанная и описанная окружности»
Урок №7. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.
Просмотр содержимого документа
«Решение задач по теме «Вписанная и описанная окружности»»
Тема: Решение задач по теме «Вписанная и описанная окружности»
Задачи: продолжить формирование навыков решения задач по теме.
Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.
Формулы нахождения радиуса вписанной r и описанной R около треугольника окружностей.
Для любого треугольника:
Для равностороннего треугольника.
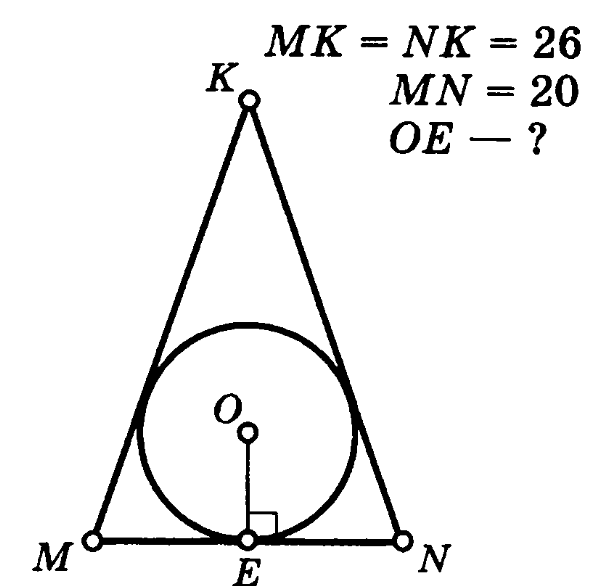
Задача 1. В равнобедренном треугольнике MKN боковые стороны равны 26, а основание – 20. В треугольник вписана окружность с радиусом ОЕ. Найти длину ОЕ.
Решение (краткое). Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле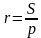 
, где р – полупериметр.
Ответ: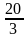 
.
Задача 2. Прямоугольный треугольник KMN описан около окружности радиуса 13. Один из катетов треугольника равен 24. Найти периметр треугольника.
Решение (краткое). MN=d=2r=26, по теореме Пифагора KN=10, Р=60.
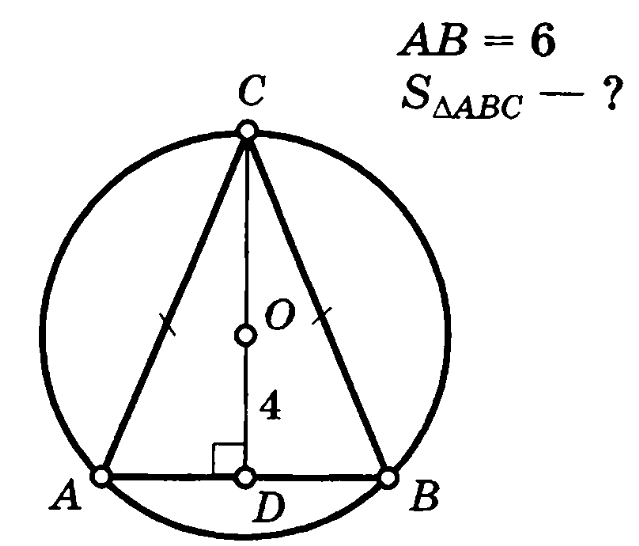
Задача 3. Равнобедренный треугольник АВС вписан в окружность, отрезок ОD=4. Найти площадь треугольника.
Решение (краткое). ОВ=5, ОС=ОВ=5, СD=9, S=0.5*9*6=27.
Задача 4. Прямоугольный треугольник описан около окружности. Точка D делит гипотенузу на две части, длинами по 10 и 24. Найти периметр треугольника.
Решение (краткое). DB=DK=10, AD=AM=24.
KOMC – квадрат, т.к. ОК перпендикулярен СВ, ОМ перпендикулярен АС и KC=CM, OK=OM=r.
Пусть KC=CM=х, тогда ВС=10+х, АС=24+х, АВ=24+10=34.
🎥 Видео
Окружность вписанная в треугольник и описанная около треугольника.Скачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
Вписанная и описанная окружности | Лайфхак для запоминанияСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Построить описанную окружность (Задача 1)Скачать
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Вписанная и описанная окружности. ЗадачиСкачать
ГОВОРЯТ, ОТВЕТ "8" НЕ НАСТОЯЩИЙ! Ограничения: 16+.Скачать
КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать
Замечательные точки треуг-ка. 8 класс.Скачать
Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать
Четырехугольники, вписанные в окружность. 9 класс.Скачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать
8 класс, 38 урок, Вписанная окружностьСкачать
Вписанная окружностьСкачать
Все о вписанных и описанных окружностях с нуля | PARTAСкачать
