Теорема пифагора для окружности (5 видео)

Универсальная формула теоремы Пифагора

В прямоугольном треугольнике сумма квадратов катетов равняется квадрату гипотенузы.
(теорема Пифагора)
2 2 2
A + B = C

Эта формула для случая, когда вершина прямого угла треугольника лежит на окружности проходящей через две другие вершины, а гипотенуза является диаметром этой окружности (Рис.2) и является частным случаем другой)(универсальной) формулы:

2 2 2 2 2
A + B + C + D = D (диаметр) Пояснено на Рис.1

Где через круг проведены две перпендикулярные прямые (хорды) и получены четыре а,в,с и d отрезка (катета) — как отрезок от окружности то точки пересечения прямых.
D — диаметр круга.

Формулировка. Если через круг провести две перпендикулярные прямые, то сумма квадратов
четырех полученных отрезков равняется квадрату диаметра.
Также. Из формулы:квадрату диаметра равна сумма квадратов противоположных хорд.
Также легко получается формула площади круга: сумма квадратов перпендикулярных отрезков умноженная на 0.785 что есть 11 деленное на 14.

И, конечно, сумма квадратов хорд (выделено синим на фиг 1) равняется квадрату диаметра.
примечание автора. В литературе такого описания не нашел.
Возможно: в древности она была известна, но забыта.

Доказательства есть. Оно достаточно простое и основано на построениях.

Содержание

Окружность — модель устройства мира
Теорема Пифагора
Основные понятия
Теорема Пифагора: доказательство
Обратная теорема Пифагора: доказательство
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?
Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?
📺 Видео

Видео:Уравнение окружности - это просто теорема ПифагораСкачать

Окружность — модель устройства мира

Число Пи ( π ) и Золотая пропорция (φ) связаны абсолютными тождествами (см. Тождественность числа Пи и Золотой пропорции):

При этом 2* π = 360° — это окружность.

Число Пи (выраженное в градусах) — угловая величина и Золотая пропорция – линейная величина, являются различными математическими выражениями одного и того же закона Мироздания, суть которого — целостность и гармоничность мира.

2) Золотая пропорция и уравнение окружности

Золотая пропорция, есть частный случай уравнения окружности x 2 + y 2 = r 2 , при r = 1, а x = y 2 , где x = y 2 – это уравнение параболы (см. Тождественность числа Пи и Золотой пропорции).

Если есть два параметра, числа или явления, связанные между собой Золотой пропорцией, то это говорит о том, что есть также уравнение окружности, включающее в себя эти параметры, т.е. всё, что гармонично, явно или неявно связано функционально через окружность.

3) Теорема Пифагора и окружность

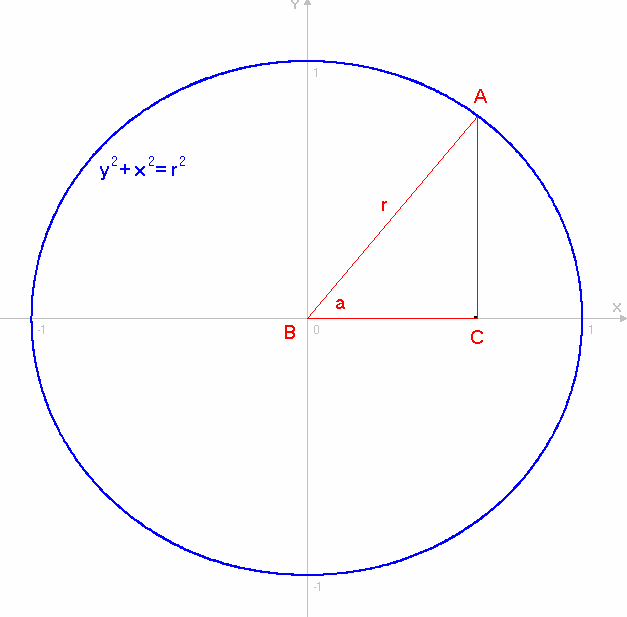
Уравнение окружности задано уравнением x 2 + y 2 = r 2 :

Рассмотрим треугольник ABC:

Т.к. величина ВС равна значению x для точки A, и величина AC равна значению y для точки A, при этом радиус окружности г равен AB, то уравнение окружности x 2 + y 2 = r 2 можно записать в виде:

(ВС) 2 + (AC) 2 = (AB) 2

А это ничто иное, как уравнение прямоугольного треугольника ABC, с катетами AC, ВС, и гипотенузой AB (Теорема Пифагора).

График взаимосвязи параметров x и y, представляет собой, множество всех точек A прямоугольного треугольника ABC, при изменяемых величинах катетов AC, ВС и постоянной величине гипотенузы AB ( r = const ).

4) Окружность и энергия

Число π в угловых единицах измерения — это 180°, и это — ровно половина окружности. Если угол, соответствующий полной окружности — 2 π , обозначить любой другой буквой, например П (П= 2 π = 360°), то уравнение площади круга запишется в виде:

а уравнение периметра окружности запишется в виде:

Сравните полученные формулы с формулой кинетической энергии тела:

и формулой импульса тела:

Не означает ли это принципиальную связь массы тела с числом Пи? Сопоставляя формулы (например, импульса и длины окружности), из размерностей величин входящих в них, можно увидеть, что отношение массы ко времени будет иметь тот же математический смысл, что и число Пи.

p = mV = ml/t, где l — длина, имеющая ту же размерность, что и радиус окружности [м], а t — время [c].

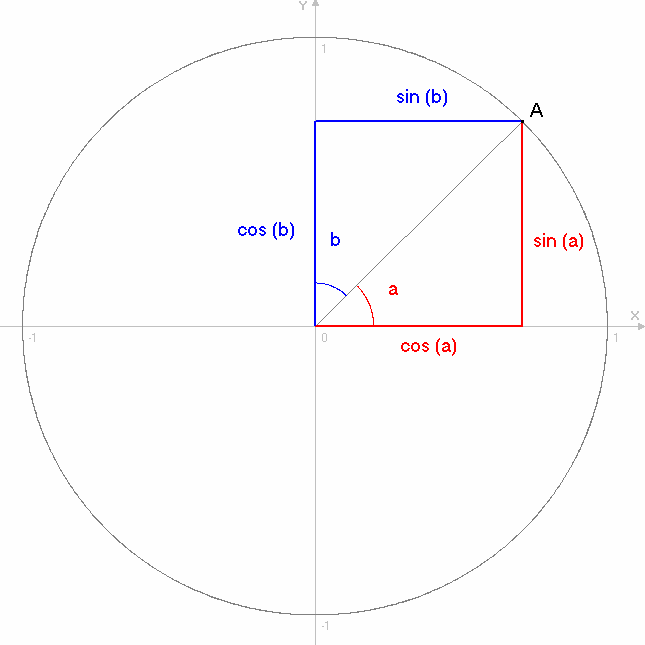
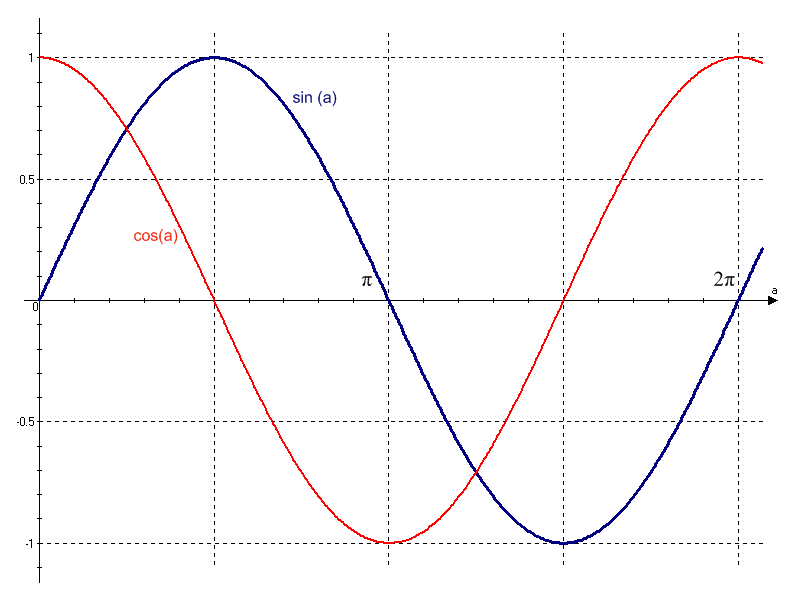
5) Синус, косинус и уравнение окружности

Так как у = sin(a), а x = cos(a), то уравнение окружности с единичным радиусом x 2 + y 2 = 1, можно записать, как:

В этом случае уравнение окружности будет отражать зависимость не от двух параметров х от y, а только от одного — угла a:

Можно перечислить всё, что, так или иначе, связано с окружностью:

Окружность — это геометрическая фигура.

Окружность — это траектория движения, орбита.

Окружность — это цикличность всех процессов происходящих в мире.

Прямая линия, это крайний случай дуги окружности с бесконечным радиусом. Так как этот случай один из бесконечного числа вариантов, и окружность с бесконечным радиусов в пределах нашей, конечной по размерам, Вселенной существовать не может, то можно утверждать, что в мире нет прямых линий, также, как и нет прямолинейного движения.

Уравнение окружности можно представить в виде уравнений синуса и косинуса, поэтому все процессы с параметрами, изменяющиемися, как функция синуса или косинуса (а это — электромагнитные излучения, свет, звук, тепловое излучение, радиоволны, рентгеновское излучение и т.д. и т.п.), т.е. все или почти все процессы во Вселенной, являются частью процессов, изменяющихся по уравнению окружности.

Уравнение, связывающее катеты и гипотенузу прямоугольного треугольника (Теорема Пифагора), есть ни что иное, как уравнение окружности в том виде, что гипотенуза — это радиус окружности, а катеты — это проекции радиуса окружности (гипотенузы) на координатные оси.

Уравнение окружности включает в себе Золотую пропорцию (как частный случай уравнения окружности), и это позволяет связать музыкальную и эстетическую гармонию, а также целостность Вселенной, с окружностью.

Косвенно, на связь с уравнением окружности указывает подобие формул кинетической энергии, импульса тела и формул площади круга и длины окружности.

Окружность в виде сферы – самая распространенная форма во Вселенной. Из всех возможных тел, при условии равенства их объёмов, только сфера имеет самую маленькую площадь поверхности.

И это конечно же, далеко не весь список.

Если человечество когда-либо найдёт универсальное математическое описание всему, что происходит в мире, то нет никаких сомнений, что этим описанием будет формула окружности.

Видео:Лекция 8. Теорема Пифагора и уравнение окружностиСкачать

Теорема Пифагора

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

a = √c 2 − b 2
b = √c 2 − a 2
c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Записывайтесь на курсы обучения математике для школьников с 1 по 11 классы!

Видео:Задача, которую боятсяСкачать