Вопрос по геометрии:
В равнобедренный треугольник АВС с основанием ВС вписана окружность. Она касается стороны АВ в точке М. Найдите радиус этой окружности, если АМ=10 и ВМ=15. Помогите пожалуйста позарез надо.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- Как написать хороший ответ?
- В равнобедренный треугольник ABC с основанием АС вписана окружность, которая касается боковой стороны BА в точке K?
- Основание AC равнобедренного треугольника ABC равно 18?
- СРОЧНО?
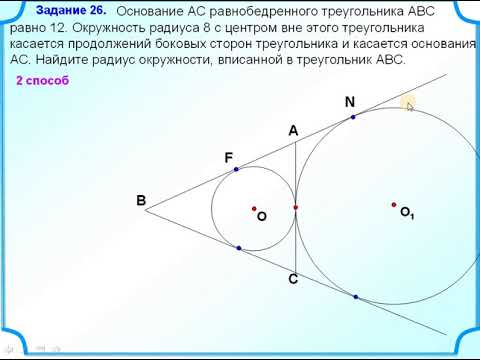
- Основание AC равнобедренного треугольника ABC равно 12?
- Расстояние между параллельными прямыми равно 6?
- Основание AC равнобедренного треугольника ABC равно 18?
- Окружность, вписанная в треугольник ABC, площадь которого равна 66, касается средней линии, параллельной стороне BC?
- Основание AC равнобедренного треугольника ABC равно 12?
- Окружность вписанная в равнобедренный треугольник ABC касается его боковых сторон AB и BC в точках M и N соответственно ?
- Основание Bc равнобедренного треугольника ABC равно 24 AB = 15?
- Боковая сторона равнобедренного треугольника равна 18, основание равно 12?
- Окружность, вписанная в треугольник. Теоремы и их рассмотрение
- Окружность, вписанная в равнобедренный треугольник
- Окружность, вписанная в прямоугольный треугольник
- Формулировка теоремы о вписанной окружности
- Теорема о центре окружности, вписанной в треугольник
- 🔥 Видео
Ответы и объяснения 1
Боковые стороны делятся точками касания на отрезки 10 и 15, а основание на два отрезка 15.
Отсюда боковые стороны равны 25, а основание 30.
Высота к основанию равна 20 (по теореме Пифагора, 20^2 + 15^2 = 25^2;)
ПОЛУпериметр равен (25 + 25 + 30)/5 = 40;
площадь 30*20/2 = 300;
ну и нужный радиус вписанной окружности равен 300/40 = 15/2;
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В равнобедренный треугольник ABC с основанием АС вписана окружность, которая касается боковой стороны BА в точке K?
Геометрия | 10 — 11 классы
В равнобедренный треугольник ABC с основанием АС вписана окружность, которая касается боковой стороны BА в точке K.
Найдите площадь треугольника ABC, если известно, что BK = 2, KА = 8.
К. треугольник равнобедренный, а АС — основание.
ВК = 2, АК = 8, тогда, АВ = 10.
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН : точка Н совпадёт с точкой касания окружности на стороне АС, т.
К. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.
Е. угол АНС = 90 градусов.
К. отрезки касательных, проведённых из одной точки, равны, т.
Е. АН = 8, тогда АС = 16.
В прямоугольном треугольнике АВН АВ = 10, АН = 8, тогда по теореме Пифагора ВН = 6.
Найдём площадь треугольника : 1 / 2 * АС * ВН = 1 / 2 * 16 * 6 = 42.
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Основание AC равнобедренного треугольника ABC равно 18?
Основание AC равнобедренного треугольника ABC равно 18.
Окружность радиуса 13 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.
Найдите радиус окружности, вписанной в треугольник ABC.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

СРОЧНО?
В равнобедренном треугольнике ABC с основанием АС и боковой стороной равное 15см, а периметром 54 см вписана окружность.
Найдите радиус окружности.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Основание AC равнобедренного треугольника ABC равно 12?
Основание AC равнобедренного треугольника ABC равно 12.
Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC.
Найдите радиус окружности, вписанной в треугольник ABC.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Расстояние между параллельными прямыми равно 6?
Расстояние между параллельными прямыми равно 6.
На одной из них лежит вершина C, на другой — основание AB равнобедренного треугольника ABC.
Известно, что AB = 16.
Найдите расстояние между центрами окружностей, одна из которых вписана в треугольник ABC, а вторая касается данных параллельных прямых и боковой стороны треугольника ABC.
Помогите пожалуйста решить задачу.
Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать
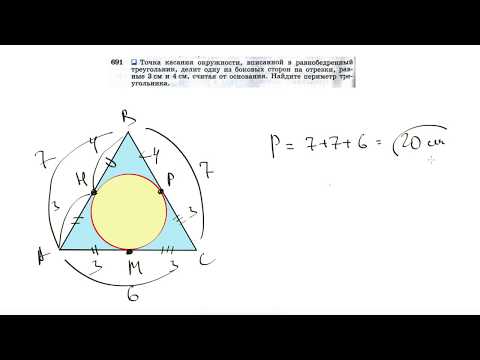
Основание AC равнобедренного треугольника ABC равно 18?
Основание AC равнобедренного треугольника ABC равно 18.
Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.
Найдите радиус окружности, вписанной в треугольник ABC.
Видео:8 класс, 38 урок, Вписанная окружностьСкачать

Окружность, вписанная в треугольник ABC, площадь которого равна 66, касается средней линии, параллельной стороне BC?
Окружность, вписанная в треугольник ABC, площадь которого равна 66, касается средней линии, параллельной стороне BC.
Известно что BC = 11.
Найдите сторону AB.
Видео:Геометрия В равнобедренный треугольник вписана окружность Точка касания делит боковую сторонуСкачать

Основание AC равнобедренного треугольника ABC равно 12?
Основание AC равнобедренного треугольника ABC равно 12.
Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.
Найдите радиус окружности, вписанной в треугольник ABC.
Видео:Геометрия В равнобедренный треугольник с углом 120 при вершине и боковой стороной а вписанаСкачать

Окружность вписанная в равнобедренный треугольник ABC касается его боковых сторон AB и BC в точках M и N соответственно ?
Окружность вписанная в равнобедренный треугольник ABC касается его боковых сторон AB и BC в точках M и N соответственно .
Докажите что MN перпендикулярна AC.
Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Основание Bc равнобедренного треугольника ABC равно 24 AB = 15?
Основание Bc равнобедренного треугольника ABC равно 24 AB = 15.
Вписанная окружность касается боковых сторон в точках E и H.
Видео:ЕГЭ Математика Задание 6#27935Скачать

Боковая сторона равнобедренного треугольника равна 18, основание равно 12?
Боковая сторона равнобедренного треугольника равна 18, основание равно 12.
Вписанная окружность касается боковых сторон в точках С и Е.
На этой странице сайта размещен вопрос В равнобедренный треугольник ABC с основанием АС вписана окружность, которая касается боковой стороны BА в точке K? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.
Видео:ОГЭ, геометрия, задачи повышенной сложности. Часть 3Скачать

Окружность, вписанная в треугольник. Теоремы и их рассмотрение
Еще в Древнем Египте появилась наука, с помощью которой можно было измерять объемы, площади и другие величины. Толчком к этому послужило строительство пирамид. Оно предполагало значительное число сложных расчетов. И кроме строительства, было важно правильно измерить землю. Отсюда и появилась наука «геометрия» от греческих слов «геос» — земля и «метрио» — измеряю.
Исследованию геометрических форм способствовало наблюдение астрономических явлений. И уже в 17-м веке до н. э. были найдены начальные способы расчета площади круга, объема шара и главнейшее открытие — теорема Пифагора.

Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:
В треугольник можно вписать только одну окружность.
При таком расположении окружность — вписанная, а треугольник — описанный около окружности.
Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:
Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Окружность, вписанная в равнобедренный треугольник
Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.
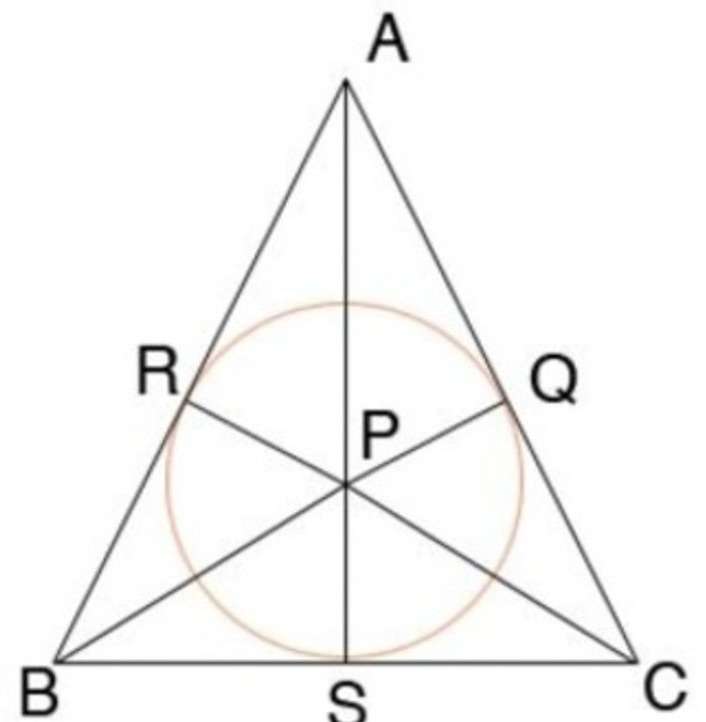
На фото ниже показана окружность, находящаяся внутри равнобедренного треугольника. Условие теоремы об окружности, вписанной в треугольник, соблюдено — она касается всех сторон треугольника AB, ВС И СА в точках R, S, Q соответственно.
Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).
Свойства теоремы об окружности, вписанной в треугольник:
- Отрезки, выходящие из одной вершины треугольника к точкам касания с окружностью, равны. На рисунке AR = AQ, BR = BS, CS = CQ.
- Радиус окружности (вписанной) — это площадь, деленная на полупериметр треугольника. Как пример, нужно начертить равнобедренный треугольник с теми же буквенными обозначениями, что на картинке, следующих размеров: основание ВС = 3 см, высота AS = 2 см, стороны АВ=ВС, соответственно, получаются по 2,5 см каждая. Проведем из каждого угла биссектрису и место их пересечения обозначим как Р. Впишем окружность с радиусом PS, длину которого нужно найти. Узнать площадь треугольника можно, умножив 1/2 основания на высоту: S = 1/2 * DC * AS = 1/2 * 3 * 2 = 3 см2. Полупериметр треугольника равен 1/2 суммы всех сторон: Р = (АВ + ВС + СА) / 2 = (2,5 + 3 + 2,5) / 2 = 4 см; PS = S/P = 3/4 = 0,75 см2, что полностью соответствует действительности, если измерить линейкой. Соответственно, верно свойство теоремы об окружности, вписанной в треугольник.
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

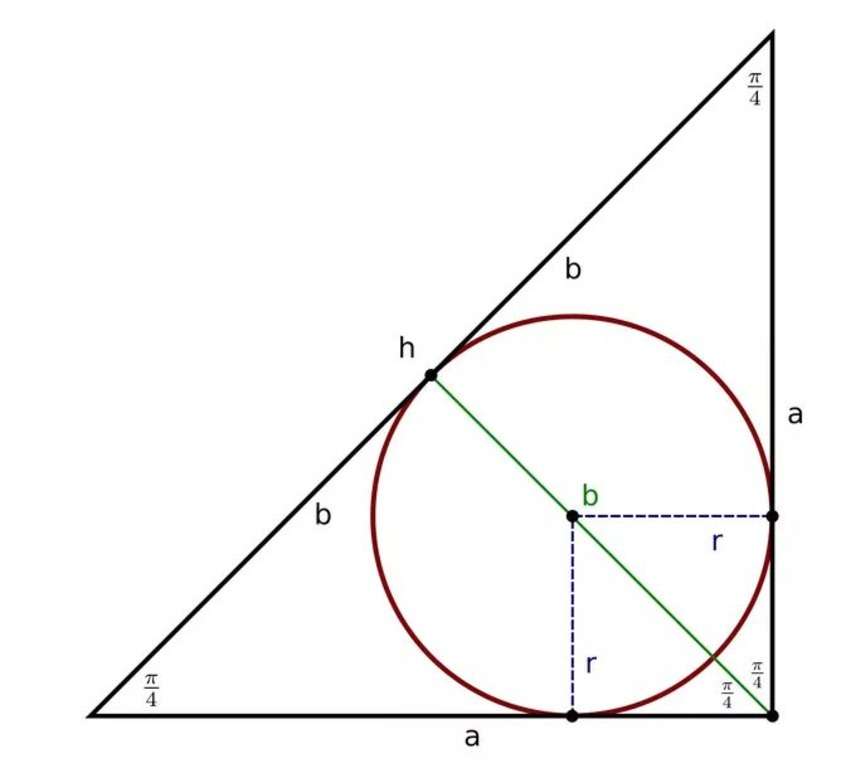
Окружность, вписанная в прямоугольный треугольник
Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.
Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.
Есть хорошая формула, которая поможет высчитать площадь треугольника — периметр умножить на радиус вписанной в этот треугольник окружности.
Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Формулировка теоремы о вписанной окружности
В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:
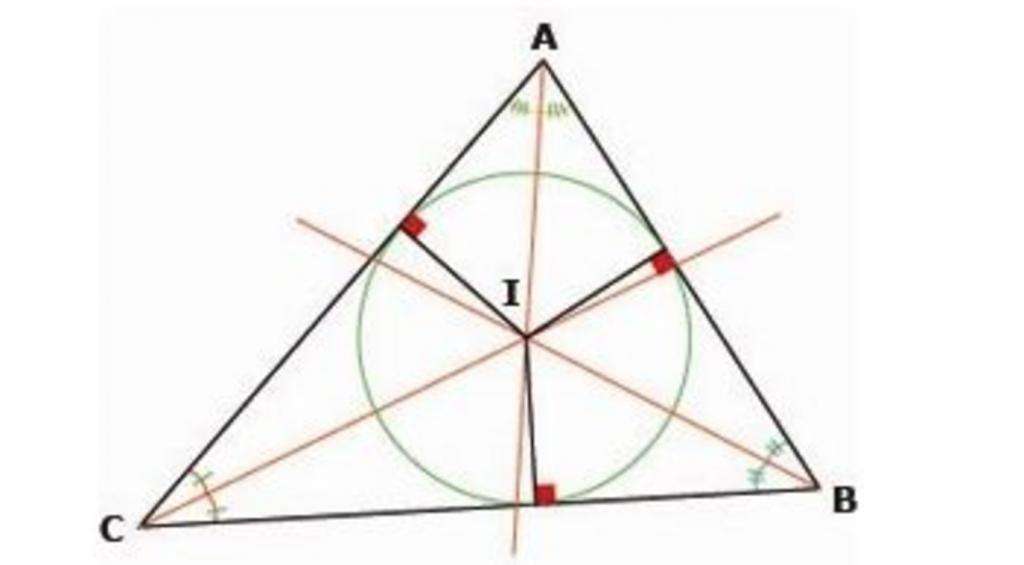
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.
На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.
Видео:Треугольник и окружность #shortsСкачать

Теорема о центре окружности, вписанной в треугольник
Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.
Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.
🔥 Видео
Геометрия К окружности, вписанной в равнобедренный треугольник с основанием 12 см и высотой 8 смСкачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать
Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать