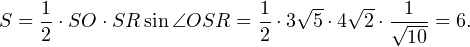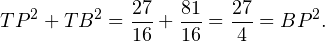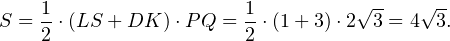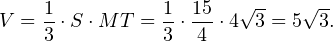Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы решим несколько задач с помощью трех аксиом и двух теорем-следствий в пирамиде.
В начале урока мы повторим аксиомы, вспомним, что такое треугольная пирамида, и повторим теоремы-следствия из аксиом. Далее мы решим несколько задач на взаимное расположение точек, прямых и плоскостей в треугольной пирамиде, опираясь на повторенный теоретический материал.
Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Билет
1. Доказать признак параллельности прямой и плоскости (на обратной стороне листа).
2. Ответить на вопросы 1-17.
3. Задачи на построение сечений 1-4.
4. Докажите, что если прямая а пересекает плоскость 

1. В основании пирамиды SABCD параллелограмм. Провести сечение через ребро AD и точку К ребра SC. Объяснить, какая фигура получилась в сечении.
2. Построить сечение AKM. Объяснить, какая фигура получилась в сечении.
3. Построить сечение, проходящее через точки M, N, K.
4. Построить сечение тетраэдра плоскостью АВС.
1. Доказать признак скрещивающихся прямых (на обратной стороне листа).
2. Ответить на вопросы 1-17.
3. Задачи на построение сечений 1-4.
4. Сторона АС 


1. Построить сечение, проходящее через точку К параллельно ребрам АВ и DC.
2. Построить сечение плоскостью NMP.
3. Построить сечение тетраэдра плоскостью АВС.
4. Построить сечение АСР, где Р – середина ребра. Объяснить, какая фигура получилась в сечении.
1. Доказать свойства параллельных плоскостей (на обратной стороне листа).
2. Ответить на вопросы 1-17.
3. Задачи на построение сечений 1-4.
4. Докажите, что отрезки, соединяющие середины противоположных ребер тетраэдра пересекаются в одной точке.
1. Построить сечение тетраэдра плоскостью NKP.
2. Построить сечение плоскостью PTN, где точки Р и Т – середины ребер AS и BS. Объяснить, какая фигура получилась в сечении.
3. Провести сечение 
4. Построить сечение плоскостью KPT.
1. Доказать признак параллельности плоскостей (на обратной стороне листа).
2. Ответить на вопросы 1-17.
3. Задачи на построение сечений 1-4.
4. Прямая b лежит в плоскости 



1. В основании пирамиды SABCD лежит параллелограмм. Провести сечение через ребро CD и точку N ребра AS. Объяснить, какая фигура получилась в сечении.
2. Построить сечение, проходящее через точки А, В, С.
3. Построить сечение АКМ. Объяснить, какая фигура получилась в сечении.
Видео:Построение проекции пирамиды. Метод прямого треугольника.Скачать

Задание 14 из ЕГЭ по математике 2016
В задании 14 ЕГЭ по математике выпускникам, сдающим экзамен, необходимо решить задачу по стереометрии. Именно поэтому научиться решать такие задачи должен каждый школьник, если он хочет получить положительную оценку на экзамене. В данной статье представлен разбор двух типов заданий 14 из ЕГЭ по математике 2016 года (профильный уровень) от репетитора по математике в Москве.
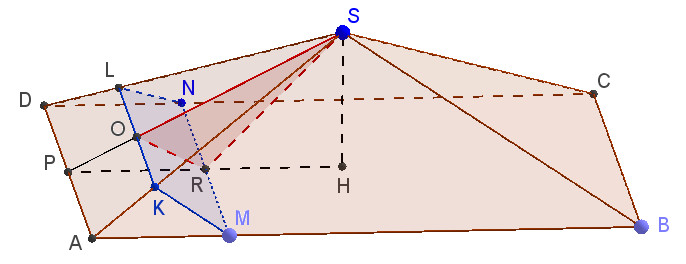
| В правильной четырехугольной пирамиде SABCD сторона основания АВ равна 16, а высота равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM = DN = 4 и АК = 3. а) Докажите, что плоскости MNK и SBC параллельны. б) Найдите расстояние от точки К до плоскости SBC. |
Доступен видеоразбор данного задания:
Рисунок к заданию будет выглядеть следующим образом:
а) Поскольку прямая MN параллельна прямой DA, которая принадлежит плоскости DAS, то прямая MN параллельна плоскости DAS. Следовательно, линия пересечения плоскости DAS и сечения KMN будет параллельна прямой MN. Пусть это линия KL. Тогда KMNL — искомое сечение.
Докажем, что плоскость сечения параллельна плоскости SBC. Прямая BC параллельна прямой MN, так как четырехугольник MNCB является прямоугольником (докажите сами). Теперь докажем подобие треугольников AKM и ASB. AC — диагональ квадрата. По теореме Пифагора для треугольника ADC находим:
AH — половина диагонали квадрата, поэтому 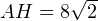
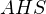
Тогда имеют место соотношения:
Получается, что стороны, образующие угол A в треугольниках AKM и ASB, пропорциональны. Следовательно, треугольники подобны. Из этого следует равенство углов, в частности, равенство углов AMK и ABS. Так как эти углы соответственные при прямых KM, SB и секущей MB, то KM параллельна SB.
Итак, мы получили, что две пересекающиеся прямые одной плоскости (KM и NM) соответственно параллельны двум пересекающимся прямым другой плоскости (SB и BC). Следовательно, плоскости MNK и SBC параллельны.
б) Поскольку плоскости параллельны, расстояние от точки K до плоскости SBC равно расстоянию от точки S до плоскости KMN. Ищем это расстояние. Из точки S опускаем перпендикуляр SP к прямой DA. Плоскость SPH пересекается с плоскостью сечения по прямой OR. Искомое расстояние есть длин перпендикуляра из точки S к прямой OR.
Действительно, KL перпендикулярна плоскости OSR, так как она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (OR и OS). Перпендикулярность OR и KL следует из теоремы о трёх перпендикулярах. Следовательно, KL перпендикулярна высоте треугольника ORS, проведенной к стороне OR. То есть эта высота перпендикулярна двум пересекающимся прямым, лежащим в плоскости KMN, а значит перпендикулярна этой плоскости.
Ищем стороны треугольника SOR. Сторону SR ищем по теореме Пифагора из прямоугольного треугольника RSH: 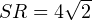
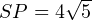
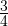
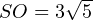
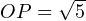
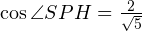
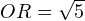
Из теоремы косинусов для треугольника SOR находим 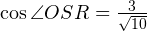
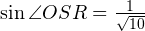
С другой стороны эта площадь равна 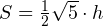
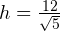
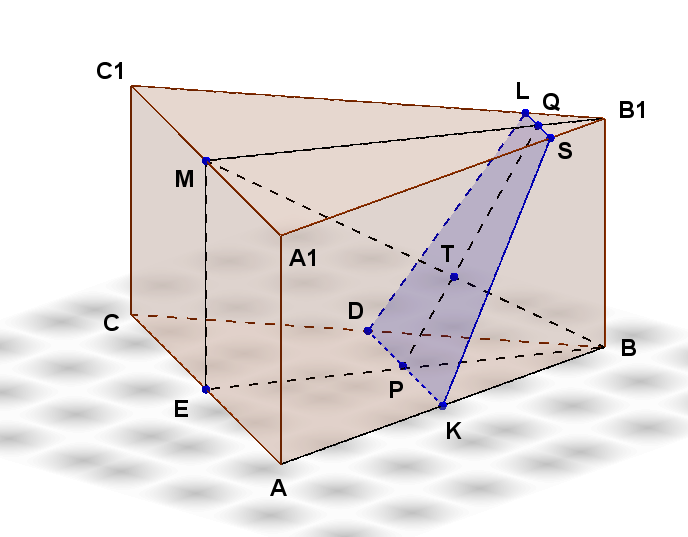
| В правильной треугольной призме АВСА1В1С1 сторона основания АВ равна 6, а боковое ребро АА1 равно 3 . На ребре В1С1 отмечена точка L так, что B1L = 1. Точки К и М – середины ребер АВ и А1С1 соответственно. Плоскость γ параллельна прямой АС и содержит точки К и L. а) Докажите, что прямая ВМ перпендикулярна плоскости γ. б) Найдите объем пирамиды, вершина которой – точка М, а основание – сечение данной призмы плоскостью γ. |
Плоскости оснований призмы параллельны, поэтому сечение будет пересекать эти плоскости по прямым LS и DK, которые также параллельны. Пусть B1M — высота треугольника A1B1C1, а BE — высота треугольника ABC. Тогда рисунок будет выглядеть следующим образом:
Из прямоугольного треугольника B1MA1 находим по теореме Пифагора 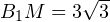
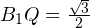
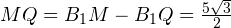
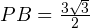
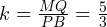
Далее из прямоугольного треугольника MBE находим 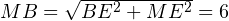
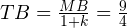
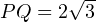
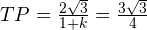
Проверяем, является ли треугольник TPB прямоугольным. Для этого используем теорему, обратную теореме Пифагора. 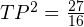
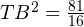
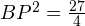
Итак, треугольник TPB прямоугольный с прямым углом T. Доказано, что 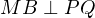
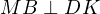
б) Сечение DLSK — трапеция, площадь которой равна:
Тогда объём искомой пирамиды равен:
Материал подготовлен репетитором по математике, Сергеем Валерьевичем
📸 Видео
Пирамида. 11 класс.Скачать

Усеченная пирамида. 11 класс.Скачать
№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

10 класс, 32 урок, ПирамидаСкачать

Построение сечений (часть 1). Пирамиды. сечениеСкачать

Лекция 5 Задача 4Скачать
ЕГЭ Задание 14 Пирамида вписана в сферуСкачать

№3. Как строить сечения пирамидСкачать

№259. В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковойСкачать

Построение сечения пирамиды по трем точкамСкачать

№55,б Пересечение пирамиды плоскостью общего положенияСкачать

Семестровая работа "Сечение пирамиды плоскостью"Скачать

Построение проекции пирамиды в трех плоскостях и построение точек 1 и 2, свободно расположенных в ееСкачать

Определение точек встречи прямой с многогранником (пирамида, призма)Скачать

Начертательная геометрия. 14 урок. Пересечение пирамиды плоскостью общего положенияСкачать

Как правильно построить сечение пирамиды плоскостью.Скачать

Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основанияСкачать

Построение усеченной пирамидыСкачать