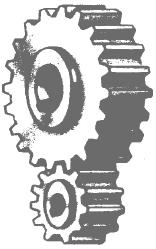
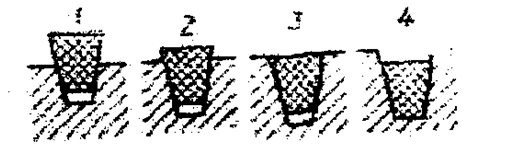
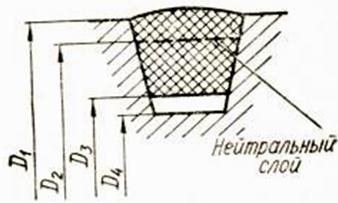
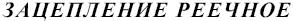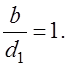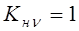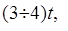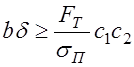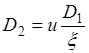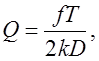- Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
- Тесты инженерной механики
- По дисциплине “Детали машин”
- Шестерня Колесо
- Шестерня Колесо
- Ременные передачи
- Модуль шестерни: виды, определение, стандартные показатели
- Что представляет собой шестерня
- Почему шестеренку называют так?
- Характеристики и применение
- Что такое модуль на чертеже?
- Как найти модуль шестерни?
- Как узнать высоту зуба шестерни?
- Как найти делительный диаметр шестерни?
- Как обозначается делительный диаметр?
- Формула расчета параметров прямозубой передачи
- Что такое модуль зубчатого колеса?
- Чему равен модуль нормального зубчатого колеса?
- Какие бывают зубчатые колеса?
- Прямозубые и косозубые колесики
- Шевронные модификации и аналоги с внутренним зацеплением
- Винтовые, круговые, секторные версии
- Конические шестерни
- Зубчатая рейка
- Звездочка
- Коронная шестерня
- В чем заключаются сходства между шестерней и зубчатым колесом
- Когда применяют цилиндрические зубчатые передачи?
- Подытожим
- 🎥 Видео
Видео:Модуль шестерни и параметры зубчатого колесаСкачать

 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
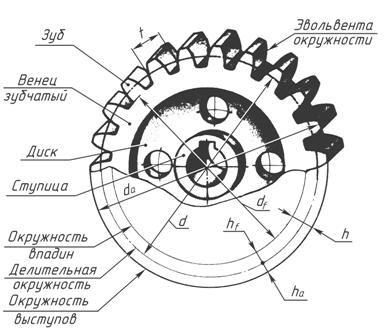
где z – число зубьев;
Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
где t – шаг зацепления.
где h a – высота головки зуба, h a = m ; h f – высота ножки зуба, h f = 1,25 m .
Диаметр окружности выступов зубьев :
Диаметр окружности впадин :
Служит для передачи вращения при параллельных осях валов.
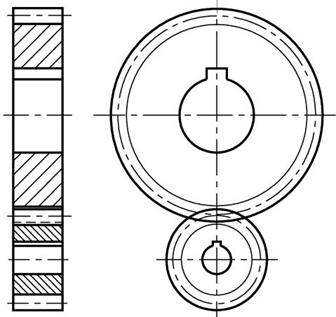
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2 .
Служит для преобразования вращательного движения в возвратно-поступательное.
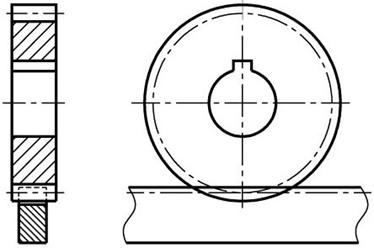
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращательного движения между валами со скрещивающимися осями.
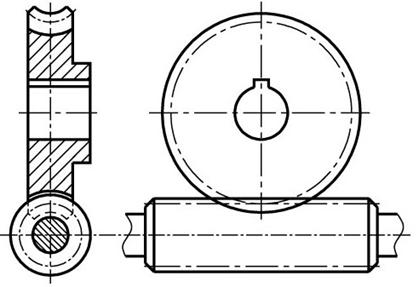
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращения при пересекающихся осях валов.
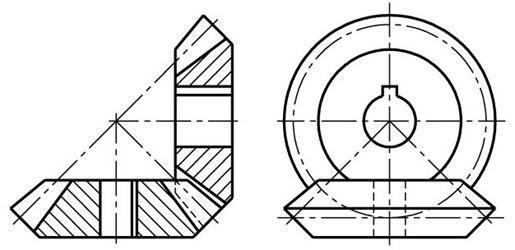
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Видео:6.3 Зубчатые цилиндрические передачиСкачать

Тесты инженерной механики
По дисциплине “Детали машин”
“Процессы, машины и оборудование агропромышленного производства”
Механические передачи
З.01. Для каких целей нельзя применить зубчатую передачу?
1. Передача вращательного движения с одного вала на другой.
2. Дискретное изменение частоты вращения одного вала по сравнению с другим.
3. Бесступенчатое изменение частоты вращения одного вала по сравнению с другим.
4. Превращение вращательного движения вала в поступательное.
З.02. Можно ли при неизменной передаваемой мощности с помощью зубчатой передачи получить больший крутящий момент?
2. Можно, уменьшая частоту вращения ведомого вала.
3. Можно, увеличивая частоту вращения ведомого вала.
4. Можно, но с частотой вращения валов это не связано.
З.03. Ниже перечислены основные передачи зубчатыми колесами:
А) цилиндрические с прямым зубом;
Б) цилиндрические с косым зубом;
В) цилиндрические с шевронным зубом;
Г) конические с прямым зубом;
Д) конические с косым зубом;
Е) конические с круговым зубом;
Ж) цилиндрическое колесо и рейка.
Сколько из них могут быть использованы для передачи вращения между пересекающимися осями?
1. Одна. 2. Две. 3. Три. 4. Четыре.
З.04. Сравнивая зубчатые передачи с другими механическими передачами, отмечают:
А) сложность изготовления и контроля зубьев;
Б) невозможность проскальзывания;
Г) малые габариты;
Д) шум при работе;
Е) большую долговечность и надежность;
Ж) возможность применения в широком диапазоне моментов, скоростей, передаточных отношений.
Сколько из перечисленных свойств можно отнести к положительным?
1. Три. 2. Четыре. 3. Пять. 4. Шесть.
З.05. Чтобы зубчатые колеса могли быть введены в зацепление, что у них должно быть одинаковым?
1. Диаметры. 2. Ширина. 3. Число зубьев. 4. Шаг.
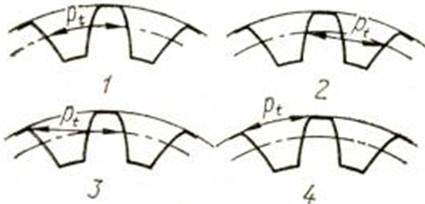
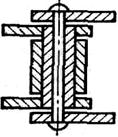
З.06. На каком рисунке правильно показан шаг зацепления (рис.1)?
З.07. Полная высота зуба в нормальном (нарезанном без смещения) зубчатом колесе равна 9 мм. Чему равен модуль?
1) 2 мм; 2) 2,5 мм; 3) 3 мм; 4) 4 мм.
З.08. Диаметр окружности выступов нормального прямозубого зубчатого колеса равен 110 мм, число зубьев — 20. Чему равен диаметр делительной окружности?
1) 110 мм; 2) 100 мм, 3) 90 мм; 4) 80 мм.
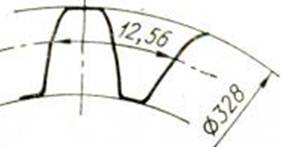
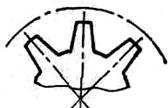
З.09. Сколько зубьев имеет это нормальное прямозубое зубчатое колесо (рис 2)?
1) 80; 2) 85; 3) 90; 4) 95.
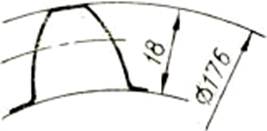
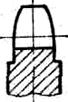
З.10. Сколько, зубьев имеет нормальное прямозубое зубчатое колесо с указанными размерами (рис. 3)?
1) 18; 2) 20; 3) 22; 4) 24.
З.11. Механизм имеет несколько последовательных передач; при вращении ведущего вала со скоростью 1000 об/мин ведомый вращается со скоростью 80 об/мин. Как правильно назвать этот механизм?
1. Коробка скоростей;
З.12. Зубчатое колесо имеет следующие характерные окружности:
1) впадин зубьев;
3) выступов зубьев;
Какая из них имеет наименьший диаметр, если у колеса 20 зубьев и модуль 5 мм?
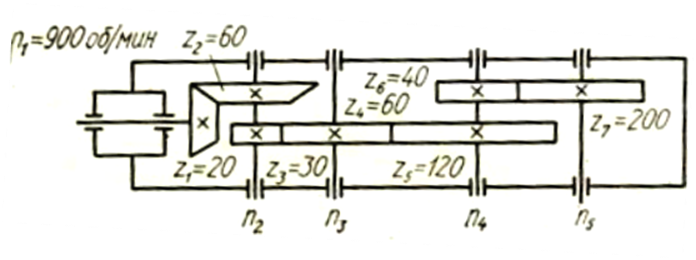
З.13. По заданным условиям определить частоту вращения на выходе П5 (рис. 4).
1) 15 об/мин; 2) 20 об/мин; 3) 30 об/мин; 4) 40 об/мин.
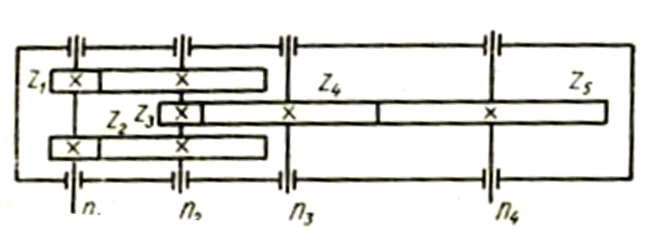
З.14. Если в редукторе указанной схемы (рис. 5) в два раза уменьшить число зубьев колеса Z4, то как изменится число оборотов в минуту на выходе N4?
1. Увеличится в четыре раза.
2. Увеличится вдвое.
4. Уменьшится вдвое.
З.15. Обычно прямозубое цилиндрическое колесо характеризуется следующими основными параметрами: Т—Модуль; D—делительный диаметр; Р—Шаг; B—Ширина венца; Z—число зубьев; 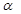
Сколько из перечисленных параметров стандартизованы?
1. Один. 2. Два. 3. Три. 4. Четыре.
З.16. Передача цилиндрическими зубчатыми колесами характеризуется следующими основными параметрами: Аω—Межосевое расстояние; И—Передаточное число; Z1, z2—числа зубьев зацепляющихся колес; ψва—коэффициент ширины зубьев.
Сколько из них должны назначаться с учетом стандартизованного ряда чисел?
1. Один. 2. Два. 3. Три. 4. Четыре.
З.17. По какому принципу построены ряды стандартных значений межосевых расстояний, передаточных чисел, коэффициента ширины зубьев?
1. Ряд целесообразных чисел.
2. Арифметическая прогрессия.
3. Геометрическая прогрессия.
4. Логарифмический ряд.
З.18. Сколько из приведенных чисел 30; 25; 20; 17; 15; 12; 10; 8 могут быть использованы для назначения числа зубьев нормального (не корригированного) зубчатого колеса?
1. Все. 2. Шесть. 3. Четыре. 4. Два.
З.19. Приведен ряд чисел для назначения передаточных чисел зубчатых передач: 1,0; 1,12; 1,25; 1,4; 1,6; 1,8; 2,0; 2,24; 2,5; 2,8; 3,15; 3,55; 4,0; 4,5; 5,0; 5,6; 6,3; 7,1; 8,0; 9,0; 10; 11,2; 12,5; 14; 16; 18; 20.
До какого номера ряда стандартизованы передаточные числа зубчатых передач?
1) 7; 2) 13; 3) 19; 4) 23.
З.20. Сколько из написанных соотношений соответствуют передаточному числу редуцирующей зубчатой передачи (индекс 1 означает ведущий элемент, индекс 2 — ведомый)?
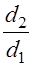
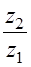
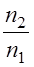
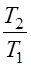
Где 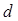
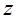
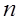
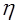
1) 1; 2) 2; 3) 3; 4) 4.
З.21. Какая из написанных зависимостей между межосевым расстоянием (А) и диаметрами зубчатых колес в редуцирующей передаче (D1, d2) неправильная (и — передаточное число)?
1) 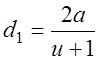
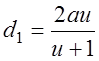
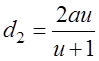
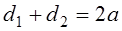
З.22. Из приведенного значения коэффициента ширины зубьев какие рекомендуются для передвижных шестерен коробок скоростей?
З.23. Отношение ширины зубчатой шестерни к ее диаметру допускают наибольшим, когда шестерня расположена:
1) на консоли вала;
2) симметрично между опорами вала;
3) несимметрично между опорами вала;
4) указанное отношение не связывают с положением шестерни на валу.
З.24. С чем связывают выбор способа получения заготовки для зубчатого колеса (точением из прутка, ковкой, штамповкой, литьем и т. п.)?
1. С шириной зубчатого венца.
3. С положением зубчатого колеса на валу.
З.25. Каким материалам для изготовления небольших зубчатых колес закрытых передач следует отдавать предпочтение?
1. Среднеуглеродистые стали обыкновенного качества без термообработки.
2. Среднеуглеродистые качественные и хромистые легированные стали нормализованные, термически улучшенные.
3. Среднеуглеродистые качественные и легированные стали с объемной закалкой.
4. Малоуглеродистые и легированные стали с поверхностной химико-термической обработкой.
З.26. В каком количестве из перечисленных случаев сочетание материалов для изготовления зубчатых колес нецелесообразно?
Видео:Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

Шестерня Колесо
СЧ 21—40 Сталь 45 нормализованная
Сталь 40Х улучшенная СЧ 21—40
Сталь 45 улучшенная Сталь 45 закаленная
Сталь 45 закаленная Сталь 45 закаленная
Сталь 40Х закаленная Сталь 20Х цементированная
Сталь 18ХГТ цементированная Сталь 40Х закаленная
Сталь 38Х2Ю азотированная Сталь 18ХГТ цементированная
Текстолит ПТК Сталь 45 закаленная
1. В двух. 2. В трех. 3. В четырех. 4. В пяти.
З.27. В зависимости от чего назначается степень точности зубчатого колеса?
1. От окружной скорости (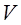
2. От частоты вращения (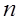
3. От передаваемой мощности (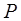
4. От нагружающего момента (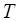
З.28. В какой из передач указанной точности следует ожидать при прочих равных условиях наибольшие динамические нагрузки?
1. Ст. 9Е; 2. Ст. 8Д; 3. Ст. 7С; 4. Ст. 6В.
З.29. Какой из приведенных возможных критериев работоспособности зубчатых передач считают наиболее вероятным для передач в редукторном (закрытом) исполнении?
1. Поломка зубьев.
2. Усталостное выкрашивание поверхностных слоев.
3. Абразивный износ.
4. Заедание зубьев.
З.30. Сравниваются два нормальных зубчатых колеса из одного материала, одинаковой ширины, с одинаковым числом зубьев и с модулем первое—2 мм; второе — 4 мм. Какая нагрузочная способность по изгибной прочности у этих колес?
2. Первого больше, чем второго.
3. Второго больше, чем первого.
4. От модуля не зависит.
З.31. Выяснилось, что при расчетах зубчатых колес на изгибную прочность ошибочно передаваемый момент был занижен в четыре раза. Чтобы передача была работоспособна, как надо увеличить модуль?
1. В четыре раза.
З.32. От чего не зависит коэффициент прочности зубьев по изгибным напряжениям (формы зуба)?
3. Коэффициента смещения исходного контура.
4. Формы выкружки у основания зуба.
З.33. С увеличением диаметра зубчатого колеса за счет большего числа зубьев при прочих равных условиях как изменится его изгибная нагрузочная способность?
1. Растет пропорционально.
2. Растет, но не пропорционально.
3. Уменьшается пропорционально.
4. Уменьшается, но не пропорционально.
З.35. Как изменится напряжение изгиба, если нагрузка на передачу увеличится в четыре раза?
2. Возрастет в два раза.
3. Возрастет в четыре раза.
4. Возрастет в 16 раз.
З.37. Сколько из перечисленных сведений о зубчатом колесе надо знать, чтобы назначить коэффициент формы зубьев по изгибным напряжениям YF? Модуль (Т); диаметр (D); число зубьев (Z); коэффициент смещения (Х); шаг (Р); угол наклона зуба (β)
1. Пять. 2. Четыре. 3. Три. 4. Два.
З.39. Как изменятся контактные напряжения, если нагрузка на зубчатую передачу возрастет в четыре раза?
2. Возрастут в два раза.
3. Возрастут в четыре раза.
4. Возрастут в 16 раз.
З.40. Какой вид разрушения зубьев наиболее характерен для закрытых, хорошо смазываемых, защищенных от загрязнений зубчатых передач?
2. Заедание зубьев.
3. Истирание зубьев.
4. Усталостное выкрашивание поверхностного слоя на рабочей поверхности зуба.
З.41. Нагрузочную способность зубчатого колеса можно повысить:
А) увеличивая модуль;
Б) улучшая материал;
В) увеличивая его ширину;
Г) увеличивая диаметр за счет увеличения числа зубьев;
Д) увеличивая угол зацепления.
Сколько из перечисленных действий повысят контактную нагрузочную способность?
1. Два. 2. Три. 3. Четыре. 4. Пять.
З.44. Коэффициенты нагрузки при расчетах цилиндрических зубчатых передач находят в основном как произведение трех коэффициентов:
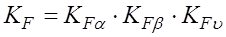
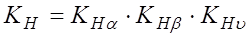
Что учитывает коэффициент Кβ?
1. Возможные кратковременные перегрузки относительно номинальной, принятой для расчета нагрузки.
2. Динамические нагрузки, связанные с неточностями изготовления зубчатых колес.
3. Концентрацию нагрузки по ширине зубчатого венца.
4. Потерю прочности зуба в связи с утонением при износе.
З.45. Явление динамичности нагрузки при расчетах цилиндрических зубчатых передач учитывают коэффициентом Кυ. С чем связывают выбор или расчет его?
1. С окружной скоростью.
2. Размещением зубчатого колеса на валу относительно опор.
3. Точностью изготовления зубчатых колес.
4. Возможностью их прирабатываемости в передаче.
Какая запись сделана ошибочно?
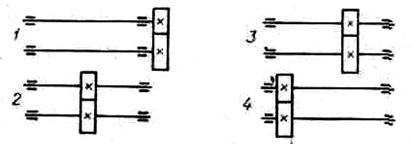
З.46. Для какой из приведенных передач следует назначить самый большой коэффициент распределения нагрузки по длине зуба (рис. 6)?
З.47. Сравниваются передачи, у которых отношение ширины зубчатого колеса (B) к диаметру (D1) составляет:
1) 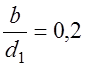
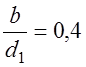
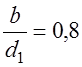
В каком случае коэффициент концентрации нагрузки будет наибольшим?
З.48. Сравниваются одинаковые зубчатые передачи, элементы которых выполнены из материалов:
Шестерня Колесо
1. Сталь 45 улучшенная Сталь 45 нормализованная
2. Сталь 45 закаленная Сталь 40 улучшенная
3. Сталь 30Х закаленная Сталь 45 закаленная
4. Сталь 40Х улучшенная Сталь 40Х улучшенная
В каком случае коэффициент концентрации будет наибольшим?
З.50. Для уменьшения динамических нагрузок в зубчатой передаче предложено:
1) сделать зуб бочкообразной формы;
2) снизить твердость колеса (HВ Mn. 4. Mt 3 м/с), какое надо ожидать значение этих коэффициентов?
1) 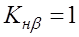
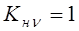
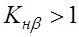
3) 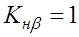
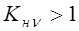
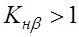
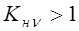
Ч.35. Какой из перечисленных факторов не влияет на коэффициент концентрации 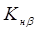
1. Диаметр колеса.
2. Диаметр червяка.
3. Число зубьев колеса.
4. Число заходов червяка.
Ч.36. Скоростной коэффициент в среднескоростной червячной передаче может быть:
1) равен единице;
2) больше единицы;
3) меньше единицы;
4) и больше, и меньше единицы в зависимости от параметров передачи.
Какая запись сделана правильно?
Ч.38. Чему равен показатель степени кривой выносливости при испытании бронз на контактную прочность (применительно к расчетам червячных передач со стальным червяком)?
1) 6; 2) 8; 3) 9; 4) 12.
Ч.39. Чему равны возможные значения коэффициента режима работы при расчетах червячных передач со стальным червяком и колесом из Бр. АЖ 9-4 на контактную прочность?
1) 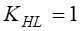
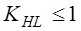
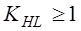
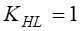
Ч.40. Червячную передачу проверяют:
1) на контактную прочность;
2) усталостную изгибную прочность;
3) прочность в условиях максимальных (пиковых) нагрузок;
Если техническими условиями на эксплуатацию допускается износ зубьев колеса до определенных пределов, в каком количестве расчетов надо учесть это обстоятельство?
1. В одном. 2. В двух. 3. В трех. 4. В четырех.
Ч.41. Допустимость износа зубьев червячного колеса до определенных пределов в некоторых расчетах учитывается введением дополнительного коэффициента нагрузки 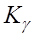
1) 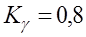
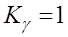
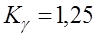
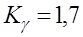
Ч.42. При обозначении:
Ft1, Ft2 —соответственно окружные силы на червяке, колесе;
Fr1, Fr2 — радиальные (распорные) силы на червяке, колесе;
Fa1, Fa2 — осевые силы на червяке, колесе. Какое равенство написано ошибочно?
1) 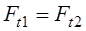
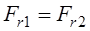
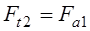
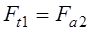
Ч.43. Из трех составляющих усилия в зацеплении (окружное, распорное, осевое), действующих на червяк, какое самое большое?
1. Окружное. 2. Осевое. 3. Распорное. 4. Все усилия равны.
Ч.44. В проверочном расчете червячной передачи на нагрев установлено, что 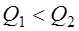
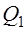
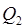
Это дает основание утверждать, что температура редуктора:
1) равна критической;
2) ниже критической;
3) выше критической;
4) ни одно из этих заключений сделать невозможно без дополнительных данных.
Ч.45. Установлено, что червячный редуктор перегревается. Для устранения этого недостатка можно:
1) оребрить корпус;
2) установить редуктор на массивную металлическую плиту;
3) обдувать редуктор вентилятором;
4) применить водяное охлаждение масла.
Какое из указанных действий наименее желательно?
Ч.46. При проектировании червячной передачи выполняются следующие расчеты:
1) определяется потребное межосевое расстояние;
2) назначаются геометрические параметры передачи;
3) проверяется контактная прочность;
4) проверяется изгибная прочность;
5) проверяется прочность в условиях максимальных (пиковых) нагрузок;
В какой последовательности они выполняются?
1) 1, 2, 6, 3, 4, 5; 2) 1, 2, 3, 4, 5, 6; 3) 2, 1, 3, 4,5,6; 4) 2, 6, 1, 3, 4, 5.
Ч.47. В задании на проектирование червячной передачи среди прочих сведений указаны:
1) момент на колесе;
2) передаточное число передачи;
3) число заходов червяка;
4) число зубьев колеса.
Без какой величины невозможно обойтись?
Ч.48. Отмечаются преимущества червячных передач с нижним горизонтальным расположением червяка по сравнению с верхним:
1) более благоприятные условия смазки;
2) более благоприятные условия теплоотдачи;
3) лучшая общая компоновка редуктора;
4) большие допускаемые окружные скорости.
Что из записанного не соответствует действительности?
Ч.49. Перечисляются стандартизованные параметры глобоидных червячных передач:
1) межосевое расстояние;
3) передаточное число;
4) число зубьев колеса и число заходов червяка.
Какой пункт записан ошибочно?
Ч.50. Из каких условий определяется потребное межосевое расстояние в глобоидных червячных передачах?
1. Из условия контактной прочности зубьев.
2. Из условия изгибной прочности зубьев.
3. Из условия износостойкости.
4. На основе обобщения экспериментальных данных о работоспособности передач.
Ц.01. К какому виду механических передач относятся цепные передачи?
1. Трением с промежуточной гибкой связью.
2. Зацеплением с промежуточной гибкой связью.
3. Трением с непосредственным касанием рабочих тел.
4. Зацеплением с непосредственным касанием рабочих тел.
Ц.02. Характеризуя цепные передачи, обычно отмечают:
1) широкий диапазон межосевых расстояний;
2) параллельность соединяемых валов;
3) отсутствие скольжения;
4) малые нагрузки на валы звездочек;
5) неравномерность вращения звездочек;
6) повышенные требования к уходу, смазке;
8) повышенная ремонтоспособность;
9) возможность передачи движения от одного вала к нескольким.
Сколько из перечисленных качеств можно считать положительными?
1) 8; 2) 7; 3) 6; 4) 5.
Ц.03. Укажите цепи, предназначенные для работы при больших скоростях.
1. Круглозвенные. 2. Грузовые. 3. Тяговые. 4. Приводные.
Ц.04. При каком взаимном расположении валов возможно применение цепной передачи?
1. Оси валов параллельны.
2. Пересекаются под некоторым углом.
3. Пересекаются под прямым углом.
4. Скрещиваются под любым углом.
Ц.05. К приводным относятся следующие цепи:
1) Круглозвенные; 2) роликовые; 3) втулочные; 4) зубчатые.
Какие из них внесены в перечень ошибочно?
Ц.06. Какая приводная цепь позволяет осуществить сравнительно плавно и бесшумно работающую передачу?
1. Роликовая. 2. Втулочная. 3. Зубчатая. 4. Все равноценны.
Ц.07. Укажите, с каким шагом приводные цепи стандартизованы? С шагом, кратным:
1) 1 мм; 2) 5мм; 3) 10 мм; 4) 25,4 мм (один дюйм).
Ц.08. Какие втулочные цепи выпускаются в настоящее время?
2. Однорядные и двухрядные.
3. Однорядные и многорядные.
4. Только многорядные.
Ц.09. Как называется цепь, представленная на рис. 11?
1. Втулочная. 2. Роликовая. 3. Зубчатая. 4. Крючковая.
Ц.10. Как называется цепь, шарнир которой в разрезе изображен на эскизе (рис. 12)?
1. Втулочная. 2. Роликовая. 3. Зубчатая. 4. Крючковая.
Ц.11. Если на чертеже приведена надпись:
«Цепь 4ПР-19,05-15000», на сколько из нижеследующих вопросов она позволяет ответить?
3. Рабочая нагрузка.
6. Нагрузка разрушения (Не меньше).
1. На шесть. 2. На пять. 3. На четыре. 4. На три.
Ц.12. Стандарт для каждой роликовой цепи устанавливает следующие размеры:
2) расстояние между внутренними пластинками;
3) ширину внутреннего звена;
4) диаметр ролика;
5) диаметр валика;
6) разрушающую нагрузку;
7) ширину внутренней пластины.
Сколько из этих характеристик непосредственно используется в расчетах на износостойкость цепи?
1. Одна. 2. Две. 3. Три. 4. Четыре.
Ц.13. Для какой цепи предназначена звездочка, изображенная на рис. 13?
1. Втулочной. 2. Роликовой. 3. Зубчатой. 4. Крючковой.
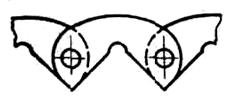
Ц.14. На рис. 14 изображено поперечное сечение венца звездочки. Для чего предназначена эта звездочка?
1. Для зубчатой цепи с боковыми направляющими пластинами.
2. Для зубчатой цепи со средними направляющими пластинами.
3. Для многорядной втулочной или роликовой цепи.
4. Для однорядной втулочной или роликовой цепи.
Ц.15. По какому из выражений рассчитывается делительный диаметр звездочки?

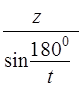
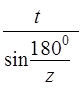
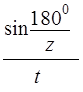
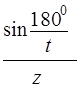
Где Z — число зубьев; T— шаг цепи.
Ц.16. Рекомендуемое наибольшее число зубьев звездочки 120—140. Какую цель преследует это ограничение?
1. Обеспечить прочность цепи.
2. Обеспечить достаточную равномерность движения цепи.
3. Ограничить выбор передаточного числа.
4. Обеспечить зацепляемость со звездочкой цепи при износе до (2—3)%.
Ц.17. Укажите интервал, в котором рекомендуется назначать наименьшее число зубьев звездочек:
1) 6-10; 2) 10-13; 3) 13-25; 4) 25-35.
Ц.18. До какой степени изношенности эксплуатируют обычно цепь?
Ц.19. По какой из приведенных формул определяют среднюю скорость движения цепи в передаче (м/с)?
1) 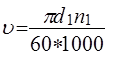
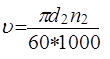
3) 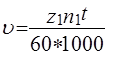
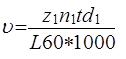
Где D1, D2—диаметры звездочек, мм; N1, N2— частота вращения звездочек, об/мин; Z1 — число зубьев ведущей звездочки; T—Шаг цепи, мм; L—Длина цепи, мм.
Ц.20. Формулы для определения передаточного числа в цепной передаче:
1) 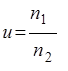
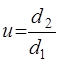
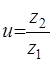
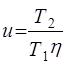
Где Z—Число зубьев; П—Частота вращения; D— Диаметр; Т—Момент; η — Коэффициент полезного действия; индекс 1 — ведущая, 2 — ведомая.
Какая из них записана неверно?
Ц.21. Какое межосевое расстояние считается оптимальным для цепной передачи?
1) 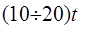
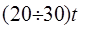
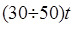
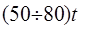
Где T — шаг цепи.
Ц.22. Какую длину цепи целесообразно назначать для цепной передачи?
2. Равную четному числу шагов.
3. Равную нечетному числу шагов.
4. Назначение длины связывают с числом зубьев звездочек.
Ц.23. Для создания целесообразного провисания ведомой ветви и возможности компенсации износа межосевое расстояние в цепных передачах делают регулируемым. Каковы целесообразные пределы регулирования?
1) 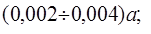
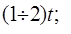
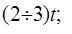
Где А — межосевое расстояние; T — шаг цепи.
Ц.24. Критериями работоспособности цепной передачи могут быть:
1) износ (удлинение) цепи;
2) усталостное разрушение пластин;
3) выкрашивание или раскалывание роликов;
4) износ зубьев звездочек.
Какой из критериев наиболее вероятный?
Ц.25. Какие материалы применяют обычно для деталей шарниров цепи (валики, втулки, вкладыши)?
1. Цементуемые стали.
2. Среднеуглеродистые стали.
3. Малоуглеродистые стали.
4. Пары сталь — бронза.
Ц.26. Какие материалы рекомендуются для звездочек?
1. Среднеуглеродистые стали без термообработки.
2. Среднеуглеродистые и легированные стали с закалкой.
4. Цветные металлы.
Ц.27. К чему приводит износ цепи?
1. К разрушению валиков.
2. К разрушению втулок.
3. К разрушению пластин.
4. К нарушению зацепления цепи со звездочками (соскакивание цепи).
Ц.28. По какому из выражений рассчитывают нагрузочную способность цепи из условия износостойкости шарнира?
1) 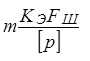
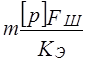
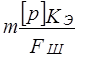
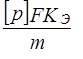
Где [р] — допускаемые удельные давления в шарнире цепи; Fш — проекция опорной поверхности шарнира; m — коэффициент рядности (для втулочных, роликовых цепей); КЭ — коэффициент эксплуатации.
Ц.29. По какой формуле рассчитывается опорная поверхность шарнира втулочных и роликовых цепей?
1) 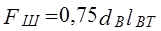
2) 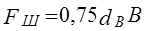
3) 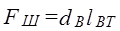
4) 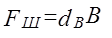
Где 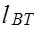
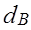
Ц.30. Назовите реальное значение коэффициента эксплуатации в формулах для расчета нагрузочной способности цепи из условия износостойкости шарнира:

Ц.31. Приведены значения коэффициента рядности в формулах для расчета нагрузочной способности многорядной роликовой цепи из условия износостойкости шарнира:
1) 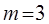
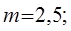
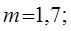
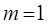
Где m — коэффициент рядности (для втулочных, роликовых цепей).
Какой из них следует принять для трехрядной цепи?
Ц.32. Упрощенно работоспособность цепи можно проверить, определяя и сравнивая с допускаемым значением запас прочности относительно разрушающего усилия. Каким выражением при этом надо воспользоваться для расчета запаса прочности?
1) 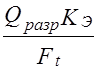
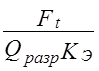
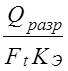
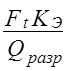
Где Qразр — разрушающее усилие; Ft — окружное усилие; Кэ — коэффициент эксплуатации.
Ц.33. В какой из перечисленных передач с промежуточной гибкой связью нагрузка на валы наименьшая?
4. Нагрузки примерно одинаковые.
Ц.34. Укажите реальные значения величины нагрузки на валы в цепной передаче:
1) 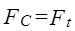
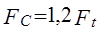
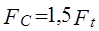
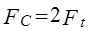
Где Ft — окружное усилие.
Видео:Лекция «Цилиндрические зубчатые передачи. Основные параметры»Скачать

Ременные передачи
РЕМ.01. Принято различать передачи:
1. зацеплением с непосредственным касанием рабочих тел;
2. зацеплением с промежуточной гибкой связью;
3. трением с непосредственным касанием рабочих тел;
4. трением с промежуточной гибкой связью.
К какому виду отнести ременную передачу?
РЕМ.02. По форме сечения ремня различают передачи:
В какой передаче часто применяют несколько параллельно работающих ремней?
РЕМ.03. Характеризуя ременную передачу, отмечают ее качества:
А) широкий диапазон межосевых расстояний;
Б) плавность, безударность работы;
В) повышенные габариты;
Г) простоту конструкции, малую стоимость;
Д) непостоянство передаточного отношения;
Е) повышенные силовые воздействия навалы и опоры;
Ж) применимость при высоких частотах вращения соединяемых валов;
З) необходимость в создании и поддерживании предварительного натяжения ремня;
И) электроизолирующую способность.
Сколько из них следует отнести к недостаткам?
1. Пять. 2. Четыре. 3. Три. 4. Два.
РЕМ.04. Приведена блок-схема привода с бесступенчатым регулированием частоты вращения в широком диапазоне
В каком соединении наиболее целесообразно применить ременную передачу?
РЕМ.05. Различают следующие виды плоскоременных передач:
Какую из них применяют для соединения параллельных валов одинакового направления вращения?
РЕМ.06. При малом межосевом расстоянии и большом передаточном числе, какую передачу предпочтительно применить?
3. Плоскоременную с натяжным роликом.
4. Плоскоременную перекрестную.
РЕМ.07. На какой ветви и как ставится натяжной ролик в ременной передаче с натяжным роликом?
1. На ведущей, оттягивая ветвь.
2. На ведущей, прижимая ветвь.
3. На ведомой, оттягивая ветвь.
4. На ведомой, прижимая ветвь.
РЕМ. 08. Какая ременная передача допускает наибольшее передаточное отношение?
4. От типа ремня передаточное отношение не зависит.
РЕМ.09. Какие ремни выпускаются промышленностью только замкнутыми (бесконечной длины)?
4. Ни один из перечисленных.
РЕМ.10. Где следует размещать ролик в ременной передаче с натяжным роликом?
1. В середине между шкивами.
2. Ближе к меньшему шкиву.
3. Ближе к большему шкиву.
4. Безразлично где.
РЕМ. 11. Стандартизованы следующие плоские ремни:
При прочих равных условиях какой ремень имеет наибольшую прочность?
РЕМ. 12. При одинаковой толщине, какой из стандартных плоских ремней позволяет осуществить передачу с минимальными диаметрами шкивов?
РЕМ. 13. Чему равен угол вклинивания клиновых ремней?
1) 40°; 2) 35°; 3) 30°; 4) 20°.
РЕМ. 14. Какой из приведенных клиновых ремней имеет наибольшее сечение?
1) 0; 2) В; 3) Б; 4) А.
РЕМ. 15. В каком сечении правильно показано положение клинового ремня в ручье шкива (рис. 15)?
РЕМ.16. Что принимается за диаметр шкива клиноременной передачи (рис. 16)?
1) 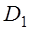
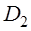
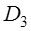
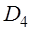
РЕМ 17. У шкивов для плоских ремней рабочая поверхность может быть:
1) с прямолинейной образующей;
4) с ломаной (реборды).
Какие шкивы не получили распространение?
РЕМ. 18. Какая характеристика плоского ремня не регламентируется стандартом?
4. Отношение толщины к диаметру меньшего шкива
РЕМ. 19. Какая из приведенных характеристик клинового ремня не регламентируется стандартом?
2. Размеры сечения.
3. Угол вклинивания.
4. Отношение толщины к диаметру меньшего шкива.
РЕМ.20. Укажите правильную рекомендацию для назначения оптимального межосевого расстояния в плоскоременных передачах:
1) 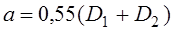
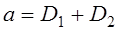
3) 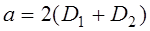
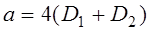
Где 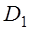
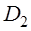
РЕМ.21. Если обозначить: 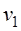
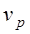
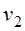
1) 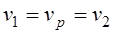
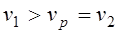
3) 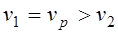
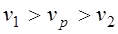
PEM.22. Каким минимальным значением ограничивают угол захвата ремнем меньшего шкива в плоскоременных передачах?
1) 90°; 2) 120°; 3) 150°; 4) 170°.
РЕМ.23. Укажите, по какой формуле определяется обычно угол охвата ремнем меньшего шкива передачи:
1) 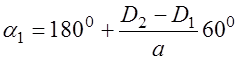
2) 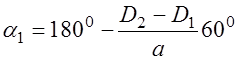
3) 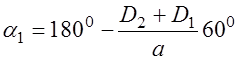
4) 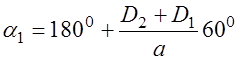
Где 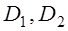
РЕМ.24. Укажите формулы, по которым с достаточной для практических расчетов точностью можно определить натяжения ведущей (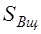
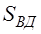
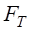
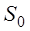
1) 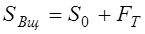
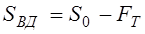
2) 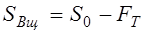
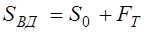
3) 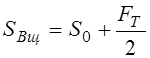
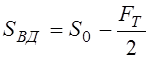
4) 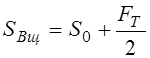
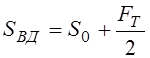
РЕМ.25. Какая цель преследуется введением ограничения на максимально возможное отношение толщины ремня к диаметру меньшего шкива?
1. Стабилизировать величину упругого скольжения.
2. Ограничить напряжения изгиба.
3. Обеспечить достаточную величину сцепления ремня со шкивом.
4. Создать определенное предварительное натяжение.
РЕМ.26. Укажите, какая формула для определения ширины ремня в плоскоременных передачах написана правильно:
1) 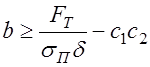
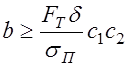
3) 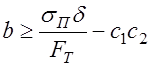
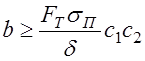
Где 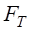
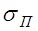
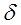
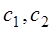
РЕМ.27. Нужное сечение ремня в плоскоременной передаче определяется по формуле:
Где 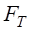
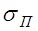
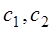
Что обеспечивают рекомендуемые в справочной литературе значения 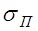
1. Максимальное использование прочностных возможностей ремня.
2. Работу передачи в оптимальных энергетических условиях (высокий КПД).
3. Максимальную долговечность ремня.
4. Максимальную износостойкость ремня.
РЕМ.28. Число ремней в клиноременной передаче определяется по формуле:
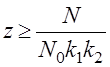
Если N —вся передаваемая мощность; 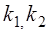
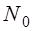
1. Единицей сечения ремня.
3. Одним ремнем при скорости 10 м/с.
4. Одним ремнем при конкретной скорости ремня в передаче.
РЕМ.29. Какая основная цель преследуется ограничением числа пробегов ремня по контуру в единицу времени?
1. Обеспечение достаточной долговечности ремня.
2. Ограничение в выборе минимального межосевого расстояния.
3. Ограничение максимальной скорости ремня.
4. Ограничение величины центробежных натяжений.
РЕМ.30. По какой из приведенных формул можно определить (приближенно) силу, действующую на валы шкивов в открытой плоскоременной передаче?
1) 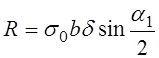
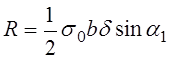
3) 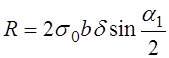
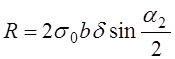
Где 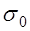
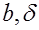
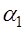
РЕМ.31. По какой формуле определяют силу, действующую на валы шкивов в клиноременной передаче?
1) 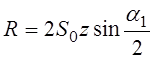
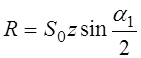
3) 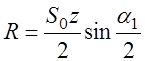
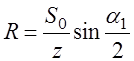
Где 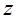
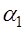
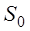
РЕМ.32. Расчет плоскоременной передачи, как правило, начинается с определения ориентировочного значения диаметра меньшего шкива по эмпирической формуле (формула М. А. Саверина ). Укажите, какая формула написана правильно.
1)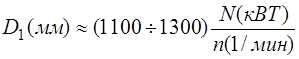
2) 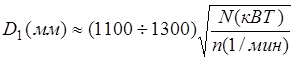
3) 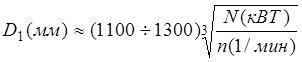
4) 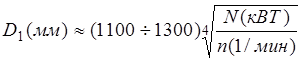
РЕМ.33. Проектирование плоскоременной передачи включает следующие расчеты:
1) определение сил, действующих на валы шкивов;
2) определение потребной ширины ремня при назначенной толщине;
3) ориентировочное определение диаметра меньшего шкива (по
эмпирической формуле М. А. Саверина);
4) назначение толщины ремня;
5) определение диаметра большего шкива:
6) назначение межосевого расстояния и расчеты длины ремня;
7) проверка угла охвата ремнем меньшего шкива;
8) проверка на число пробегов ремня по контуру в единицу времени.
В какой последовательности нужно вести расчет?
1) 1, 2, 3, 4, 5, 6, 7, 8;
2) 3, 4, 5, 6, 7, 8, 2, 1;
3) 4, 5, 6, 7, 8, 1, 2, 3;
4) 6, 3, 5, 4, 2, 1, 7, 8.
РЕМ.34. Проектирование клиноременной передачи включает следующие расчеты:
1) выбор профиля ремня;
2) назначение диаметра меньшего и расчет диаметра большего шкива:
3) назначение межосевого расстояния,
4) расчет длины ремня;
5) расчет потребного числа ремней;
6) проверка утла охвата ремнем меньшего шкива;
7) проверка на число пробегов ремня по контуру в единицу времени;
8) определение сил, действующих навалы шкивов/
В какой последовательности нужно вести расчет?
1) 1, 2, 3, 4, 5, 6, 7;
2) 2 3, 1, 4, 5, 6, 7;
3) 7, 4. 1, 3, 2. 5, 6;
4) 3, 2, 1, 5, 6, 4. 7.
РЕМ.35. Сравниваются ременные передачи с одинаковым сечением ремня:
2) нормальным клиновым;
При прочих равных условиях, в какой передаче наименьшее значение силы, действующей на валы шкивов?
Ф.01. В машиностроении приходится создавать передачи между осями:
2) пересекающимися под некоторым углом;
3) пересекающимися под прямым углом;
В каком случае применение фрикционных передач практически невозможно?
Ф.02. Укажите передаточные механизмы, в которых фрикционные передачи получила наибольшее распространение.
4. Коробки скоростей.
Ф. ОЗ. Из отмеченных недостатков фрикционных передач:
1) большие нагрузки на валы и подшипники;
2) необходимость в специальных прижимных устройствах;
3) равномерность вращения;
4) передаточное число И=var,
Какой записан ошибочно?
Ф.04. Укажите формулу, по которой определяется диаметр ведомого катка в редуцирующей фрикционной передаче.
1) 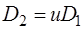
3) 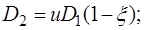
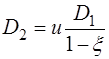
Где 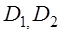
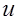
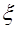
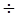
Ф.05. Если один из катков фрикционной передачи обтянуть кожей, то;
1) увеличится коэффициент трения;
2) увеличится коэффициент, учитывающий скольжение;
3) понизятся требования к точности изготовления элементов передачи;
4) должна быть снижена сила, прижимающая катки.
В каком пункте допущена ошибка?
Ф.06. По какой формуле может быть определено передаточное отношение фрикционной передачи коническими катками (угол пересечения осей 90°)?
1) 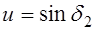
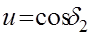
3) 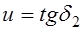
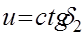
Где 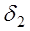
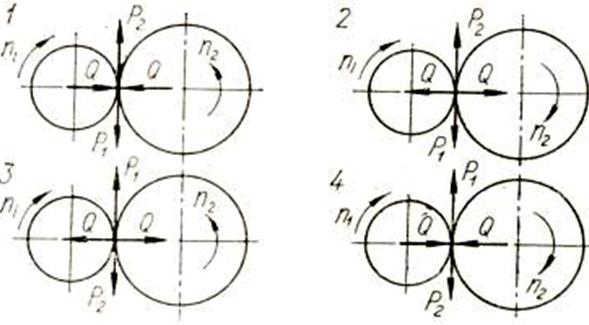
Ф.07. Укажите правильную схему действия сил на катки во фрикционной передаче (рис 17).
Ф.08. Для работы фрикционной передачи необходима сила, прижимающая катки друг к другу. Какова величина этой силы по отношению к полезному окружному усилию?
2. Может быть и больше и меньше.
3. Всегда меньше.
4. Всегда больше.
Ф.09. По какой формуле определяется потребное усилие прижатия катков во фрикционной передаче между параллельными валами?
1) 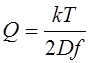
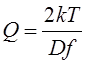
3) 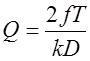
Где 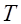
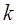
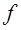
Ф.10. Во фрикционной передаче коническими катками между пересекающимися осями. внешнюю прижимающую катки силу как следует прикладывать?
1. Вдоль осей катков.
2. Перпендикулярно осям катков.
3. Вдоль линии соприкосновения катков.
4. Перпендикулярно линии соприкосновения катков.
Ф.11. В основу расчета фрикционных передач с линейным контактом (рис. 18) положена формула:
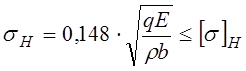
Что принимается за силу 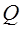
1) 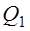
2) 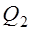
3) 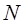
4) Окружное усилие на среднем диаметре.
Ф.13. Применительно к фрикционным передачам цилиндрическими катками между параллельными валами предложена формула
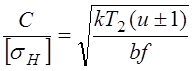
Где 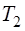
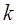
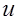
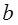
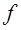
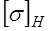
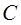
Какой параметр по ней определяется?
1. Межосевое расстояние.
2. Диаметр ведущего катка.
3. Диаметр ведомого катка.
4. Ни один из перечисленных выше параметров.
Ф.14. Расчеты показали, что во фрикционной передаче с точечным контактом рабочих теп допускаемые контактные напряжения могут быть увеличены вдвое. Во сколько раз увеличится нагрузочная способность передачи?
1) 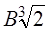
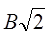
Ф.15. Ниже перечислены фрикционные вариаторы, получившие широкое промышленное распространение:
3) торовый (Святозарова);
Какой из них следует применить для создания передачи между пересекающимися осями?
Видео:Как определить шестернюСкачать

Модуль шестерни: виды, определение, стандартные показатели
Видео:Конструирование прямозубых шестернейСкачать

Что представляет собой шестерня
Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.
Шестеренчатые передачи также имеют свою классификацию:
- Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
- Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
- Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
- Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.
Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.
При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.
Почему шестеренку называют так?
Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».
Видео:формулы по расчоту прямозубых шестернейСкачать

Характеристики и применение
Зубья шестеренки находятся в радиальных плоскостях. Линия контакта прямозубых цилиндрических шестерней параллельна оси вращения.
В зависимости от необходимых нагрузочных характеристик и точности передаваемого вращения, подбирается модуль (расстояние между центрами зубов) от 1 до 6.
Используется в подвижных частях механизмов соместно с зубчатой рейкой.
Цилиндрическая зубчатая передача применяется во всех типах автоматических ворот, конвейерных линиях с повышенной нагрузкой, 3D принтерах, станках ЧПУ и многом другом.
Параметры модуля шестерни
Рассматриваемая характеристика обозначается литерой m, указывает на прочность зубчатых передач. Единица измеряется в миллиметрах (чем выше нагрузка на передачу, тем больше модульное значение). В расчете параметра используются следующие показатели:
- диаметр делительной окружности;
- шаг и число зубьев;
- эвольвент (диаметр основной окружности);
- аналогичная характеристика впадин темной шестеренки;
- высота зуба темного и светлого колеса.
В машиностроительной отрасли расчеты ведутся по стандартным значениям для удобства изготовления и замены шестерен с числами от 1-го до 50-ти.
Что такое модуль на чертеже?
Модуль — это унифицированный элемент любых систем, состоящий из взаимозаменяемого комплекса деталей массового производства. Чертеж модуля выполняется на основании ГОСТ 2.109-73 — единая система конструкторской документации (ЕСКД).
Видео:Выбираем степень точности шестерен и зубчатых колес.Обозначение на чертеже. ГОСТ 1643-81Скачать
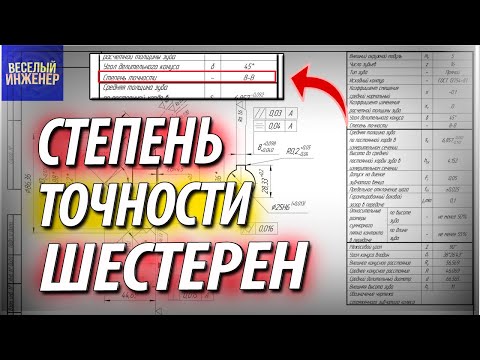
Как найти модуль шестерни?
Как определить модуль косозубой шестерни.
- Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
Видео:Как сделать партию шестерен разными способами - homemade gearСкачать

Как узнать высоту зуба шестерни?
h = ha + hf, где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
Видео:Геометрические параметры зубчатых колёс. Перекрытие. Смещение.Скачать

Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как обозначается делительный диаметр?
Окружность, являющаяся начальной при зацеплении с рейкой – делительная; её диаметр обозначается d (рис. 2). Для колес без смещения делительные окружности совпадают с начальными. Толщина зуба по делительной окружности S равна ширине впадины между двумя зубьями е.
Видео:Форма зубьев колеса в зависимости от коэффициента смещенияСкачать

Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
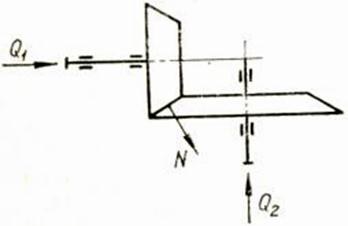
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Видео:Виды зубчатых колес. Характеристика и классификация шестеренСкачать

Что такое модуль зубчатого колеса?
m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб.
Видео:6.4 Зубчатые конические передачиСкачать

Чему равен модуль нормального зубчатого колеса?
Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.
Видео:Лекция 4. Конические зубчатые передачиСкачать

Какие бывают зубчатые колеса?
Виды зубчатых колес, шестерен
- Поперечный профиль зуба Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. …
- Продольная линия зуба Прямозубые шестерни …
- Шестерни с внутренним зацеплением …
- Винтовые шестерни …
- Секторные шестерни …
- Шестерни с круговыми зубьями
Прямозубые и косозубые колесики
Модуль и диаметр шестерни прямозубого типа — один из самых востребованных видов. Зубцы размещаются в радиальных плоскостях, а площадь контакта пары колес параллельна оси вращения. Аналогичным образом располагаются оси обеих шестерен.
Косозубые колесики представляют собой усовершенствованную вариацию вышеуказанной модификации. Зубцы находятся под определенным углом к вращательной оси. Зацепление осуществляется плавней и тише, что позволяет эксплуатировать элементы в малошумных приспособлениях, гарантируя передачу большего крутящего момента на высокой скорости. К минусам относят увеличенную площадь контакта зубцов, провоцирующую повышенное трение и нагрев деталей. Это чревато ослаблением мощности и повышенным расходом смазки. Кроме того, механическое воздействие вдоль оси шестерни требует использования упорных подшипников для монтажа вала.
Шевронные модификации и аналоги с внутренним зацеплением
Шевронные шестерни позволяют справиться с проблемами механической осевой силы. В отличие от прямых и косозубых версий, зубья выполнены в виде литеры V. Осевое воздействие двух половин приспособления компенсируется взаимодействием, что дает возможность избежать применения упорных подшипников на валу. Указанная модель самостоятельно устанавливается по оси, один из рабочих редукторов монтируется на цилиндрических укороченных подшипниках (плавающие опоры).
Модуль шестерни с внутренним зацеплением оснащается зубцами, имеющими нарезку внутри. Эксплуатация детали предполагает односторонние обороты ведущего и ведомого колеса. В такой конструкции меньше затрат уходит на трение, что способствует повышению КПД. Подобные приспособления применяются в механизмах, ограниченных по габаритным размерам, а также планетарных передачах, специальных насосах и танковых башенках.
Винтовые, круговые, секторные версии
Модуль шестерни винтового типа представляет собой цилиндр с зубцами, которые размещены по винтовому направлению. Подобные элементы устанавливаются на непересекающиеся валы, расположенные перпендикулярно по отношению друг к другу. Угол совмещения составляет 90 градусов.
Секторное зубчатое колесо — часть любой шестерни, применяемая в передачах, где не нужно вращение основного элемента на полный оборот. Такая деталь дает возможность сэкономить ценное пространство в размерах полноценного аналога.
Шестерни по модулю и количеству зубьев с круговым расположением отличаются контактным соприкосновением в одной точке зацепления, расположенной параллельно основным осям. Второе название механизма — передача Новикова. Она обеспечивает хорошие ходовые характеристики, плавную и бесшумную работу, повышенную зацепляющую способность. При этом коэффициент полезного действия таких деталей немного ниже аналогов, а процесс изготовления существенно сложнее. Указанные детали имеют значительно ограниченную отрасль эксплуатации ввиду своих особенностей.
Конические шестерни
Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.
Зубчатая рейка
Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Звездочка
Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.
Коронная шестерня
Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.
Видео:5 причин, почему механические тормоза лучше чем гидравлическиеСкачать

В чем заключаются сходства между шестерней и зубчатым колесом
Между шестерней и зубчатым колесом можно отметить несколько схожих моментов:
- Как и шестерня, зубчатое колесо может быть как ведомым, так и ведущим элементом в общей системе.
- У шестерни и у зубчатого колеса форма может быть как цилиндрической, так и конической, все зависит от той функции, которую конкретная деталь выполняет.
- При помощи шестеренки и зубчатого колеса можно маневрировать на почве скорости вращательного элемента, либо уменьшая ее, либо увеличивая.
- Шестеренки и зубчатые колеса одинаково эффективно можно использовать на электрических и бензоинструментах, однако больше всего используют именно шестеренки, так как они обеспечивают устойчивость механизма.
- Шестеренка и зубчатое колесо могут использоваться для запуска вращательных осей.
Внешние сходства между шестеренкой и зубчатым колесом обоснованы также еще тем, что зачастую эти два элемента могут выполнять схожие функции и быть взаимозаменяемыми в определенных системах и механизмах.
Видео:Детали машин. Лекция 2.3. Основы расчета зубчатых передачСкачать
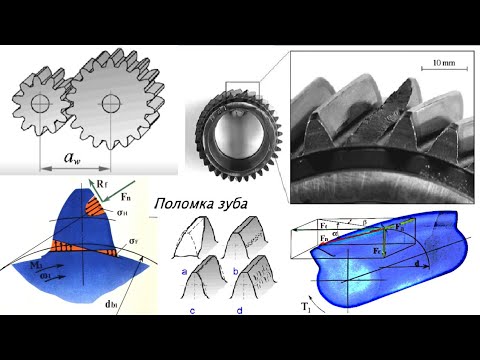
Когда применяют цилиндрические зубчатые передачи?
Цилиндрической зубчатой передачей называется передача с параллельными осями. Косозубые передачи применяют при окружных скоростях м/с; шевронные передачи – преимущественно в тяжело нагруженных передачах. … Кинематика и геометрия цилиндрические зубчатых колес.
Видео:Зубчатые передачиСкачать

Подытожим
Расчетные чертежи и схемы для шестеренок различных конфигураций преимущественно совпадают для косых и прямозубчатых версий. Основные различия возникают при расчетах на прочность. В графических отображениях применяются характеристики, ориентированные на типовые габаритные размеры шестеренок. Среди представленного ассортимента на рынке вполне реально подобрать зубчатое колесо с необходимыми характеристиками и прочностными показателями.
🎥 Видео
Чертёж прокатных роликом своими мозгами.Скачать

Что такое DIA диска? И как найти его размер!Скачать

Как делают зубчатые колеса ➤ Читаем чертеж цилиндрической шестерниСкачать

 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.