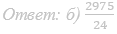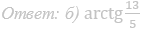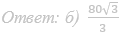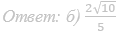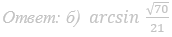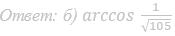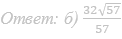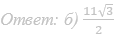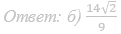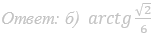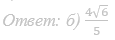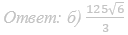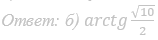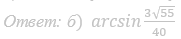Пирамида sabcd пересечена плоскостью klnm параллельной основанию как расположены прямые ad и bc

БАЗА ЗАДАНИЙ

Задание № 13. Стереометрия с доказательством.

25. Дана четырёхугольная пирамида SABCD с прямоугольником ABCD в основании. Сторона AB равна 4, а BC равна 4√2. Высота пирамиды проектируется в центр пересечения диагоналей прямоугольника. Из вершины A и C на ребро SB опущены перпендикуляры AP и CQ.
а) Докажите, что точка P является серединой отрезка BQ.
б) Найдите угол между плоскостями SBA и SBC, если ребро SD = 8.

26. Дана пирамида PABCD, в основании — трапеция ABCD с большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K.
а) Доказать, что плоскость PAB перпендикулярна плоскости PCD.
б) Найдите объём PKBC, если AB = BC = CD = 2, а высота равна 12.
Ответ: б) 4

27. SABCD — правильная пирамида с вершиной S. Точка M расположена на SD так, что SM : SD = 2 : 3. P — середина ребра AD, а Q середина ребра BC.
а) Доказать, что сечение пирамиды плоскостью MQP — равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость MQP разбивает пирамиду.
Ответ: б) 2/7

28. В треугольной пирамиде SABC известны боковые рёбра SA=SB=7, SC=5. Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите объём пирамиды SABC.
Ответ: б) 16√6

29. На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM:BM = CN:NB = 1:2. Точки P и Q — середины сторон DA и DC соответственно.
а) Докажите, что P, Q, M и N лежат в плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
Ответ: б) 13/23

30. В основании прямой треугольной призмы ABCA₁B₁C₁ лежит прямоугольный треугольник ABC с прямым углом C, AC = 4, BC = 16, AA₁=4√2. Точка Q — середина ребра A ₁ B ₁ , а точка P делит ребро B ₁ C ₁ в отношении 1 : 2, считая от вершины C ₁ . Плоскость APQ пересекает ребро CC ₁ в точке M.
а) Докажите, что точка M является серединой ребра CC ₁ .
б) Найдите расстояние от точки A ₁ до плоскости APQ.

32. В правильной треугольной призме ABCA₁B₁C₁ сторона AB основания равна 12, а высота призмы равна 2. На рёбрах B₁C₁ и AB отмечены точки P и Q соответственно, причём PC ₁ =3, а AQ = 4. Плоскость A ₁ PQ пересекает ребро BC в точке M.
а) Докажите, что точка M является серединой ребра BC.
б) Найдите расстояние от точки B до плоскости A ₁ PQ.

33. В правильной четырёхугольной пирамиде SABCD сторона AB основания равна 2√3, а высота SH пирамиды равна 3. Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды NSCD с вершиной N и основанием SCD.
а) Докажите, что точка T является серединой SM.
б) Найдите расстояние между NT и SC.
Ответ: б) √15/5

34. Дан прямой круговой конус с вершиной M. Осевое сечение конуса — треугольник с углом 120◦ при вершине M. Образующая конуса равна 2√3. Через точку M проведено сечение конуса, перпендикулярное одной из образующих.
а) Докажите, что получившийся в сечении треугольник тупоугольный.
б) Найдите площадь сечения.
Ответ: б) 4√2

35. Основанием прямой четырехугольной призмы ABCDA ₁ B ₁ C ₁ D ₁ является квадрат ABCD со стороной 5√2, высота призмы равна 2√14. Точка K — середина ребра BB ₁ . Через точки K и C ₁ проведена плоскость α, параллельная прямой BD ₁ .
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
Ответ: б) 26

36. Дана правильная пирамида SABCD. Точка M находится на SD так, что MS:SD=2:3. Точка P середина AD. Точка Q середина BC.
а) Доказать, что сечение пирамиды плоскостью MQP – равнобедренная трапеция.
б) Найдите соотношение объемов.
Ответ: б) 2/7

37. Основание прямой треугольной призмы ABCA ₁ B ₁ C ₁ является прямоугольный треугольник ABC с прямым углом C. Диагонали граней AA ₁ B ₁ B и BB ₁ C ₁ C равны 15 и 9 соответственно, AB=13.
а) Докажите, что треугольник A ₁ C ₁ B – прямоугольный.
б) Найти объем пирамиды AA ₁ C ₁ B.
Ответ: б) 20√14

Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

38. Основанием прямой треугольной призмы ABCA ₁ B ₁ C ₁ является прямоугольный треугольник ABC с прямым углом C. Грань ACC ₁ A ₁ является квадратом.
а) Докажите, что прямые CA ₁ и AB ₁ перпендикулярны.
б) Найдите расстояние между прямыми CA ₁ и AB ₁ , если AC = 4, BC = 7.

39. В правильной треугольной призме ABCA₁B₁C₁ сторона основания АВ=6, а боковое ребро AA ₁ =3. На ребре B ₁ C ₁ отмечена точка L так, что B ₁ L=1. Точки К и М – середины ребер АВ и A ₁ C ₁ соответственно. Плоскость ƴ параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости ƴ
б) Найдите объем пирамиды, вершина которой – точка М, а основание – сечение данной призмы плоскостью ƴ.
Ответ: б) 5√3

40. В правильной четырехугольной призме KLMNK ₁ L ₁ M ₁ N ₁ точка E делит боковое ребро KK ₁ в отношении KE:EK ₁ =1:3. Через точки L и E проведена плоскость α параллельная прямой KM и пересекающая ребро NN ₁ в точке F.
а) Докажите, что плоскость α делит ребро NN ₁ пополам.
б) Найдите угол между плоскостью α и плоскостью грани KLMN, если известно, что KL = 6, KK ₁ =4.

43. Длина диагонали куба ABCDA₁B₁C₁D₁ равна 3. На луче A₁C отмечена точка P так, что A ₁ P=4.
а) Докажите, что PBDC ₁ — правильный тетраэдр.
б) Найдите длину отрезка AP.
Ответ: б) √11

44. В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB=BC=AC=5√2.
а) Докажите, что эта пирамида правильная.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA=DN:NC=2:3. Найдите площадь сечения MNB.
Ответ: б) 3√6

45. В основании правильной треугольной пирамиды ABCD лежит треугольник ABC со стороной, равной 6. Боковое ребро пирамиды равно 5. На ребре AD отмечена точка T так, что AT:TD=2:1. Через точку Т параллельно прямым AC и BD проведена плоскость.
а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.
б) Найдите площадь сечения.
Ответ: б) 20/3

46. Дан цилиндр, в котором проведены диаметры оснований. AB – диаметр верхнего основания, CD — диаметр нижнего, причем отрезки AB и CD не лежат на параллельных прямых.
а) Докажите, что у пирамиды ABCD противоположные ребра равны.
б) Найдите высоту цилиндра, если AC=7, AD=6, а радиус основания цилиндра равен 2,5.
Ответ: б) √30

47. SABCD — правильная пирамида с вершиной S. Из точки В опущен перпендикуляр BH на плоскость SAD.
а) Доказать, что угол AHC=90°.
б) Найдите объем пирамиды, если HA=1 и HC=7.

48. В кубе ABCDA ₁ B ₁ C ₁ D ₁ все рёбра равны 3. На его ребре BB ₁ отмечена точка K так, что KB=2. Через точки K и C ₁ проведена плоскость α, параллельная прямой BD ₁ .
а) Докажите, что плоскость α проходит через середину ребра A ₁ B ₁
. б) Найдите угол наклона плоскости α к плоскости грани BB ₁ C ₁ C.

Задание №14. Стереометрия (на доказательство)

Дидактический материал в помощь учителю по математике для подготовки учащихся 11 классов к ЕГЭ 2020

Просмотр содержимого документа
«Задание №14. Стереометрия (на доказательство)»

Задание № 14. Стереометрия (на доказательство).

2. В кубе ABCDA₁B₁C₁D₁ все рёбра равны 5. На его ребре BB₁ отмечена точка K так, что KB=4. Через точки K и C₁ проведена плоскость α, параллельная прямой BD₁.
а) Докажите, что A₁P:PB₁=3:1, где P — точка пересечения плоскости α с ребром A₁B₁.
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

3. Сечением прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ плоскостью α, содержащей прямую BD₁ и параллельной прямой AC, является ромб.
а) Докажите, что грань ABCD— квадрат.
б) Найдите угол между плоскостями α и BCC₁, если AA₁=10, AB=12.

4. В правильной треугольной пирамиде SABC сторона основания AB=6, а боковое ребро SA=4. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Ответ: б) 8 + 2√2

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

5. В правильной треугольной пирамиде SABC сторона основания AB=60, а боковое ребро SA=37. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите расстояние от вершины A до плоскости α.
Ответ: б) 5√3

6. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.

7. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=6. Длины боковых рёбер пирамиды SA=3, SB=5, SD=3√5.
а) Докажите, что SA— высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
Ответ: б) 2,4

8. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=6. Длины боковых рёбер пирамиды SA=√21, SB=√85, SD=√57.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.

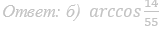
9. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB=5 и диагональю BD=9. Все боковые рёбра пирамиды равны 5.На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF=BE=4.
а) Докажите, что плоскость CEF параллельна ребру SB.
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

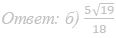
10. В правильной треугольной призме ABCA₁B₁C₁ сторона основания AB равна 6, а боковое ребро AA₁ равно 2√2. На рёбрах AB, A₁B₁ и B₁C₁отмечены точки M, N и K соответственно, причём AM = B₁N= C₁K=2.
а) Пусть L — точка пересечения плоскости MNK с ребром AC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
Ответ: б) 15

11. В правильной треугольной призме ABCA₁B₁C₁ сторона AB основания равна 6, а боковое ребро AA₁=3. На ребре AB отмечена точка K так, что AK=1. Точки M и L— середины рёбер A₁C₁ и B₁C₁соответственно. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) 3/4

12. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона AB основания равна 8, а боковое ребро AA₁ равно 4√2. На рёбрах BC и C₁D₁ отмечены точки K и L соответственно, причём BK= C₁L=2. Плоскость γ параллельна прямой BD и содержит точки K и L.
а) Докажите, что прямая A₁C перпендикулярна плоскости γ.
б) Найдите расстояние от точки B до плоскости γ.

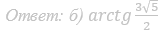
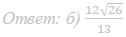
17. В правильной четырехугольной пирамиде SABCD сторона основания АВ равна 16, а высота равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM=DN=4 и АК=3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки К до плоскости SBC.

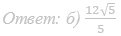
18. В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а высота равна 1. На ребрах АВ, АС и AS отмечены точки М, N и К соответственно, причем АМ=AN=3 и AK=7/4.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.

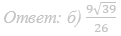
19. Основанием прямой четырехугольной призмы ABCDA₁B₁C₁D₁ является квадрат ABCD со стороной 4, высота призмы равна 6. Точка K делит ребро AA₁ в соотношении AK:KA₁=1:2. Через точки K и B проведена плоскость α, параллельная прямой AC и пересекающая ребро DD₁ в точке M.
а) Докажите, что плоскость α делит ребро DD₁ в отношении DM:MD₁=2:1.
б) Найдите площадь сечения.
Ответ: б) 8√6

20. В правильной треугольной призме ABCA₁B₁C₁ сторона AB основания равна 12, а боковое ребро AA₁ равно 3√6. На ребрах AB и B₁C₁ отмечены точки K и L соответственно, причем AK=2, B₁L=4. Точка M середина A₁C₁. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) √2

21. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=√5 и BC=2. Длины боковых рёбер пирамиды SA=√7, SB=2√3, SD=√11.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB.
Ответ: б) 30

22. В правильной четырехугольной пирамиде SABCD все ребра равны 5. На ребрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA=AQ=RC=2.
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.
Ответ: б) 7/2

23. В треугольной пирамиде PABC с основанием ABC известно, что AB=13, PB=15, cos PBA=48/65. Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Ответ: б) 90

25. Дана четырёхугольная пирамида SABCD с прямоугольником ABCD в основании. Сторона AB равна 4, а BC равна 4√2. Высота пирамиды проектируется в центр пересечения диагоналей прямоугольника. Из вершины A и C на ребро SB опущены перпендикуляры AP и CQ.
а) Докажите, что точка P является серединой отрезка BQ.
б) Найдите угол между плоскостями SBA и SBC, если ребро SD равно 8.

Видео:Построение проекции пирамиды. Метод прямого треугольника.Скачать

26. Дана пирамида PABCD, в основании — трапеция ABCD с большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K.
а) Доказать, что плоскость PAB перпендикулярна плоскости PCD.
б) Найдите объём PKBC, если AB = BC = CD = 2, а высота равна 12.
Ответ: б) 4

27. SABCD — правильная пирамида с вершиной S. Точка M расположена на SD так, что SM : SD = 2 : 3. P — середина ребра AD, а Q середина ребра BC.
а) Доказать, что сечение пирамиды плоскостью MQP — равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость MQP разбивает пирамиду.
Ответ: б) 2/7

28. В треугольной пирамиде SABC известны боковые рёбра SA=SB=7, SC=5. Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите объём пирамиды SABC.
Ответ: б) 16√6

29. На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM:BM = CN:NB = 1:2. Точки P и Q — середины сторон DA и DC соответственно.
а) Докажите, что P, Q, M и N лежат в плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
Ответ: б) 13/23

30. В основании прямой треугольной призмы ABCA₁B₁C₁ лежит прямоугольный треугольник ABC с прямым углом C, AC = 4, BC = 16, AA₁=4√2. Точка Q — середина ребра A₁B₁, а точка P делит ребро B₁C₁ в отношении 1 : 2, считая от вершины C₁. Плоскость APQ пересекает ребро CC₁ в точке M.
а) Докажите, что точка M является серединой ребра CC₁.
б) Найдите расстояние от точки A₁ до плоскости APQ.

32. В правильной треугольной призме ABCA₁B₁C₁ сторона AB основания равна 12, а высота призмы равна 2. На рёбрах B₁C₁ и AB отмечены точки P и Q соответственно, причём PC₁=3, а AQ = 4. Плоскость A₁PQ пересекает ребро BC в точке M.
а) Докажите, что точка M является серединой ребра BC.
б) Найдите расстояние от точки B до плоскости A₁PQ.

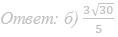
33. В правильной четырёхугольной пирамиде SABCD сторона AB основания равна 2√3, а высота SH пирамиды равна 3. Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды NSCD с вершиной N и основанием SCD.
а) Докажите, что точка T является серединой SM.
б) Найдите расстояние между NT и SC.
Ответ: б) √15/5

34. Дан прямой круговой конус с вершиной M. Осевое сечение конуса — треугольник с углом 120◦ при вершине M. Образующая конуса равна 2√3. Через точку M проведено сечение конуса, перпендикулярное одной из образующих.
а) Докажите, что получившийся в сечении треугольник тупоугольный.
б) Найдите площадь сечения.
Ответ: б) 4√2

35. Основанием прямой четырехугольной призмы ABCDA₁B₁C₁D₁ является квадрат ABCD со стороной 5√2, высота призмы равна 2√14. Точка K — середина ребра BB₁. Через точки K и C₁ проведена плоскость α, параллельная прямой BD₁.
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
Ответ: б) 26

36. Дана правильная пирамида SABCD. Точка M находится на SD так, что MS:SD=2:3. Точка P середина AD. Точка Q середина BC.
а) Доказать, что сечение пирамиды плоскостью MQP – равнобедренная трапеция.
б) Найдите соотношение объемов.
Ответ: б) 2/7

39. В правильной треугольной призме ABCA₁B₁C₁ сторона основания АВ=6, а боковое ребро AA₁ =3. На ребре B₁C₁ отмечена точка L так, что B₁L=1. Точки К и М – середины ребер АВ и A₁C₁ соответственно. Плоскость ƴ параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости ƴ
б) Найдите объем пирамиды, вершина которой – точка М, а основание – сечение данной призмы плоскостью ƴ.
Ответ: б) 5√3

40. В правильной четырехугольной призме KLMNK₁L₁M₁N₁ точка E делит боковое ребро KK₁ в отношении KE:EK₁=1:3. Через точки L и E проведена плоскость α параллельная прямой KM и пересекающая ребро NN₁ в точке F.
а) Докажите, что плоскость α делит ребро NN₁ пополам.
б) Найдите угол между плоскостью α и плоскостью грани KLMN, если известно, что KL = 6, KK₁=4.

44. В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB=BC=AC=5√2.
а) Докажите, что эта пирамида правильная.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA=DN:NC=2:3. Найдите площадь сечения MNB.
Ответ: б) 3√6

45. В основании правильной треугольной пирамиды ABCD лежит треугольник ABC со стороной, равной 6. Боковое ребро пирамиды равно 5. На ребре AD отмечена точка T так, что AT:TD=2:1. Через точку Т параллельно прямым AC и BD проведена плоскость.
а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.
б) Найдите площадь сечения.
Ответ: б) 20/3

46. Дан цилиндр, в котором проведены диаметры оснований. AB – диаметр верхнего основания, CD — диаметр нижнего, причем отрезки AB и CD не лежат на параллельных прямых.
а) Докажите, что у пирамиды ABCD противоположные ребра равны.
б) Найдите высоту цилиндра, если AC=7, AD=6, а радиус основания цилиндра равен 2,5.
Ответ: б) √30

47. SABCD — правильная пирамида с вершиной S. Из точки В опущен перпендикуляр BH на плоскость SAD.
а) Доказать, что угол AHC=90°.
б) Найдите объем пирамиды, если HA=1 и HC=7.

Видео:Построение сечения пирамиды по трем точкамСкачать

49. В одном основании прямого кругового цилиндра с высотой 3 и радиусом основания 8 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
Ответ: б) 64+32√3

52. В правильной четырёхугольной пирамиде PABCD сторона основания ABCD равна 12, боковое ребро PA ―12√2. Через вершину A проведена плоскость a, перпендикулярная прямой PC и пересекающая ребро PC в точке K.
а) Докажите, что плоскость a делит высоту PH пирамиды PABCD в отношении 2:1, считая от вершины P.
б) Найдите расстояние между прямыми PH и BK.

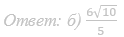
53. Дана правильная четырехугольная призма ABCDA₁B₁C₁D₁ . На ребре AA₁ отмечена точка K так, что AK: KA₁ = 1 : 2. Плоскость a проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD₁ в точке M.
а) Докажите, что MD:MD₁=2:1.
б) Найдите площадь сечения, если AB=4, AA₁=6.
Ответ: б) 8√6

54. На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:OB=1:2. Точка P — середина ребра AS.
а) Докажите, что плоскость DPQ перпендикулярна плоскости основания пирамиды.
б) Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
Ответ: б) √5

55. В правильном тетраэдре АВС точка Н — центр грани АВС, а точка М — середина ребра СD.
а) Докажите, что прямые АВ и СD перпендикулярны.
б) Найдите угол между прямыми DН и ВМ.

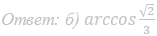
56. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C₁, причём CC₁ — образующая цилиндра, а AC — диаметр основания. Известно, что ∠ACB=30°, AB=√2, CC₁=2.
а) Докажите, что угол между прямыми AC₁ и BC равен 45°.
б) Найдите объём цилиндра.
Ответ: б) 4π

57. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки B₁ и C₁, причем BB₁ — образующая цилиндра, а отрезок AC₁ пересекает ось цилиндра.
а) Докажите, что угол ABC₁ прямой.
б) Найдите угол между прямыми BB₁ и AC₁, если АВ = 6, BB₁=15, B₁C₁=8.

58. В основании прямой треугольной призмы ABCA₁B₁C₁ . лежит равнобедренный (AB = BC) треугольник ABC. Точки K и M — середины рёбер A₁B₁ и AC соответственно.
а) Докажите, что KM = KB.
б) Найдите угол между прямой KM и плоскостью ABB₁, если AB = 8, AC = 6 и AA₁ = 3.

59. Дана правильная треугольная призма ABCA₁B₁C₁ , у которой сторон основания равна 2, а боковое ребро равно 3. Через точки A, C₁и середину T ребра A₁B₁ проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Ответ: б) arctg 3

61. В треугольной пирамиде SABC основанием является правильный треугольник ABC, а ребро SB перпендикулярно плоскости основания. Точки D, E и F середины ребер AB, BC и BS соответственно.
а) Докажите, что плоскость DEF делит пополам высоту пирамиды, проведенную из вершины B.
б) Найдите расстояние от точки B до плоскости DEF, если AB=6, AS=10.

62. В основании пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=√33, все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка Е, а на ребре AS – точка F так, что SF=BE=3.
а) Докажите, что плоскость CEF параллельна SB.
б) Пусть плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от Q до плоскости АВС.

63. Дана правильная четырехугольная пирамида MABCD, все ребра которой равны 12. Точка N – середина бокового ребра MA, точка K делит боковое ребро MB в отношении 2:1, считая от вершины M.
а) Докажите, что сечение пирамиды плоскостью, проходящей через точки N и K параллельно прямой AD, является равнобедренной трапецией.
б) Найдите площадь этого сечения.
Ответ: б) 7√51

64. На окружности основания конуса с вершиной S отмечены точки A, B и C так, что AB=BC. Медиана AM треугольника ASC пересекает высоту конуса.
а) Точка N — середина отрезка AC. Докажите, что MNB прямой.
б) Найдите угол между прямыми AM и SB, если AS=2, AC=√6.

65. В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 6. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды.
Ответ: б) 12√3

66. В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 5, а сторона основания равна 4. На продолжении ребра SA за точку A отмечена точка P, а на продолжении ребра SB за точку B —точка Q, причём AP = BQ = SA.
а) Докажите, что прямые PQ и SC перпендикулярны друг другу.
б) Найдите угол между плоскостями ABC и CPQ.

67. Плоскость α проходит через середину ребра AD прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ . перпендикулярно прямой BD₁.
а) Докажите, что угол между плоскостью α и плоскостью ABC равен углу между прямыми BB₁ и B₁D.
б) Найдите угол между плоскостью α и плоскостью ABC, если объём параллелепипеда ABCDA₁B₁C₁D₁ равен 48√3, AB = 2√3 и AD = 6.
Ответ: б) 60°

Видео:Построение сечений (часть 1). Пирамиды. сечениеСкачать

69. Дана пирамида SABC в которой SC=SB=AB=AC=√17, SA=BC=2√5.

а) Докажите, что ребро SA перпендикулярно ребру BC.

б) Найдите расстояние между ребрами BC и SA.

а) Докажите, что расстояние от вершины A1 до прямой BK равно ребру куба.

б) Найдите угол между плоскостями KBA1 и BCC1.

а) Докажите, что прямая KL проходит через середину ребра BC.

б) Найдите угол между прямыми AD1 и KL, если AB=2√2, AD=6, AA1=8.

72. На ребре AB правильной треугольной пирамиды SABC с основанием ABC отмечена точка K, причём AK=15, BK=3. Через точку K проведена плоскость α, параллельная плоскости SBC.

а) Докажите, что плоскость α проходит через середину высоты пирамиды.

б) Найдите расстояние между плоскостями α и SBC, если высота пирамиды равна 13.

73. В правильной треугольной пирамиде SABC точка P – делит сторону AB в отношении 2:3 считая от вершины A, точка K – делит сторону BC в отношении 2:3 считая от вершины C. Через точки P и K параллельно SB проведена плоскость a.

а) Докажите, что сечение пирамиды плоскостью a является прямоугольником.

б) Найдите расстояние от точки S до плоскости a если известно, что SC=5, AC=6.

74. В правильной треугольной пирамиде SABC сторона основания AB=9, а боковое ребро SA=6. На ребрах AB и SC отмечены точки K и M соответственно, причем AK : KB=SM : MC =2:7. Плоскость a содержит прямую KM и параллельна прямой SA.

а) Докажите, что плоскость a делит ребро SB в отношении 2:7 считая от вершины S.

б) Найдите расстояние между прямыми SA и KM.

Видео:Пирамида. 11 класс.Скачать

75. В правильной четырехугольной пирамиде SABCD сторона основания AB=3, а боковое ребро SA=6. Точка K делит ребро SC, причем SK:KC=1:2. Плоскость a проходит через точку K и параллельна SAD.

а) Докажите, что сечение пирамиды плоскость a является равнобедренной трапецией.

б) Найдите объем пирамиды, вершиной которой является точка S, а основание – сечение пирамиды SABC плоскость a.

📹 Видео

№55,б Пересечение пирамиды плоскостью общего положенияСкачать

№241. Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 мСкачать

Лекция 5 Задача 4Скачать

№3. Как строить сечения пирамидСкачать

10 класс, 32 урок, ПирамидаСкачать

Как правильно построить сечение пирамиды плоскостью.Скачать

Определение точек встречи прямой с многогранником (пирамида, призма)Скачать

ЕГЭ Задание 14 Пирамида вписана в сферуСкачать

Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основанияСкачать

Построение проекции пирамиды в трех плоскостях и построение точек 1 и 2, свободно расположенных в ееСкачать

Начертательная геометрия. 14 урок. Пересечение пирамиды плоскостью общего положенияСкачать

Усеченная пирамида. 11 класс.Скачать

Усеченная пирамида Построение сечения, изометрии и развертки поверхности пошаговоСкачать

Объём пирамидыСкачать