- Вариант 1 Вариант 2 Использован шаблон создания тестов в
- Результат теста Верно: 14 Ошибки: 0
- Вариант 1 б) FK>FM а) FM>AF в)
- Вариант 1 2. ВF┴(АВС). Прямые
- Вариант 1 в) высотой а) биссектрисой б) медианой 5 3
- Вариант 1 б) ОС а) СD 4. АВСD – прямоугольник,
- Треугольник. Медиана, биссектриса, высота, средняя линия.
- теория по математике 📈 планиметрия
- Виды треугольников по углам
- Виды треугольников по сторонам
- Медиана, биссектриса, высота, средняя линия треугольника
- Медиана
- Биссектриса
- Высота
- Средняя линия
- § 3. Четыре замечательные точки треугольника
- Свойства биссектрисы угла
- Свойства серединного перпендикуляра к отрезку
- Теорема о пересечении высот треугольника
- Задачи
- Ответы к задачам
- 💥 Видео
Видео:№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать

Вариант 1 Вариант 2 Использован шаблон создания тестов в
Использован шаблон создания тестов в PowerPoint
МКОУ «Погорельская СОШ» Кощеев М.М.
Тест по теме:
«Перпендикуляр и наклонные. Теорема о трех перпендикулярах. Угол между прямой и плоскостью»
Видео:№681. Серединный перпендикуляр к стороне АВ равнобедренного треугольника ABC пересекаетСкачать

Результат теста Верно: 14 Ошибки: 0
Верно: 14
Ошибки: 0
Отметка: 5
Время: 0 мин. 27 сек.
Видео:Перпендикуляр от точки к плоскостиСкачать
Вариант 1 б) FK>FM а) FM>AF в)
б) FK>FM
а) FM>AF
в) АК
1. АF┴α, Неверно , что……
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

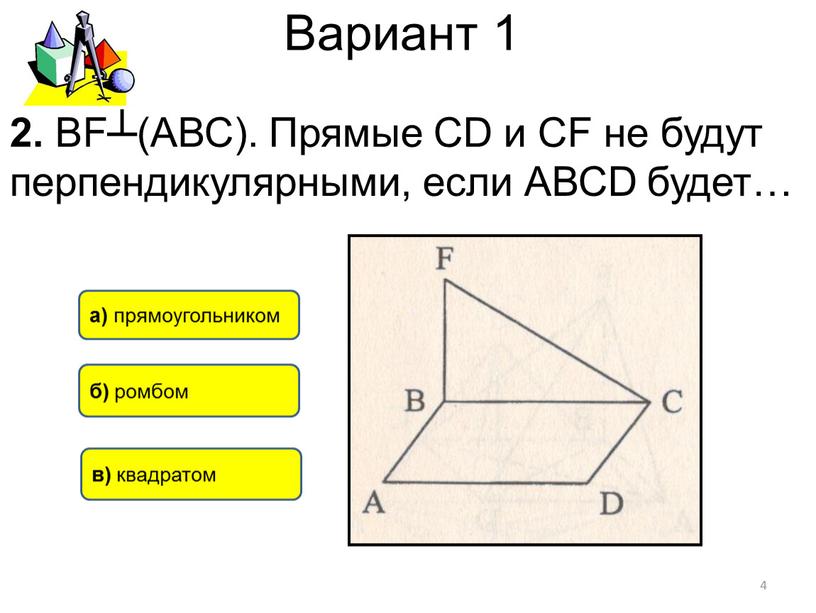
Вариант 1 2. ВF┴(АВС). Прямые
2. ВF┴(АВС). Прямые СD и CF не будут
перпендикулярными, если АВСD будет…
б) ромбом
а) прямоугольником
в) квадратом
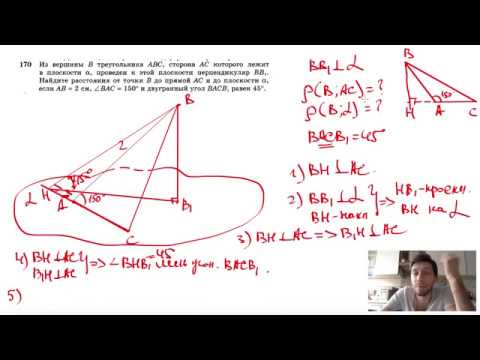
Видео:№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать
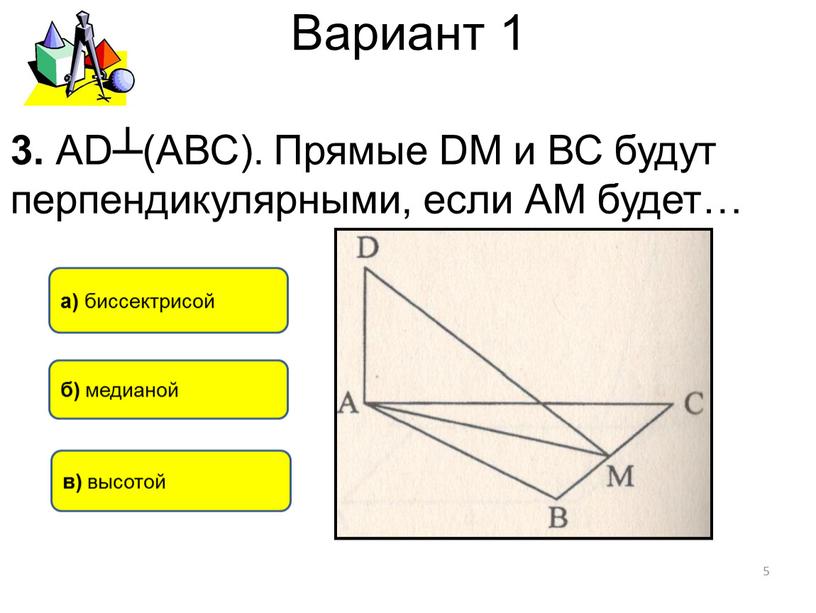
Вариант 1 в) высотой а) биссектрисой б) медианой 5 3
в) высотой
а) биссектрисой
б) медианой
3. АD┴(АВС). Прямые DM и ВС будут перпендикулярными, если АМ будет…
Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

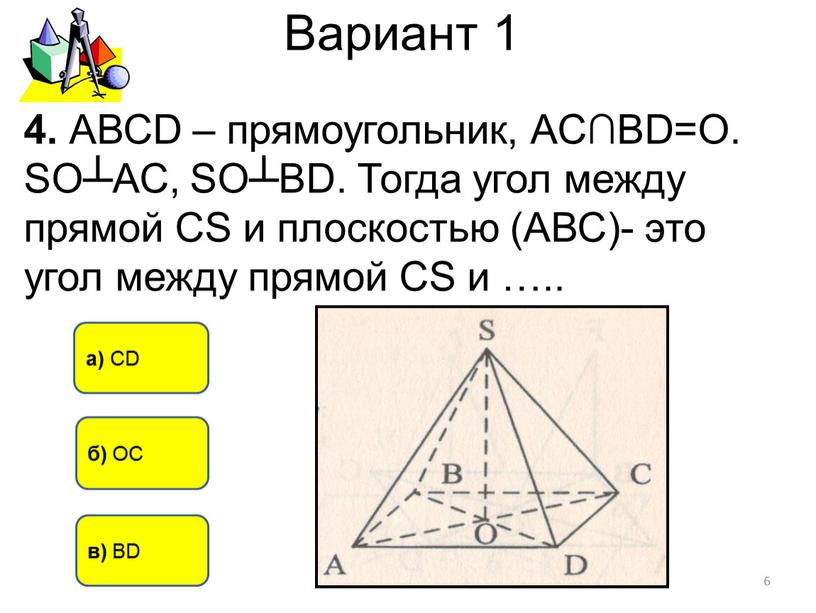
Вариант 1 б) ОС а) СD 4. АВСD – прямоугольник,
б) ОС
а) СD
4. АВСD – прямоугольник, АС∩BD=О. SO┴АС, SO┴BD. Тогда угол между прямой CS и плоскостью (АВС)- это угол между прямой CS и …..
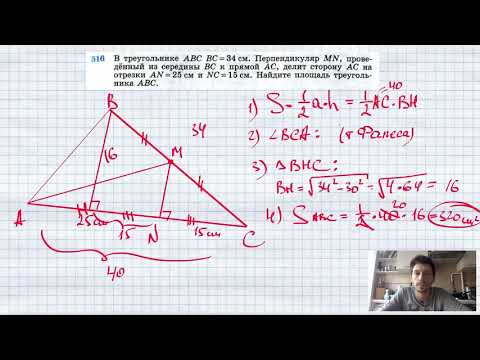
Видео:№516. В треугольнике ABC ВС = 34 см. Перпендикуляр MN, проведенный из середины ВС к прямой АССкачать
Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
| Остроугольные | Тупоугольные | Прямоугольные |
| Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС. | Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой. | Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный. |
 |  |  |
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |  |  |
Видео:№680. Серединные перпендикуляры к сторонам АВ и АС треугольника ABC пересекаются в точке DСкачать
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .
Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .
Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Серединные перпендикуляры в треугольникеСкачать
§ 3. Четыре замечательные точки треугольника
Свойства биссектрисы угла
Докажем сначала теорему о биссектрисе угла.
| Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон 1 . Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе. |
1) Возьмём произвольную точку М на биссектрисе угла ВАС, проведём перпендикуляры МК и ML к прямым АВ и АС и докажем, что MK = ML (рис. 224). Рассмотрим прямоугольные треугольники AM К и AML. Они равны по гипотенузе и острому углу (AM — общая гипотенуза, ∠1 = ∠2 по условию). Следовательно, MK = ML.
2) Пусть точка М лежит внутри угла ВАС и равноудалена от его сторон АВ и АС. Докажем, что луч AM — биссектриса угла ВАС (см. рис. 224). Проведём перпендикуляры МК и ML к прямым АВ и АС. Прямоугольные треугольники АМК и AML равны по гипотенузе и катету (AM — общая гипотенуза, МК = ML по условию). Следовательно, ∠1 = ∠2. Но это и означает, что луч AM — биссектриса угла ВАС. Теорема доказана.
| Геометрическим местом точек плоскости, лежащих внутри неразвёрнутого угла и равноудалённых от сторон угла, является биссектриса этого угла. |
| Биссектрисы треугольника пересекаются в одной точке. |
В самом деле, обозначим буквой О точку пересечения биссектрис АА1 и ВВ1 треугольника АВС и проведём из этой точки перпендикуляры OK, OL и ОМ соответственно к прямым АВ, ВС и СА (рис. 225). По доказанной теореме ОК = ОМ и OK = OL. Поэтому ОМ = OL, т. е. точка О равноудалена от сторон угла АСВ и, значит, лежит на биссектрисе СС1 этого угла. Следовательно, все три биссектрисы треугольника АВС пересекаются в точке О, что и требовалось доказать.
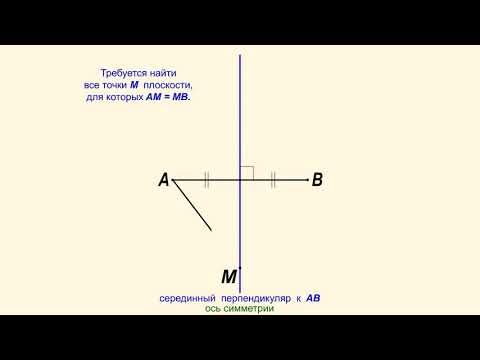
Свойства серединного перпендикуляра к отрезку
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
На рисунке 226 прямая а — серединный перпендикуляр к отрезку АВ.
Докажем теорему о серединном перпендикуляре к отрезку.
| Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему. |
Пусть прямая m — серединный перпендикуляр к отрезку АВ, точка О — середина этого отрезка (рис. 227, а).
1) Рассмотрим произвольную точку М прямой m и докажем, что AM = ВМ. Если точка M совпадает с точкой О, то это равенство верно, так как О — середина отрезка АВ. Пусть M и О различные точки. Прямоугольные треугольники ОAM и ОВМ равны по двум катетам (ОА = ОВ, ОМ — общий катет), поэтому AM = ВМ.
2) Рассмотрим произвольную точку N, равноудалённую от концов отрезка АВ, и докажем, что точка N лежит на прямой m. Если N — точка прямой АВ, то она совпадает с серединой О отрезка АВ и потому лежит на прямой m. Если же точка N не лежит на прямой АВ, то треугольник ANB равнобедренный, так как AN = BN (рис. 227, б). Отрезок NO — медиана этого треугольника, а значит, и высота. Таким образом, NO ⊥ АВ, поэтому прямые ON и m совпадают, т. е. N — точка прямой m. Теорема доказана.
| Геометрическим местом точек плоскости, равноудалённых от концов отрезка, является серединный перпендикуляр к этому отрезку. |
| Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. |
Для доказательства этого утверждения рассмотрим серединные перпендикуляры m и n к сторонам АВ и ВС треугольника АВС (рис. 228). Эти прямые пересекаются в некоторой точке О. В самом деле, если предположить противное, т. е. что m || n, то прямая ВА, будучи перпендикулярной к прямой m, была бы перпендикулярна и к параллельной ей прямой n, а тогда через точку В проходили бы две прямые ВА и ВС, перпендикулярные к прямой n, что невозможно.
По доказанной теореме ОВ = ОА и ОВ = ОС. Поэтому ОА = ОС, т. е. точка О равноудалена от концов отрезка АС и, значит, лежит на серединном перпендикуляре р к этому отрезку. Следовательно, все три серединных перпендикуляра m, n и р к сторонам треугольника АВС пересекаются в точке О.
Теорема о пересечении высот треугольника
Мы доказали, что биссектрисы треугольника пересекаются в одной точке, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Ранее было доказано, что медианы треугольника пересекаются в одной точке (п. 64). Оказывается, аналогичным свойством обладают и высоты треугольника.
| Высоты треугольника (или их продолжения) пересекаются в одной точке. |
Рассмотрим произвольный треугольник АВС и докажем, что прямые АА1 ВВ1 и СС1 содержащие его высоты, пересекаются в одной точке (рис. 229).
Проведём через каждую вершину треугольника АВС прямую, параллельную противоположной стороне. Получим треугольник А2В2С2. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А2С и АВ = СВ2 как противоположные стороны параллелограммов АВА2С и АВСВ2, поэтому А2С = СВ2. Аналогично С2А = АВ2 и С2В = ВА2. Кроме того, как следует из построения, СС1 ⊥ А2В2, АА1 ⊥ В2С2 и ВВ1 ⊥ А2С2. Таким образом, прямые АА1, ВВ1 и СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2. Следовательно, оНи пересекаются в одной точке. Теорема доказана.
Итак, с каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.
Задачи
674. Из точки М биссектрисы неразвёрнутого угла О проведены перпендикуляры МА и МВ к сторонам этого угла. Докажите, что АВ ⊥ ОМ.
675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке А. Докажите, что центры этих окружностей лежат на прямой О А.
676. Стороны угла А касаются окружности с центром О радиуса r. Найдите: а) ОА, если r = 5 см, ∠A = 60°; б) г, если ОА = 14 дм, ∠A = 90°.
677. Биссектрисы внешних углов при вершинах В и С треугольника АВС пересекаются в точке О. Докажите, что точка О является центром окружности, касающейся прямых АВ, ВС, АС.
678. Биссектрисы АА1 и ВВ1 треугольника АВС пересекаются в точке М. Найдите углы ACM и ВСМ, если: a) ∠AMB = 136°; б) ∠AMB = 111°.
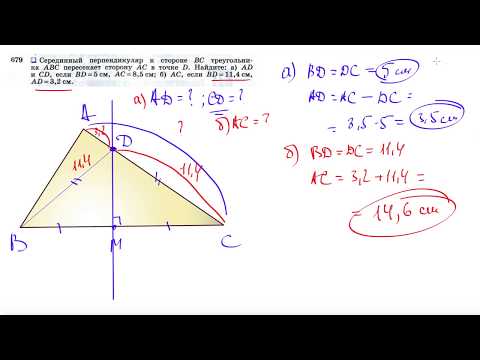
679. Серединный перпендикуляр к стороне ВС треугольника АВС пересекает сторону АС в точке D. Найдите: a) AD и CD, если BD = 5 см, Ас = 8,5см; б) АС, если BD = 11,4 см, AD = 3,2 см.
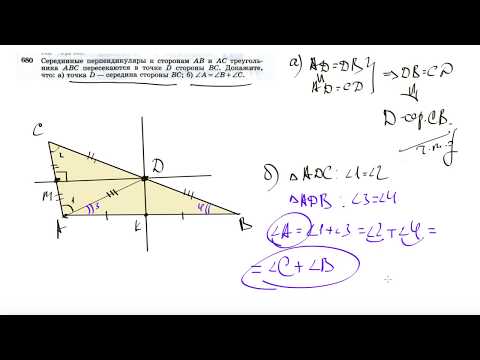
680. Серединные перпендикуляры к сторонам АВ и АС треугольника АВС пересекаются в точке D стороны ВС. Докажите, что: а) точка D — середина стороны ВС; б) ∠A — ∠B + ∠C.
681. Серединный перпендикуляр к стороне АВ равнобедренного треугольника АВС пересекает сторону ВС в точке Е. Найдите основание АС, если периметр треугольника АЕС равен 27 см, а АВ = 18 см.
682. Равнобедренные треугольники АВС и ABD имеют общее основание АВ. Докажите, что прямая CD проходит через середину отрезка АВ.
683. Докажите, что если в треугольнике АВС стороны АВ и АС не равны, то медиана AM треугольника не является высотой.
684. Биссектрисы углов при основании АВ равнобедренного треугольника АВС пересекаются в точке М. Докажите, что прямая СМ перпендикулярна к прямой АВ.
685. Высоты АА1 и ВВ1 равнобедренного треугольника АВС, проведённые к боковым сторонам, пересекаются в точке М. Докажите, что прямая МС — серединный перпендикуляр к отрезку АВ.
686. Постройте серединный перпендикуляр к данному отрезку.
Пусть АВ — данный отрезок. Построим две окружности с центрами в точках А и В радиуса АВ (рис. 230). Эти окружности пересекаются в двух точках М1 и М2. Отрезки АМ1, AM2, ВМ1, ВМ2 равны друг другу как радиусы этих окружностей.
Проведём прямую М1М2. Она является искомым серединным перпендикуляром к отрезку АВ. В самом деле, точки М1 и М2 равноудалены от концов отрезка АВ, поэтому они лежат на серединном перпендикуляре к этому отрезку. Значит, прямая М1М2 и есть серединный перпендикуляр к отрезку АВ.
687. Даны прямая а и две точки А и В, лежащие по одну сторону от этой прямой. На прямой а постройте точку М, равноудалённую от точек А к В.
688. Даны угол и отрезок. Постройте точку, лежащую внутри данного угла, равноудалённую от его сторон и равноудалённую от концов данного отрезка.
Ответы к задачам
674. Указание. Сначала доказать, что треугольник АОВ равнобедренный.
676. а) 10 см; б) 7√2 дм.
678. а) 46° и 46°; б) 21° и 21°.
679. a) АВ = 3,5 см, CD = 5 см; б) АС = 14,6 см.
683. Указание. Воспользоваться методом доказательства от противного.
687. Указание. Воспользоваться теоремой п. 75.
688. Указание. Учесть, что искомая точка лежит на биссектрисе данного угла.
1 То есть равноудалена от прямых, содержащих стороны угла.
💥 Видео
№149. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,Скачать

Построение медианы в треугольникеСкачать

8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Почему серединные перпендикуляры пересекаются в одной точке? | Vasily mathsСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Геометрия В треугольнике ABC проведен серединный перпендикуляр его биссектрисы BD, которыйСкачать
№679. Серединный перпендикуляр к стороне ВС треугольника ABC пересекает сторону АС в точке DСкачать
Построение серединных перпендикуляров треугольника с помощью циркуляСкачать

Серединный перпендикулярСкачать