Перпендикулярные параллельные прямые координатная плоскость

Мерзляк 6 класс Контрольная 11 в 4-х вариантах. Контрольная работа по математике в 6 классе «Перпендикулярные и параллельные прямые. Осевая и центральная симметрии. Координатная плоскость». Методическое пособие для УМК Мерзляк, Полонский, Якир. Цитаты из пособия использованы в учебных целях. Ответов нет!

Математика 6 класс (Мерзляк)
Контрольная работа № 11

Перпендикулярные и параллельные прямые. Осевая и центральная симметрии. Координатная плоскость

Вариант 1

1. Перерисуйте в тетрадь рисунок 3. Проведите через точку C:
   1) прямую а, параллельную прямой m;
   2) прямую b, перпендикулярную прямой m.
2. Начертите произвольный треугольник ABC. Постройте фигуру, симметричную этому треугольнику относительно точки A.
3. Отметьте на координатной плоскости точки A (–1; 4) и B (–4; –2). Проведите отрезок AB.
   1) Найдите координаты точки пересечения отрезка AB с осью абсцисс.
   2) Постройте отрезок, симметричный отрезку AB относительно оси ординат, и найдите координаты концов полученного отрезка.
4. Начертите тупой угол BDK, отметьте на его стороне DK точку M. Проведите через точку M прямую, перпендикулярную прямой DK, и прямую, перпендикулярную прямой DB.
5. Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 4 изображён график движения туриста.
   1) На каком расстоянии от лагеря был турист через 4 ч после начала движения?
   2) Сколько времени турист затратил на остановку?
   3) Через сколько часов после начала движения турист был на расстоянии 12 км от лагеря?
   4) С какой скоростью шёл турист до остановки?
6. Даны координаты трёх вершин прямоугольника ABCD: A (–2; –3), B (–2; 5) и C (4; 5).
   1) Начертите этот прямоугольник.
   2) Найдите координаты вершины D.
   3) Найдите координаты точки пересечения диагоналей прямоугольника.
   4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (х; у) такие, что х = 2, у — произвольное число.

Вариант 2

1. Перерисуйте в тетрадь рисунок 5. Проведите через точку F:
   1) прямую а, параллельную прямой с;
   2) прямую b, перпендикулярную прямой с.
2. Начертите произвольный треугольник DEF. Постройте фигуру, симметричную этому треугольнику относительно точки E.
3. Отметьте на координатной плоскости точки C (1; 4) и D (–1; 2). Проведите отрезок CD.
   1) Найдите координаты точки пересечения отрезка CD с осью ординат.
   2) Постройте отрезок, симметричный отрезку CD относительно оси абсцисс, и найдите координаты концов полученного отрезка.
4. Начертите тупой угол OCA, отметьте на его стороне CA точку P. Проведите через точку P прямую, перпендикулярную прямой CA, и прямую, перпендикулярную прямой CO.
5. Велосипедист выехал из дома и через некоторое время вернулся назад. На рисунке 6 изображён график движения велосипедиста.
   1) На каком расстоянии от дома был велосипедист через 4 ч после начала движения?
   2) Сколько времени велосипедист затратил на остановку?
   3) Через сколько часов после начала движения велосипедист был на расстоянии 24 км от дома?
   4) С какой скоростью ехал велосипедист до остановки?
6. Даны координаты трёх вершин прямоугольника ABCD: A (–1; –3), C (5; 1) и D (5; –3).
   1) Начертите этот прямоугольник.
   2) Найдите координаты вершины B.
   3) Найдите координаты точки пересечения диагоналей прямоугольника.
   4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (х; у) такие, что у = –4, х — произвольное число.

Мерзляк 6 класс Контрольная 11. Вариант 3

1. Перерисуйте в тетрадь рисунок 7. Про ведите через точку B:
   1) прямую b, параллельную прямой а;
   2) прямую с, перпендикулярную прямой а.
2. Начертите произвольный треугольник MKP. Постройте фигуру, симметричную этому треугольнику относительно точки P.
3. Отметьте на координатной плоскости точки М (1; 2) и N (–1; 6). Проведите отрезок MN.
   1) Найдите координаты точки пересечения отрезка MN с осью ординат.
   2) Постройте отрезок, симметричный отрезку MN относительно оси абсцисс, и найдите координаты концов полученного отрезка.
4. Начертите тупой угол MCK, отметьте на его стороне CM точку A. Проведите через точку A прямую, перпендикулярную прямой CM, и прямую, перпендикулярную прямой CK.
5. Велосипедист выехал из дома и через некоторое время вернулся назад. На рисунке 8 изображён график движения велосипедиста.
   1) На каком расстоянии от дома был велосипедист через 3 ч после начала движения?
   2) Сколько времени велосипедист затратил на остановку?
   3) Через сколько часов после начала движения велосипедист был на расстоянии 30 км от дома?
   4) С какой скоростью ехал велосипедист до остановки?
6. Даны координаты трёх вершин прямоугольника ABCD: A (–2; –2), B (–2; 4) и D (6; –2).
   1) Начертите этот прямоугольник.
   2) Найдите координаты вершины C.
   3) Найдите координаты точки пересечения диагоналей прямоугольника.
   4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (х; у) такие, что х = –4, у — произвольное число.

Вариант 4

1. Перерисуйте в тетрадь рисунок 9. Проведите через точку M:
   1) прямую а, параллельную прямой b;
   2) прямую с, перпендикулярную прямой b.
2. Начертите произвольный треугольник ADK. Постройте фигуру, симметричную этому треугольнику относительно точки D.
3. Отметьте на координатной плоскости точки K (1; –1) и M (4; 2). Проведите отрезок KM.
   1) Найдите координаты точки пересечения отрезка KM с осью абсцисс.
   2) Постройте отрезок, симметричный отрезку KM относительно оси ординат, и найдите координаты концов полученного отрезка.
4. Начертите тупой угол APR, отметьте на его стороне PR точку E. Проведите через точку E прямую, перпендикулярную прямой PR, и прямую, перпендикулярную прямой AP.
5. Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 10 изображён график движения туриста.
   1) На каком расстоянии от лагеря был турист через 2 ч после начала движения?
   2) Сколько времени турист затратил на остановку?
   3) Через сколько часов после начала движения турист был на расстоянии 5 км от лагеря?
   4) С какой скоростью шёл турист до остановки?
6. Даны координаты трёх вершин прямоугольника ABCD: B (–3; 6); C (5; 6) и D (5; –2).
   1) Начертите этот прямоугольник.
   2) Найдите координаты вершины A.
   3) Найдите координаты точки пересечения диагоналей прямоугольника.
   4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (х; у) такие, что у = 3, х — произвольное число.

Вы смотрели: Мерзляк 6 класс Контрольная 11 в 4-х вариантах. Контрольная работа по математике в 6 классе «Перпендикулярные и параллельные прямые. Осевая и центральная симметрии. Координатная плоскость» УМК Мерзляк, Полонский, Якир. Цитаты из пособия «Математика 6 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Видео:Перпендикулярные прямые. 6 класс.Скачать

Презентация по математике по теме: Перпендикулярные и параллельные прямые. Координатная плоскость. Графики.

Видео:МЕРЗЛЯК-6. КОНТРОЛЬНАЯ РАБОТА-11. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. КООРДИНАТНАЯ ПЛОСКОСТЬ.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Урок закрепления знаний по темам: Перпендикулярные и параллельные прямые. Координатная плоскость. Графики.

Цели: повторить основные понятия и определения по темам; обобщить и систематизировать знания учащихся; подготовка к контрольной работе. Задачи: обобщить и систематизировать сведения о прямоугольной системе координат, параллельных и перпендикулярных прямых, графиках; отрабатывать умение определять координаты точки, строить точки по заданным координатам, строить параллельные и перпендикулярные прямые, читать графики; воспитывать самостоятельность, аккуратность, точность выполнения заданий; чувство коллективизма; развивать логическое мышление, память, внимание, культуру речи.

А В С D Вспомним правила построения параллельных прямых AB CD

Вспомним правило построения перпендикулярных прямых. Запись: АB a

. М m а 1) а ǀǀ m b 2) b l m Задание №1: Проведите через точку М: прямую а, параллельную m; прямую b, перпендикулярную m.

В М С . В1 . М1 ∆ ВМС симметричен ∆В1М1С относительно т.С Задание №2: Начертите произвольный треугольник BMC . Постройте фигуру, симметричную данному треугольнику относительно т.С

№3. Отметьте на координатной плоскости точки K(1;-1) и M(4;2). Проведите отрезок KM. 1) Найдите координаты точки пересечения отрезка KM с осью абсцисс. 2) Постройте отрезок, симметричный отрезку KM относительно оси ординат, и найдите координаты концов полученного отрезка. . К . М . Р 1) Р(2;0) . К1 . М1 2) К1М1 симметричен КМ относительно ОУ К1(-1;-1), М1(-4;2)

4. Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке изображен график движения туриста. 1)На каком расстоянии от лагеря был турист через 2 ч после начала движения? 2)Сколько времени турист затратил на остановку? 3)Через сколько часов после начала движения турист был на расстоянии 5км от лагеря? 4)С какой скоростью шел турист до остановки? 1) 10 км 2) 5 часов 3) Через 1ч и через 8 ч 4) S=10 км, t=2 ч V=S:t=10:2=5(км/ч)

Задание №5. Даны координаты вершин прямоугольника АВСD: А(-3;2), В(-3;6), D(5;2) а) Начертите этот прямоугольник; б) найдите координаты вершины C; в)найдите координаты точки пересечения диагоналей прямоугольника; г)найдите S и Р прямоугольника, считая, что длина ед.отрезка равна 1 см. . А . В . D С . б) С (5; 6) Е в) Е( 1;4) г) S = ВС*АВ= = 8*4=32 (см2) Р=2(АВ+ВС)= =2(4+8)=24 (см)

Успешного выполнения контрольной работы.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 953 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 330 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Данная презентация разработана в период дистанционного обучения в качестве завершающего урока по блоку: Параллельные и перпендикулярные прямые. Координатная плоскость. Графики. Задачами данного урока являются систематизация знаний и отработка умений по данному блоку тем. Основная цель данного урока — подготовка к контрольной работе.

• Туголукова Любовь АлександровнаНаписать 489 25.05.2020

Номер материала: ДБ-1178595

25.05.2020 0

25.05.2020 0

25.05.2020 0

25.05.2020 0

23.05.2020 0

23.05.2020 0

22.05.2020 0

22.05.2020 0

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Липецкой области начинающие педагоги получат 120 тысяч рублей

Время чтения: 0 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения создает цифровую психологическую службу для школьников

Время чтения: 1 минута

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ПЕРПЕНДИКУЛЯРНЫЕ и ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. КООРДИНАТНАЯ ПЛОСКОСТЬ. Контрольная №11. 6 классСкачать

Прямые на координатной плоскости

Линейная функция

График линейной функции

Прямые, параллельные оси ординат

Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

Видео:Параллельные прямые. 6 класс.Скачать

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

Видео:Перпендикулярные и параллельные прямые. Математика 6 классСкачать

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

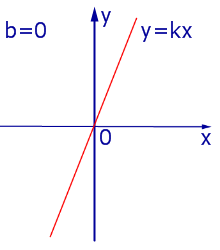Рис.1

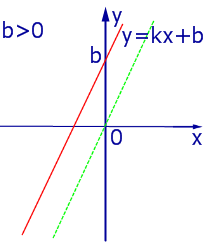Рис.2

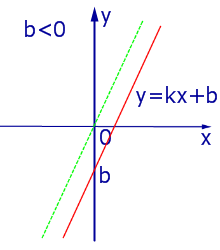Рис.3

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

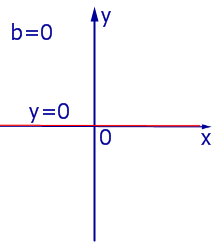Рис.4

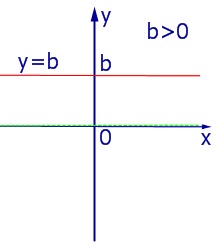Рис.5

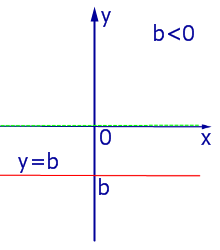Рис.6

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны . имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов. y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии y = kx (2) равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2). Рис.10 Рис.11 Рис.12 Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле Видео:Перпендикулярные и параллельные прямые. Координатная плоскость.Скачать Прямые, параллельные оси ординат Прямые, параллельные оси Oy , задаются формулой x = c , (3) где c – произвольное число, и изображены на рис. 13, 14, 15. Рис.13 Рис.14 Рис.15 Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:Перпендикулярные и параллельные прямые. Координатная плоскость. 6 классСкачать Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые px + qy = r , (4) где p, q, r – произвольные числа. В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию . что и требовалось. В случае, когда получаем: откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид 0 = r , (5) и при r = 0 его решением являются точки всей плоскости: В случае, когда уравнение (5) решений вообще не имеет. Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением px + qy = r1 , (6) параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением – qx + py = r2 , (7) перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и параллельной к прямой 4x + 5y = 7 ; (8) перпендикулярной к прямой (8). В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде 4x + 5y = r1 , (9) где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде – 5x + 4y = r2 , (10) где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство 🎦 Видео Перпендикулярные и параллельные прямые. Координатная плоскость.Скачать Перпендикулярные прямые. Практическая часть. 6 класс.Скачать Математика 6 класс. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. КООРДИНАТЫ НА ПЛОСКОСТИ. ГРАФИКИ.Скачать 6 класс, Мерзляк, К.р.11, В-1.Перпендикулярные и параллельные прямые.Координатная плоскость. ГрафикиСкачать Параллельные прямые | Математика | TutorOnlineСкачать Математика 6 класс: Параллельные и перпендикулярные прямыеСкачать Параллельные и перпендикулярные прямые.Скачать Перпендикулярные прямые. Практическая часть. 6 класс.Скачать Тема ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕСкачать Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать Подготовка к КР «Перпендикулярные и параллельные прямые. Координатная плоскость. Графики» 6 классСкачать Плоскость. Пересекающиеся прямые. 6 класс.Скачать ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕСкачать Поделиться или сохранить к себе: Смотрите также 2 параллельные прямые пересекаются 3 прямой найди углы сумма которых данным углом равна 180 градусов 2 параллельные прямые пересечены 3 прямой то внутренние накрест лежащие углы равны 2 прямые параллельны одной и той же плоскости можно ли утверждать что эти прямые Четырехугольник у которого противолежащие стороны параллельны то есть лежат на параллельных прямых 1 вписанный угол опирающийся на полуокружность острый 2 если две параллельные прямые пересечены 1 даны 2 параллельные прямые и секущая построить окружность касающуюся всех 3 х прямых 1 из внутренних односторонних углов образованных при пересечении 2 параллельных прямых 3 прямой 1 из односторонних углов образованных при пересечении 2 параллельных прямых секущей в 4 раза больше