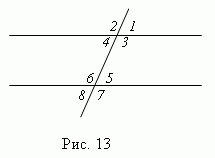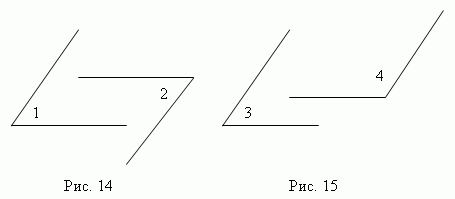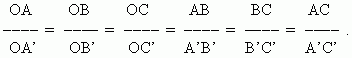Перпендикулярные прямые — это две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.
Содержание:
Понятие перпендикулярных прямых
При пересечении двух прямых есть очень важный случай, когда, пересекаясь, прямые образуют прямые углы (рис. 2.296).
Определение. Две прямые называют перпендикулярными, если они пересекаются под прямым углом.
На рисунках перпендикулярность прямых обозначается специальным знаком — 
При записи перпендикулярность прямых обозначается так: 
Запись 
Кроме понятия перпендикулярности прямых в геометрии используется понятие перпендикуляра к прямой. Говорят: провести перпендикуляр к прямой, проходящий через данную точку, опустить перпендикуляр из точки на прямую.
Определение. Перпендикуляром, проведенным из точки А к прямой а, называют отрезок прямой, перпендикулярной к прямой 

На рисунке 2.297 прямая АВ перпендикулярна к прямой 

Определение. Длину перпендикуляра, опущенного из данной точки на прямую, называют расстоянием от точки до прямой.
Построение перпендикулярных прямых связано с вычерчиванием прямых углов.
Для вычерчивания прямых углов используется угольник или чертежный треугольник (рис. 2.298). Прямой угол может быть изображен в любом положении (рис. 2.299).
На рисунке 2.300 показано, как с помощью угольника и линейки можно провести перпендикуляр через точку О, лежащую на прямой АВ. На рисунке 2.301 показано, как можно провести перпендикуляр с помощью угольника и линейки через точку О к прямой АВ при условии, что О не лежит на АВ.
Теорема 2. К данной прямой через данную точку можно провести только один перпендикуляр.
Серединный перпендикуляр отрезка
Определение. Прямую, проходящую через середину отрезка перпендикулярно ему, называют серединным перпендикуляром (рис. 2.302).
Свойства серединного перпендикуляра к отрезку:
— если точка равноудалена от концов отрезка, то она принадлежит серединному перпендикуляру этого отрезка;
— если точка принадлежит серединному перпендикуляру отрезка, то она равноудалена от его концов.
Можно доказать такую теорему.
Теорема 3. Множество точек плоскости, равноудаленных от концов отрезка, есть серединный перпендикуляр к этому отрезку.
Перпендикуляр и наклонная
Если есть точка и прямая, то по теореме 1 есть и плоскость, в которой они лежат, а значит, все рассуждения в данном случае будут связаны с той плоскостью, в которой лежат данные точка и прямая.
Пусть даны прямая 


В отличие от перпендикуляра наклонная образует с прямой, к которой она проведена, угол, отличный от 90°.
Можно доказать теорему.
Теорема 4. Расстояние от точки А до основания перпендикуляра, проведенного через нее к прямой 

Иначе говоря, перпендикуляр ВА короче, чем отрезок ВС любой наклонной.
Есть еще одно понятие, которым часто пользуются в данной ситуации, — это проекция точки на прямую. Даны прямая 




Можно, пользуясь понятием проекции точки на прямую, определить и проекцию фигуры на данную прямую. Например, на рисунке 2.304 изображена проекция отрезка на прямую 
Проекция отрезка есть тоже отрезок 
Пример:
Равные отрезки AD и СВ, заключенные между параллельными прямыми АС и BD, пересекаются в точке О. Докажите, что АО = СО и ВО = DO.
Решение:
Из условия задачи имеем:
3. AD и СВ пересекаются в точке О.
4. АО = СО и ВО = DO (требуется доказать).
Чтобы доказать п. 4, нужно доказать, что 

5. Проведем из точек А и С перпендикуляры к прямой BD (построение) (рис. 2.305).
6. АК = СМ (5, свойство расстояний между параллельными прямыми).
7. 
8. 
9. 
Аналогично можно доказать, что АО = СО.
Геометрическое место точек
В геометрии для описания некоторых геометрических фигур есть свое название — геометрическое место точек.
Определение. Геометрическим местом точек называют фигуру, которая состоит из всех точек плоскости, обладающих определенным свойством.
Например, окружность можно определить как геометрическое место точек плоскости, равноудаленных от данной точки. Серединный перпендикуляр отрезка можно также определить как геометрическое место точек плоскости, равноудаленных от концов этого отрезка.
В этих примерах говорится о геометрическом месте точек плоскости.
Геометрические места точек широко используются при решении геометрических задач на построение. Сущность метода геометрических мест, используемого при решении задач на построение, состоит в следующем.
Пусть для решения задачи на построение надо найти точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура 



Пример 1.
Даны три точки: А, В, С. Постройте точку X, которая одинаково удалена от точек А и В и находится на данном расстоянии от точки С.
1. Нам даны три точки А, В, С (рис. 2.306).
2. Искомая точка X удовлетворяет двум условиям: 1) она одинаково удалена от точек А и В; 2) она находится на данном расстоянии от точки С. Геометрическое место точек, удовлетворяющих первому условию, есть серединный перпендикуляр отрезка АВ (рис. 2.307).
3. Геометрическое место точек, удовлетворяющих второму условию, есть окружность данного радиуса с центром в точке С (рис. 2.308). Искомая точка X лежит на пересечении этих геометрических мест. В данном случае искомых точек две: 

Биссектриса угла также является очень важным и широко используемым геометрическим местом точек.
Пример 2.
Найдите геометрическое место точек, равноудаленных от сторон угла и находящихся в его внутренней области.
Решение:
А) Пусть точка принадлежит внутренней области угла и равноудалена от его сторон. Докажем, что эта точка принадлежит биссектрисе данного угла.

1. Точка М принадлежит внутренней области угла АОВ (рис. 2.309).
2. Проведем МК 

3. ОМ — биссектриса угла АОВ (требуется доказать).
У нас на чертеже нет луча ОМ, проведем его.
4. Соединим точки О и М (построение) (рис. 2.311).
Нам нужно доказать, что ОМ — биссектриса угла О или, что 

5. 
6. 
7. ОМ — биссектриса угла АОВ.
Б) Пусть точка принадлежит биссектрисе данного угла. Докажем, что эта точка равноудалена от сторон данного угла.
1. Пусть М — произвольная точка биссектрисы ОМ угла АОВ (рис. 2.312) (дано).
2. 
3. Проведем МК и МС — перпендикуляры к сторонам угла АОВ (рис. 2.313) (построение).
4. 
5. МК = МС. Точка М равноудалена от сторон угла (4).
Итак, геометрическим местом точек угла, равноудаленных от его сторон, является биссектриса этого угла.
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Видео:Перпендикулярные прямые. 6 класс.Скачать

Перпендикулярные отрезки заключенные между параллельными прямыми
Определение.1. Параллельные прямое
Определение.2. Перпендикулярные прямые
Теорема.1. I свойство параллельных прямых
Теорема.2. II свойство параллельных прямых
Теорема.3. III свойство параллельных прямых
Теорема.4. IV свойство параллельных прямых
Теорема.5. V свойство параллельных прямых
Теорема.6. I признак параллельных прямых
Теорема.7. II признак параллельных прямых
Теорема.8. III признак параллельных прямых
Теорема.9. IV признак параллельных прямых
Теорема 10. V признак параллельных прямых
Теорема 11. Две прямые, параллельные третей
Теорема 11.1 Следствие
Теорема 12. Прямая, пересекающая одну из параллельных прямых
Теорема 13. Отрезки параллельных прямых
Теорема 14. Теорема Фалеса
Теорема 14.1. Параллельные прямые, пересекающие стороны угла
Теорема 15. Прямая, перпендикулярна одной из параллельных прямых
Теорема 16. Две (и более) прямые, перпендикулярные третей прямой
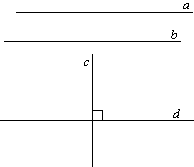
Определение 1. Параллельными называются прямые, которые не пересекаются, сколько бы мы их не продолжали.
На рисунке a и b.
Определение 2. Перпендикулярными называются прямые, которые пересекаются под прямым углом.
На рисунке c и d.
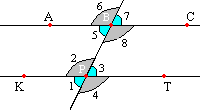
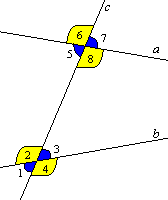
Внутренние накрестлежащие углы — 2 и 8; 3 и 5
Внешние накрестлежащие углы — 1 и 7; 4 и 6
Внутренние односторонние углы — 2 и 5; 3 и 8
Внешние односторонние углы — 1 и 6; 4 и 7
Соответственные углы — 1 и 5; 2 и 6; 3 и 7; 4 и 8
Между этими углами можно вывести закономерности. Свойства параллельных прямых:
Теорема 1. Внутренние накрестлежащие углы равны
Доказательство: Пусть a и b — две параллельные прямые, c — секущая, A и B — точки пересечения секущей с этими прямыми. Пусть утверждение теоремы ложно. Проведем тогда через точку A прямую d, такую что внутренние накрест лежащие углы при прямых b и d и секущей c равны. Тогда по первому признаку параллельности прямых, прямые b и d параллельны. Но прямые b и a параллельны. Значит, через точку A проходят две прямые — a и d, параллельные прямой b. Это противоречит IX аксиоме. Значит, утверждение теоремы верно. Теорема доказана.
Теорема 2. Внешние накрестлежащие углы равны
Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 3. Сумма внутренних односторонних углов равна 180 градусам
Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 4. Сумма внешних односторонних углов равна 180 градусам
Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 5. Соответственные углы равны
Доказательство: Очевидно из первого свойства параллельных прямых.
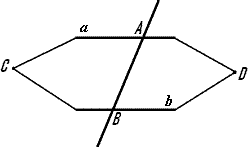
Теорема 6. Если при пересечении двух прямых а и b третей прямой с внутренние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными
Доказательство: Пусть прямые a и b пересекаются секущей в точках A и B, но прямые a и b пересекаются в точке C (рис. 15). Секущая c разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник ABD, равный треугольнику ABC, с вершиной D в другой полуплоскости. Угол DAB равен углу ABC, а значит, точка D лежит на прямой a по условию. Аналогично точка D лежит на прямой b. Следовательно, точка D принадлежит прямым a и b. Значит, прямые a и b пересекаются в двух точках — C и D. Противоречие. Значит, исходное предположение не верно. Теорема доказана.
Теорема 7. Если при пересечении двух прямых а и b третей прямой с внешние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными
Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 8. Если при пересечении двух прямых а и b третей прямой с сумма внутренних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными
Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 9. Если при пересечении двух прямых а и b третей прямой с сумма внешних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными
Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 10. Если при пересечении двух прямых а и b третей прямой с соответственные углы равны (одна пара), то такие прямые а и b являются параллельными
Доказательство: Очевидно из первого признака параллельности прямых.
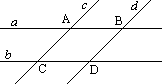
Доказательство: Пусть прямые a и b параллельны прямой c. Допустим, что прямые a и b не па-раллельны. Тогда либо прямые a и b совпадают, что противоречит условию, либо пересекаются в не-которой точке S. Тогда через точку S проходит две прямые — a и b, параллельные прямой c, что противоречит IX аксиоме. Значит, исходное предположение не верно. Теорема доказана.
Теорема 11.1. Если параллельно одной из двух параллельных прямых провести третью прямую, вторая из этих прямых либо параллельна третьей, либо совпадает с ней.
Доказательство: Очевидно из теоремы 11 параллельности прямых.
Теорема 12. Если прямая пересекает одну из параллельных прямых, то она пересекает и вторую.
Теорема 13. Отрезки параллельных прямых, заключенные между некой (иной) парой параллельных прямых, равны.
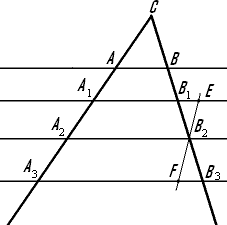
Теорема 14. (Теорема Фалеса) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство: Пусть A1, A2, A3 — точки пересечения параллельных прямых с одной из сторон угла, и точка A2 лежит между точками A1 и A3. Пусть B1, B2, B3 — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A1A2 = A2A3, то B1B2 = B2B3. Проведем через точку B2 прямую EF, параллельную прямой A1A3. Треугольники EB2B1 и FB2B3 равны по второму признаку равенства треугольников. У них стороны EB2 и FA2 равны по условию, углы B1B2E и B3B2F равны как вертикальные, а углы B1EB2 и B2FB3 равны как внутренние накрест лежащие при секущей EF. Значит, B1B2 = B2B3. Что и требовалось доказать.
Теорема 14.1.. Параллельные прямые, пересекая стороны угла, отсекают пропорциональные отрезки.
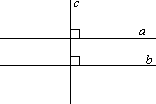
Доказательство: Действительно, внутренние накрест лежащие углы равны 90°. Следовательно, по первому признаку параллельных прямых, эти прямые параллельны.
Теорема 16. Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй.
Доказательство: Очевидно из теоремы 15.
Видео:Перпендикулярные и параллельные прямые. Математика 6 классСкачать

Параллельные прямые
Параллельные прямые . Расстояние между параллельными прямыми .
Углы с соответственно параллельными сторонами .
Соответственные углы .
Внутренние и внешние накрест лежащие углы .
Внутренние и внешние односторонние углы .
Углы с соответственно перпендикулярными сторонами .
Пропорциональные отрезки . Теорема Фалеса.
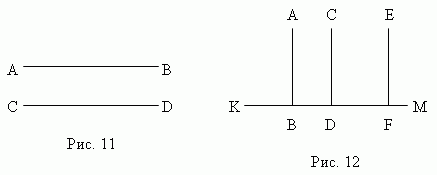
Две прямые AB и CD ( рис.11 ) называются параллельными , если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Обозначение: AB || CD . Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой. Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Угол между двумя параллельными лучами равен нулю, если у них одинаковые направления, и 180 ° , если их направления противоположны. Все перпендикуляры ( AB , CD , EF , рис.12 ) к одной и той же прямой KM параллельны между собой. Обратно, прямая KM , перпендикулярная к одной из параллельных прямых, перпендикулярна и к остальным. Длина отрезка перпендикуляра, заключённого между двумя параллельными прямыми, есть расстояние между ними.
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов ( рис.13 ), которые попарно называются:
1) соответственные углы ( 1 и 5; 2 и 6; 3 и 7; 4 и 8 ); эти углы попарно
равны: (







2) внутренние накрест лежащие углы ( 4 и 5; 3 и 6 ); они попарно равны;
3) внешние накрест лежащие углы ( 1 и 8; 2 и 7 ); они попарно равны;
4) внутренние односторонние углы ( 3 и 5; 4 и 6 ); их сумма равна 180 °
( 



5) внешние односторонние углы ( 1 и 7; 2 и 8 ); их сумма равна 180 °
( 



Углы с соответственно параллельными сторонами либо равны друг другу ( если они оба острые, или оба тупые, 



Углы с соответственно перпендикулярными сторонами также либо равны друг другу ( если они оба острые, или оба тупые ), либо их сумма равна 180 ° .
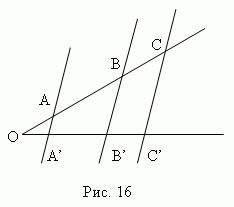
Теорема Фалеса. При пересечении сторон угла параллельными прямыми ( рис.16 ) стороны угла делятся на пропорциональные отрезки:
Copyright © 2004 — 2007 Др. Юрий Беренгард. All rights reserved.
🎬 Видео
Параллельные прямые | Математика | TutorOnlineСкачать

Перпендикулярные прямыеСкачать

Параллельные прямые. 6 класс.Скачать

7 класс, 12 урок, Перпендикулярные прямыеСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Параллельные и перпендикулярные прямые.Скачать

7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Перпендикулярность прямой и плоскости. 10 класс.Скачать

Геометрия 7 класс. Углы с соответственно параллельными или перпендикулярнымСкачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ перпендикулярные к плоскости 10 классСкачать

Перпендикулярность прямых в пространстве. 10 класс.Скачать

Пересекающиеся и параллельные прямые, лучи, отрезки. Задачи. Геометрия. Математика 2 класс.Скачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

№96. Докажите, что отрезки параллельных прямых, заключенные между плоскостью и параллельнойСкачать

16. Параллельные прямые, перпендикулярные к плоскостиСкачать

Тема ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕСкачать