Пересечение окружности с квадратом

Видео:Площадь круга. Математика 6 класс.Скачать

Определение

Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.

На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.

Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Формулы

Радиус вписанной окружности в квадрат

1. Радиус вписанной окружности в квадрат, если известна сторона:
   

Радиус вписанной окружности в квадрат, если известен периметр:

Радиус вписанной окружности в квадрат, если известна площадь:

Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:

Радиус вписанной окружности в квадрат, если известна диагональ:

Радиус описанной окружности около квадрата

1. Радиус описанной окружности около квадрата, если известна сторона:
   

Радиус описанной окружности около квадрата, если известен периметр:

Радиус описанной окружности около квадрата, если известнаплощадь:

Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:

Радиус описанной окружности около квадрата, если известнадиагональ:

Сторона квадрата

1. Сторона квадрата вписанного в окружность, если известнаплощадь:
   

Сторона квадрата вписанного в окружность, если известнадиагональ:

Сторона квадрата вписанного в окружность, если известен периметр:

Площадь квадрата

1. Площадь квадрата вписанного в окружность, если известна сторона:

Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:

Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:

Площадь квадрата вписанного в окружность, если известен периметр:

Площадь квадрата вписанного в окружность, если известна диагональ:

Периметр квадрата

1. Периметр квадрата вписанного в окружность, если известна сторона:
   

Периметр квадрата вписанного в окружность, если известна площадь:

Периметр квадрата вписанного в окружность, если известенрадиус вписанной окружности:

Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:

Периметр квадрата вписанного в окружность, если известна диагональ:

Диагональ квадрата

1. Диагональ квадрата вписанного в окружность, если известна сторона:
   

Диагональ квадрата вписанного в окружность, если известна площадь:

Диагональ квадрата вписанного в окружность, если известен периметр:

Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:

Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:

Видео:Как вписать квадрат в окружностьСкачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:Алгоритмы. Пересечение окружностейСкачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:Как построить квадрат, два способаСкачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:2 круга 1 квадрат ➜ Задача от @AndyMath ➜ Найдите площадь квадрата на рисункеСкачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:16 задание ОГЭ 2023 Окружность Квадрат#ShortsСкачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:Найти площадь пересечения кругов. Задача для тех, кто учился в школе на пятеркиСкачать

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:Квадрат в окружности или окружность в квадрате #ShortsСкачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:Круг внутри квадрата. ищем площадь квадрата, если у круга радиус 7. огэ геометрия задание 17Скачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Лучший способ найти площадь кругаСкачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

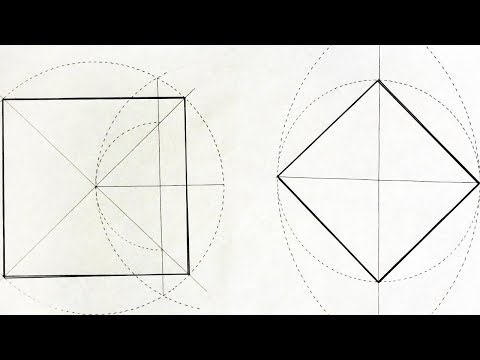
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

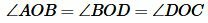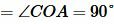(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

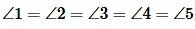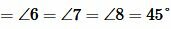(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Видео:Как найти сторону квадрата в который вписаны 2 окружностиСкачать

Как найти количество точек пересечения окружности и квадрата?

Внизу приведена задача, с решением которой возникли трудности.
Как находить кол-во точек пересечения?
Варианты 3,4,7 вызвали трудности.

Даны координаты центра круга и его радиус, а также координаты центра
квадрата и его длина стороны.
Найти взаимное расположение фигур.
Набросок вариантов:
1) Окружность вписана в квадрат
2) Окружность описана вокруг квадрата
3) Окружность и квадрат касаются в одной точке (внешнее и внутреннее
касание)
4) Окружность и квадрат касаются в двух точках
5) Окружность лежит внутри квадрата
6) Квадрат лежит внутри окружности
7) Окружность и квадрат пересекаются в двух и более точках

📸 Видео

Задача С5: пересечение графиков окружности и модуляСкачать

Метод выделения полного квадрата. 8 класс.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Найти площадь квадрата описанного около окружности радиуса 19Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия. ОГЭ по математике. Задание 16Скачать