Единичная окружность самостоятельная работа 10 класс

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Скачать:

Хочешь подготовиться к ЕГЭ за 1450 ₽ в месяц?

Вебинары Учи.Дома помогут подготовиться к ЕГЭ 2022. Поддерживающее коммьюнити из классных преподавателей, которые состоят в комиссии и знают особенности заданий изнутри. Хочешь попробовать бесплатно? Кликай по кнопке!

попробовать бесплатно, онлайн, 40 минут

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Предварительный просмотр:

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) π; б) ; в) ; г) ; д) ; е) .

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) ; е) 3π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с ординатой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с абсциссой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) 3; е) 2π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) 4; е) 10π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) 2π; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) π; б) ; в) ; г) ; д) ; е) .

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) ; е) 3π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с ординатой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с абсциссой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) 3; е) 2π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) 4; е) 10π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) 2π; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) π; б) ; в) ; г) ; д) ; е) .

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) ; е) 3π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с ординатой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с абсциссой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) 3; е) 2π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) ; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

«Числовая окружность. Числовая окружность на координатной плоскости»

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) ; б) ; в) ; г) ; д) 4; е) 10π.

1. По заданному обозначению дуги окружности укажите её геометрическую и аналитическую модели.
2. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты: а) 2π; б) ; в) ; г) .
3. Найдите на числовой окружности точки с абсциссой и запишите, каким числам t они соответствуют.
4. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству , и запишите при помощи двойного неравенства, каким числам t они соответствуют.

Видео:Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать

По теме: методические разработки, презентации и конспекты

Дидактический материал по алгебре и началам анализа в 10 классе (профильный уровень) «Числовая окружность на координатной плоскости»

Вариант 1.1.Найти на числовой окружности точку:А) -2∏/3Б) 72.Како й четверти числовой окружности принадлежит точка 16.3.Найти ко.

Дидактический материал по алгебре и началам анализа в 10 классе (профильный уровень) «Числовая окружность на координатной плоскости»

Вариант 1.1.Найти на числовой окружности точку:А) -2∏/3Б) 72.Како й четверти числовой окружности принадлежит точка 16.3.Найти ко.

Конспект урока алгебры в 10 классе по теме «Числовая окружность на координатной плоскости»

Конспект урока алгебры в 10 классе по теме «Числовая окружность на координатной плоскости» по учебнику автора Мордкович.

Презентация по теме Числовая окружность на координатной плоскости

Родионова Г. М. Числовая окружность на координатной плоскости// Алгебра и начала анализа 10 класс//.Презентация содержит материал : числовая окружность на координатной плоскости, основные .

урок по теме «Числовая окружность на координатной плоскости»

Представлена разработка урока по теме: «Числовая окружность на координатной плоскости» для аудиатории 10 класса.

Числовая окружность в координатной плоскости

Презентация к уроку математики 10 класса: Числовая окружность в координатной плоскости.

Видео:Тригонометрическая окружность. Как выучить?Скачать

ГДЗ Алгебра Самостоятельные работы за 10 класс Александрова Базовый уровень Мнемозина (к учебнику Мордкович)

Алгебра в 10 классе имеет свои трудности, которые он должен преодолеть как можно скорее. Эти проблемы касаются не только правил, формул, но и умения мыслить и понимать задачи. А это умение, как известно, является одной из самых сложных способностей человека. Выполнение самостоятельной работы по алгебре ставит перед десятиклассником ряд личностно – значимых проблем, которые позволяют понять самому, как решать задачи. Это не просто подготовка к работе на уроке по шаблону, но и самостоятельное создание ситуации успеха, которая должна стать нормой для каждого ученика. Только в этом случае, любой десятиклассник сможет найти возможность проявить свои способности, почувствовать, что он чего – то может достичь самостоятельно. Проверить правильность выполненных решений можно с помощью ГДЗ по алгебре и начала математического анализа Александрова Л.А., которое полностью соответствует всем требованиям школьной программы основного среднего образования и федеральному государственному общеобразовательному стандарту.

Сформировать умения применять свои знания на практике в различных ситуациях и разных предметных областях является одной из главных задач обучения. Освоение знаний – это только половина дела. Главное это иметь большое желание учиться, быть любознательным, а так же уметь добывать эти знания, пользоваться ими в определенной ситуации, такого требования общеобразовательного стандарта.

Одной из основных причин неспособность школьника применять математические знания в практической работе является отсутствие или недостаток знаний об общих закономерностях, умение осуществлять выбор способа решения в конкретной ситуации, а так же и опыта применения математики для решения задач в смежных предметах. Овладеть школьником методов решения задач повышает его уровень математического развития. Математический язык относится к числу наиболее распространенных языков. Он широко используется в литературе, в печати, в научно – технических и практических публикациях. Благодаря этому и язык математики получил широкое применение в других научных дисциплинах. Язык математики имеет свои законы развития, что объясняется её природой. В языке математики можно выделить две основные составляющие: – это естественный язык (его ещё называют языком логики), на котором принято выражать мысли, и символы, которыми изображаются эти мысли. Именно при обучении алгебры в школе ставится задача овладеть символьным языком алгебры, это и позволит ученику глубже разобраться в математических моделях, что в свою очередь позволит в дальнейшем более полно использовать математический аппарат в экономических расчетах. Для этого в качестве объектов исследования были выбраны некоторые элементы математического аппарата алгебры, такие как определители, матрица, вектор, операции, сложение и так далее. Необходимость изучения комплекс чисел в курсе алгебры и начала математического анализа обуславливается потребностью в математических моделях многих физических явлений. В настоящее время одним из основных направлений развития теории дифференциальных уравнений является её приложение к задачам механики сплошных сред. Это направление связано с созданием теории одномерных и двумерных уравнений математической физики, где на первый план выходят задачи о фазовых переходах. Для решения таких задач необходимо знание свойств интегральных представлений функции, имеющие множество точек разрыва.

Видео:Тригонометрические функции одного и того же угла В2Скачать

ГДЗ по алгебре Самостоятельные работы за 10 класс Александрова Базовый уровень к учебнику Мордкович

Курс алгебры и начала математического анализа является основой для получения фундаментальных знаний в областях, непосредственно примыкающих к школьной программе и для продолжения образования в технических, экономических и гуманитарных в высших учебных заведениях. К тому же курс алгебры и начала математического анализа является завершающим этапом в школьном обучении математики. Этот курс имеет большую практическую значимость, что связано с формированием и развитием ряда умений и навыков. При изучении этой дисциплины у десятиклассника вырабатываются навыки работы с тестовыми заданиями. Ученик учится самостоятельно работать, наблюдать, обобщать, делать выводы, применять теоретические знания на практике. Умения и навыки формируются в процессе решения примеров и задач. Для этого отлично подойдет использование ГДЗ по алгебре и начала математического анализа 10 класс Александрова Л.А., который поможет глубже вникнуть в систему понятий, необходимых для решения задач, входящих в школьный курс элементарной математики. В нем отражены все темы учебника такие как:

• числовые функции,
• тригонометрические функции и уравнения,
• преобразование тригонометрических выражений,
• производная.

Решебник является можно сказать, что по сути своей он выполняет функции репетитора по алгебре. Он содержит в себе не только решения простых примеров и задач, но и более сложных. Пользоваться онлайн – решебником можно в любое, удобное для школьника, время и в любом месте, где имеется выход в Интернет, хоть с компьютера, хоть с любого электронного устройства. С его помощью каждый ученик сможет:

• получить полное качественное выполнение домашнего задания,
• провести подготовку, как к самостоятельной работе, так и подготовку к следующему уроку,
• устранить имеющиеся пробелы в знании той или иной темы,
• закрепить знания.

Решебник поможет и родителям проверить, насколько их ребенок знает алгебру.

Его может использовать и учитель математики для проверки домашнего задания, подготовке к самостоятельной работе, а так же как справочное пособие.

Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Дидактический материал по теме «Тригонометрия»

Самостоятельные работы и тест по теме «Тригонометрия»

Содержимое разработки

Государственное учреждение образования

«Средняя школа № 17 г. Могилева»

I квалификационной категории

Мог и лев 2016 г.

Градусная и радианная мера произвольных углов

Определение синуса, косинуса, тангенса и котангенса произвольного угла

Найдите координаты точки, полученной поворотом точки Р (1;0) на угол — .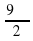

Отметьте на единичной окружности точку А_α, если:

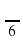
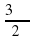
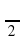
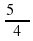
а) α =; б) α = ; в) α = 567 0 ; г) α = — ; д) α = ; е) α = — 1230 0 .

В какой четверти координатной плоскости расположена точка А_α, если α равно:

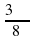
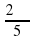
а) ; б) — ; в) 830 0 ; г) -1250 0 ; д) 1,8π; е) -2,3π.

На единичной окружности отметьте точку А_α (х; у), координаты которой удовлетворяют условию:

а) у = 0,5, х 0; б) х = 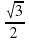, у 0.

Укажите три значения градусной меры угла α, при которых абсцисса соответствующей ему точки А_α равна:

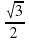
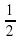
а) ; б) – 1; в) 0; г) — .

Градусная и радианная мера произвольных углов

Выразите в радианной мере величины углов:

а) 36 0 ; б) 216 0 ; в) 310 0 ; г) 360 0 ; д) 1021 0 .

Выразите в градусной мере величины углов:

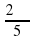
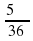
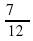
а) ; б) ; в) 5,3; г) — ; д) 11.

Определите в какой четверти оканчивается угол α, если его радианная мера равна:

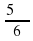
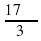
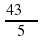
а) 9,1π; б) ; в) — ; г) -6,3π; д) — .

С помощью калькулятора или таблиц найдите:

а) радианные меры углов 17 0 ; 43 0 24 ‘ ; 83 0 36 ‘ ; 72 0 12 ‘ ;

б) градусные меры углов 0,384; 0,48; 1,11; 1,48.

а) Найдите радианную меру центрального угла сектора, если длина соответствующей дуги равна диаметру круга.

б) Длина дуги сектора втрое меньше его периметра. Найдите радианную меру его центрального угла.

Определение синуса, косинуса, тангенса и котангенса произвольного угла

Могут ли синус и косинус одного и того же угла быть равными соответственно:

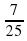
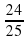
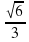
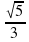
а) — и ; б) 0,4 и 0,7; в) и — .

Найдите числовое значение выражения:

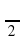
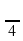
а ) sin 0 + cos + sin 2 ;

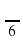
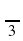
б ) 6 sin — 2 cos 0 + tg 2 ;

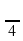
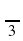
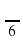
в ) 3 tg — sin 2 + cos 2 .

Отрицательным числом является:

а) cos 1300 0 ∙ sin 930 0 ∙ tg 185 0 ;

б ) cos 1230 0 ∙ sin 490 0 ∙ ctg 125 0 ;

в ) cos 1336 0 ∙ sin 691 0 ∙ tg 250 0 ;

г) cos 3600 0 ∙ sin 1290 0 ∙ ctg 250 0 .

Найдите значение выражения:

.

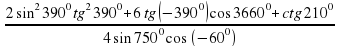
🔥 Видео

Числовая окружность | Алгебра 10 класс #8 | ИнфоурокСкачать

Тригонометрия. 10 класс. Вебинар | МатематикаСкачать

Единичная окружность. Градусная и радианная меры произвольного угла. Вариант 1Скачать

самостоятельная работа 3. 10 классСкачать

1. Числовая окружность. 10 классСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Формулы приведения - как их легко выучить!Скачать

Как искать точки на тригонометрической окружности.Скачать

Контрольная работа 1Скачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Алгебра. 10 класс. Самостоятельные и контрольные работыСкачать

Тема 1. Единичная окружность. Градусная и радианная мера произвольного угла. Определение синуса и тдСкачать