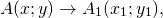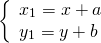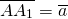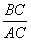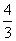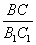Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса

то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
- Планиметрия. Страница 7
- 1.Движение и его свойства
- Свойства движения
- 2.Симметрия относительно точки
- 3.Симметрия относительно прямой
- 4.Параллельный перенос и его свойства
- Свойства параллельного переноса
- Репетитор: Васильев Алексей Александрович
- 5.Пример 1
- Пример 2
- Пример 3
- Пример 4
- Пример 5
- Параллельный перенос, поворот плоскости и подобные треугольники
- Корзина
- Параллельный перенос
- Поворот плоскости вокруг точки на угол
- Подобные треугольники
- 🎬 Видео
Видео:9 класс, 32 урок, Параллельный переносСкачать

Планиметрия. Страница 7

Видео:Перенос треугольника по векторуСкачать
1.Движение и его свойства
Пусть на плоскости задана геометрическая фигура. Если каждую точку данной фигуры переместить на некоторое расстояние, так чтобы расстояние между точками сохранилось, то мы получим новую фигуру, преобразованную из данной. (Рис.1) Таким образом, преобразование одной фигуры в другую так, что расстояние между точками остается неизменным, называется движением.
Например, при перемещении фигуры М на некоторое расстояние получим фигуру М1. Все точки фигуры М передут в точки фигуры М1. Расстояние между точками сохранится АВ = А1В1
Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Свойства движения
При движение все точки, лежащие на прямой, перейдут в точки также лежащие на прямой. Порядок их взаимного расположения останется неизменным. Т.е. Прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки и т.д. При движении градусная мера угла между двумя полупрямыми останется неизменной.

Рис.1 Движение и его свойства.
Видео:Угол между векторами. 9 класс.Скачать

2.Симметрия относительно точки
Пусть на плоскости задана точка О. (Рис.2) Возьмем произвольную точку А. Если через точки О и А провести прямую и отложить от точки О отрезок ОА’, равный отрезку АО, то точка О будет называться точкой симметрии. А точка А’ — точкой симметричной точке А относительно точки О.
При преобразовании фигур каждая точка переходит в симметричную ей точку относительно точки симметрии О. Такое преобразование называется преобразованием симметрии, а фигуры называются симметричными относительно точки О.
Если при преобразовании фигура переходит в саму себя, то она называется центрально-симметричной, а точка О называется точкой симметрии. Например, параллелограмм, окружность, эллипс, ромб, квадрат.
Преобразование фигур относительно точки симметрии является движением.
Рис.2 Симметрия относительно точки.
Видео:Координаты вектора. 9 класс.Скачать

3.Симметрия относительно прямой
Пусть дана прямая а. (Рис.3). Если взять произвольную точку, например точку Е, провести перпендикуляр к прямой а и на продолжении этого перпендикуляра отложить отрезок ВE’, равный отрезку ЕВ, то точка Е’ будет симметрична относительно прямой а. Если точка лежит на прямой а, то она симметрична сама себе.
При преобразовании фигуры в фигуру каждая точка переходит в точку С’, симметричную относительно прямой а. Такое преобразование называется преобразование симметрии относительно прямой.
Преобразование симметрии относительно прямой также является движением, т.к. согласно определению движения расстояние между точками фигуры при смещении относительно прямой не изменяется.

Рис.3 Симметрия относительно прямой.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

4.Параллельный перенос и его свойства
Пусть на плоскости с осями координат Ox и Oy задана фигура S. Каждая точка фигуры параллельным переносом переходит в точку А’ на одно и тоже расстояние. Тогда можно дать следующее определение: преобразование фигуры S в фигуру S’, в котором каждая точка фигуры с координатами x и y смещается в точку с координатами x+a и y+b, где a и b постоянные числа, называется параллельным переносом.
Параллельный перенос есть движение, т.к. все точки смещаются на одно и тоже расстояние.
Таким образом, для получения координат новой фигуры, параллельный перенос задается следующими формулами:
x’ = x + a
y’ = y + b
Видео:11 класс, 12 урок, Параллельный переносСкачать

Свойства параллельного переноса
При параллельном переносе все точки какой-либо фигуры смещаются по параллельным прямым на одно и тоже расстояние. Перпендикулярные прямые переходят в перпендикулярные прямые, параллельные прямые — в параллельные. Расстояния между точками какой-либо фигуры при перемещении, так же как и углы между прямыми, сохраняются.

Рис.4 Параллельный перенос и его свойства.
Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

5.Пример 1
Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии.
Доказательство:
Пусть дан параллелограмм АВA’В’ (Рис.5). По свойству параллелограмма, его диагонали делятся точкой пересечения пополам, а противолежащие стороны параллельны и равны. Следовательно, треугольники АОB’ и ВОА’ равны по двум сторонам и углу между ними. АО = ОА’, ВО = ОB’, углы при вершине О равны как вертикальные. А отсюда следует, что точки A’ и B’ симметричны точкам А и В относительно точки О. Т.е. получается, что вершины параллелограмма центрально симметричны относительно точки О.
Теперь на стороне АВ’ возьмем произвольную точку Е и проведем через нее прямую, проходящую через точку О. Треугольники ЕОВ’ и BOE’ равны по второму признаку равенства треугольников: по стороне и прилегающим к ней углам. BO = OB’ и углы при вершинах О и В,B’ равны (при вершине О как вертикальные, при вершинах B,B’ как внутренние накрест лежащие). Следовательно, отрезки ЕО и ОE’ равны, т.е. ЕО = ОE’.
Рис.5 Задача. Докажите, что у параллелограмма.
Отсюда можно сделать вывод, что каждая точка Х параллелограмма переходит в точку X’, симметричную относительно данной точки О. Т.е. преобразование симметрии относительно точки О переводит параллелограмм в сам себя, поэтому он называется центрально-симметричной фигурой, а точка О является его центром симметрии.
Пример 2
Докажите, что прямая, содержащая медиану равнобедренного треугольника, которая проведена к основанию, является его осью симметрии.
Доказательство:
Пусть АВА’ данный равнобедренный треугольник с основанием АА’, АВ = ВA’ (Рис.6). Медиана ОВ лежит на прямой а. Так как медиана делит противолежащую сторону пополам, то треугольники АВО и A’BO равны по трем сторонам (АВ = ВA’, АО = ОA’, сторона ОВ у них общая). Следовательно, углы при вершине О равны 90°, как равные смежные углы. А углы при вершине В равны, так как треугольники равны. Следовательно, вершина треугольника А симметрична вершине A’ относительно прямой а, так как основание АA’ перпендикулярно прямой а. Так же как и для любой точки, принадлежащей отрезку АО, найдется симметричная ей точка на отрезке ОА’ относительно прямой а.
Точка В лежит на прямой а, поэтому она симметрична сама себе относительно прямой а.
Теперь проведем произвольную прямую b, параллельную основанию АА’. Она пересечет боковые стороны треугольника в точках ЕЕ’. Рассмотрим треугольники ЕВО’ и BO’E’. Они равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам: сторона BO’ у них общая, углы при вершинах В и О’ равны). Следовательно, ЕО’ = O’E’.
Рис.6 Задача. Докажите, что прямая, содержащая медиану.
Отсюда следует, что любая точка Х’ треугольника ВОА’ симметрична точке Х треугольника АВО относительно прямой а, что является преобразованием симметрии относительно прямой. А если преобразование симметрии относительно прямой а переводит треугольник АВА’ сам в себя, то прямая а является его осью симметрии.
Пример 3
Параллельный перенос задается формулами x’ = x + 2, y’ = y — 3. В какие точки при этом параллельном переносе переходят точки А (1;1), В (2;2), С (-2;0).
Решение:
По условию задачи параллельный перенос задается формулами:
x’ = x + 2, y’ = y — 3
Следовательно, точка А переходит в точку А’ с координатами:
x’ = 1 + 2 = 3, y’ = 1 — 3 = -2, т.е. A’ (3;-2).
Точка В переходит в точку В’ с координатами:
x’ = 2 + 2 = 4, y’ = 2 — 3 = -1, т.е. В’ (4;-1).
Точка С переходит в точку С’ с координатами:
x’ = -2 + 2 = 0, y’ = 0 — 3 = -3, т.е. С’ (0;-3). (Рис.7)
Рис.7 Задача. Параллельный перенос задается формулами.
Пример 4
Докажите, что если у двух ромбов равны диагонали, то они равны.
Доказательство:
Пусть даны два ромба: ABCD и A»B»С»D». AC = A»C», BD = B»D». Углы между диагоналями равны 90°. Докажем, что они совмещаются движением, причем вершина А переходит в вершину A», вершина В — в B», вершина С — в С», вершина D — в D».
Подвергнем ромб ABCD преобразованию симметрии относительно прямой а, перпендикулярной отрезку СС’ и проходящей через его середину (Рис.8). Если два ромба не располагаются друг под другом, то нужного расположения можно добиться при помощи параллельного переноса. (Напомним, что параллельный перенос также является движением со всеми вытекающими из этого свойствами.) В результате получим ромб A’B’C’D’. Если точки А и А’ различны, то подвергнем его симметрии относительно прямой b, перпндикулярной отрезку A’A» и проходящей через его середину и точку С’. Таким образом, отрезок A’C’ перейдет в отрезок A»C». И в результате получим ромб A»B»’C»D»’.
Преобразование симметрии относительно прямой является движением. А при движении точки переходят в точки, прямые — в прямые, углы между прямыми, так же как и расстояния между точками, сохраняются.
Рис.8 Задача. Докажите, что если у двух ромбов.
Отсюда следует, что отрезок B»’D»’ перпендикулярен отрезку А»C» и проходит через его середину, а точки B»’ и D»’ совпадают с точками B» и D», так как по условию задачи диагонали двух ромбов равны. Таким образом, получается, что диагонали ромба АС и BD полностью совпадут с диагоналями A»C» и B»D». А из этого следует, что и вершины ромба ABCD полностью совпадут с вершинами ромба A»B»C»D», так как они находятся на концах диагоналей. Следовательно, ромб ABCD полностью перейдет в ромб A»B»C»D».
Пример 5
Существует ли параллельный перенос, при котором точка А (2;2) переходит в точку A'(3;-2), а точка В (-2;1) переходит в точку В'(-2;-3).
Решение:
Параллельный перенос задается формулами:
x’ = x + a, y’ = y + b
где а и b одни и те же числа. Отсюда следует, что
a = x’ — x, b = y’ — y. Подставим координаты точки А и A’:
a = 3 — 2, b = -2 — 2; т.е. a = 1, b = -4
Следовательно, параллельный перенос по точке А задается формулами: x’ = x + 1, y’ = y — 4
Отсюда, координаты точки В» будут:
x» = -2 + 1 = -1, y» = 1 — 4 = -3
т.е. B»(-1;-3), а точка B’ имеет координаты (-2;-3).
Следовательно, такого параллельного переноса не существует. (Рис.9)
Рис.9 Задача. Существует ли параллельный перенос.
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Параллельный перенос, поворот плоскости и подобные треугольники
Корзина

Теоретический урок по предмету математики для решения задач по теме «Параллельный перенос, поворот плоскости и подобные треугольники».
Содержание данной онлайн страницы электронного справочника для школьников:
- – тема «Параллельный перенос» представлена на примере решения задач 145 — 148;
- – в контрольных работах с номерами 149 — 154 данной рабочей тетради по математике рассматривается поворот плоскости вокруг точки на угол;
- – повторение курса геометрии 9 класса в решениях приведено на примере заданий 155 — 173: углы треугольника, площадь треугольника через катеты и гипотенузу, вычисление радиуса описанной окружности, стороны ромба, подобные треугольники.
Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

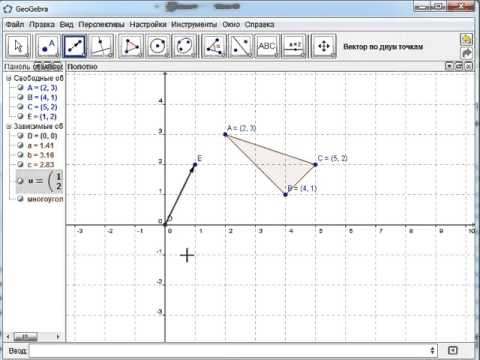
Параллельный перенос


Параллельным переносом на вектор 


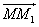

Задача 145.



A → A1 : 


B → B1 : 


Теорема:
При параллельном переносе на вектор 

f – параллельный перенос на вектор 
M 

N 



Точка M переводится движением в точку M1 с условием, что два вектора равны: M 



Точка N переводится движением в точку N1 с условием, что два вектора равны: N 



Следовательно, полученные отрезки параллельны MM1 || NN1 и построенные отрезки равны MM1 = NN1
Значит, четырехугольник MM1N1N – параллелограмм.
Поэтому MN = M1N1, значит f – движение.

Задача 146.
A 




B 




C 


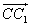


A 




B 




C 


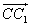



Задача 147.
точка D лежит на AC: D 
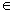
точка C лежит на AD: C 
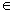
BC 
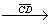
б) Доказать: ABB1D – равнобедренная трапеция
1) От точки B проведем прямую a, параллельную вектору 
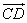

2) Точка B переводится движением в точку B1



3) Проведем прямую B1D, параллельную отрезку BC:
Рассмотрим четырехугольник BB1DC.
Т.к. основания BB1 || CD и боковые стороны BC || BD параллельны, то BB1DC – параллелограмм (по определению)
По свойству параллелограмма:
основания BB1 = CD и боковые стороны BC = BD равны, но AB = BC, тогда AB = B1D
Т.к. BB1 || AD параллельны и AB 
Т.к. AB = B1D, то ABB1D – равнобедренная трапеция.
Задача 148.
Дано: 
вектор 
окр (O;R) 

ΔABC 

EFPQ 

как показано на рисунке.
Видео:Параллельный переносСкачать

Поворот плоскости вокруг точки на угол
Определение:




O – центр поворота
α – угол поворота
Задача 149.


α = 75° (против часовой стрелки)
O – центр поворота
1) A 
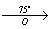


2) B 
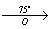


Теорема:
Поворот является движением.


α – угол поворота (против часовой стрелки)
точка O – центр поворота
Тогда треугольники равны ΔOMN = ΔOM1N1 по двум сторонам и углу между ними:




Тогда MN = M1N1, значит, f – движение.
Задача 150.
точка O – центр поворота


1) A 
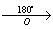


2) B 
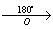


Задача 151.
точка A – центр поворота
α = 160° (против часовой стрелки)
1) B 
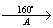


2) C 


Задача 152.
точка O – центр поворота


1) A 


2) B 


Задача 153.
точка C – центр окружности (C; R)
точка O – центр поворота
угол поворота α = 60° (против часовой стрелки)
а) точка C и точка O не совпадают
б) точка C и точка O совпадают


1) проведем луч CO
2) C 



Т.к. точка О – центр поворота и точка С – центр окружности совпадают, то окружности (C;R) и (C1;R) будут тоже совпадать.

Задача 154.
Δ ABC – равнобедренный, равносторонний
D – точка пересечения биссектрис
D – центр поворота
угол поворота α = 120°
ΔABC 

Т.к. Δ ABC – правильный, то все углы в нем равны 60°.
Т.к. точка D – центр описанной и вписанной окружности, то
Δ ABD = Δ BDC = Δ DAC (по трем сторонам).
Следовательно, что 





A 

B 

C 

Таким образом, Δ ABC отображается на себя.
Повторение.
Задача 155.






Найти: наибольший угол треугольника
Пусть x – коэффициент пропорциональности. Зная, что сумма углов в треугольнике равна 180°, составим и решим уравнение:
3x + 7x + 8x = 180
Наибольший угол 

Задача 156.
треугольник ΔABC – равнобедренный,
один угол больше другого:






Найти: угол при основании треугольника
Пусть x° – угол при основании треугольника. Зная, что сумма углов в треугольнике составляет 180°, составим и решим уравнение:
(x + 60°) + x + x = 180°
Значит, 

Задача 157.
треугольник ΔABC – прямоугольный
c = 26 см – гипотенуза
Найти: больший катет b
Пусть x – коэффициент пропорциональности. По теореме Пифагора составим и решим уравнение:
(5x) 2 + (12x) 2 = 26 2
25x 2 + 144x 2 = 676
b = 12 • 2 = 24 (см)
Задача 158.


c = 13 – гипотенуза
По теореме Пифагора получаем:
a = 
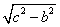

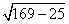

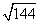
Тогда площадь треугольника
SΔABC = 


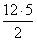
= 30 (квадратных единиц)
Задача 159.
треугольник ΔABC – равнобедренный,


c = 4 
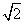
Найти: площадь треугольника SΔABC = ?
SΔABC = 

Т.к. Δ ABC – равнобедренный, то углы при основании по 45° и катеты равны a = b.
По теореме Пифагора получаем:
Тогда (4 
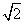
Тогда площадь треугольника
SΔABC = 


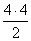
= 8 (квадратных единиц)
Задача 160.




Найти: радиус описанной окружности R = ?
Т.к. AH – медиана, то CH = 

По теореме Пифагора получаем:
Тогда CH = 


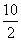
Точка H – центр описанной окружности
Т.к. R = AH, то R = AH = CH = 5 ед.
Задача 161.


соотношение острых углов




AC = 4 
Найти: радиус описанной окружности R = ?


Тогда 



Следовательно, BC = 

По теореме Пифагора получаем:
AC 2 + 
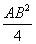
AC 2 = 

AB 2 = 
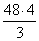
R = AD = BD = 8 : 2 = 4 (ед)
Задача 162.




радиус описанной окружности
Тогда AB = 2,5 • 2 = 5
По теореме Пифагора получаем:
AC = 
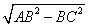

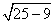

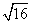




tg 


0,6 = 
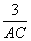

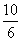
Задача 164.


Найти: 



Т.к. AH = AC, то Δ AHC – равнобедренный.
Точка H – радиус вписанной окружности, поэтому AH = CH, но AH = AC, следовательно, AH = CH = AC.
Тогда Δ AHC – равносторонний.
Значит, 





Задача 165.
треугольник Δ ABC – правильный, равносторонний,
SΔABC = 
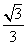
Найти: длину биссектрисы BH = ?


Рассмотрим Δ ABC – равнобедренный, где




Тогда BH – медиана, высота.
Значит, перпендикулярны отрезки BH 
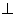
Рассмотрим треугольники Δ ABH и Δ BHC.
AB = BC, по условию.
AH = CH, BH – медиана.
Значит, треугольники равны Δ ABH = Δ BHC.
Т.е. SΔABH = 




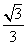

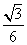
SΔABH = 

Рассмотрим треугольник Δ ABH.
Т.к. BH – биссектриса, то угол 

AH = 

SΔABH = 


AB • BH = 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
AB 2 = 

BH 2 = 

BH = 
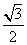
Используя результат (**) в уравнении (*), получаем
AB • 
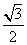

AB 2 = 
AB = 
Тогда AB • BH = 






Задача 166.
треугольник Δ ABC – правильный, равносторонний,


R = 
Найти: площадь треугольника
Рассмотрим Δ ABO (AO = BO = R) 

Проведем из вершины O к AB высоту OH.
Рассмотрим Δ AOH, где 

Т.к. 







OH = 


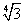

По теореме Пифагора получаем:
OH 2 + AH 2 = OA 2

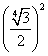

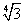



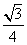
= 
AH 2 = 
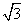

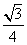

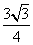



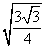

Тогда площадь треугольника
SΔAOH = 




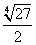

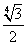

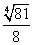

Следовательно, SΔABO = 2 • SΔAOH = 2 • 
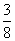


Тогда площадь треугольника
SΔABC = 3 • SΔABO = 3 • 


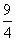




Площадь ромба SABCD = 384
Соотношение диагоналей ромба:
Найти: сторону ромба AB = ?
SABCD = 

Пусть x – коэффициент пропорциональности. Тогда
SABCD = 

Следовательно, диагональ BD = 4x = 4 • 8 = 32
AC = 3x = 3 • 8 = 24
Поэтому половина диагонали AO = 



BO = 



По теореме Пифагора получаем:
AO 2 + BO 2 = AB 2
Сторона ромба AB = 
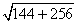

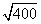
Задача 168.
треугольник Δ ABD – равнобедренный,


Найти: площадь треугольника
SΔABD = 

Проведем высоту BH к основанию AD.
По свойству равнобедренного треугольника:
BH – медиана, биссектриса, высота.
Т.к. BH – медиана, то AH = DH = 16 : 2 = 8 (ед.)
Рассмотрим треугольник Δ ABH, где угол 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
BH = 
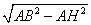

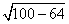

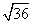
Тогда площадь треугольника
SΔABD = 



Ответ: площадь треугольника SΔABD = 48 кв.ед.

Задача 169.
треугольник Δ ABC –равнобедренный,
основание AC больше высоты BH на 15: AC > BH на 15
Найти: основание AC = ?
Т.к. треугольник Δ ABC –равнобедренный, то BH – высота, медиана, биссектриса.
Тогда AC = AH + CH = AH + AH = 2 AH
Рассмотрим Δ ABH – прямоугольный.
Пусть AC = (x) ед. 


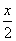
Тогда AB = (x – 15) ед. (по условию).
По теореме Пифагора решим уравнение:
(x – 15) 2 = ( 
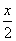



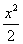
4 (x 2 – 30x) = x 2
4x 2 – 120x = x 2
3x 2 – 120x = 0 | : x
Таким образом, 40 ед. – длина основания.
Ответ: AC = 40 ед.
Видео:Определение преобразований | Геометрические преобразования и Конгруэнтность | ГеометрияСкачать

Подобные треугольники
Задача 170.






CH – биссектриса угла 

Доказать: подобие треугольников
Δ BHC 









Т.к. CH – биссектриса угла 





Рассмотрим Δ BHC








Тогда 



Поэтому треугольники подобны Δ BHC 



верхнее основание BC = 4 см
нижнее основание AD = 10 см
диагональ BD = 8 см
часть диагонали BO = ?
соотношение периметров треугольников


Углы равны 



Углы равны 



Тогда треугольники подобны Δ BCO 




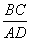

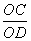







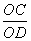













Пусть BO = x, AO = 8 – x. Тогда 10x = 4 • (8 – x)
x = 2 

Следовательно, BO = 2 



Ответ: BO = 2 



Задача 172.
ΔABC 



P (ΔABC) = 12 +16 + 20 = 48 (дм)
Т.к. треугольники подобны, то

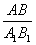

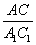




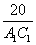


Тогда соотношение периметров треугольников

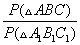
Из равенств (*) и (**) следует



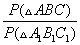




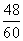

B1C1 = 
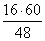
Тогда 





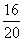



A1B1 = 
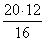
Задача 173.


стороны трапеции пересекаются в точке M:
Рассмотрим треугольники ΔAMD и ΔBMC:








Тогда, по первому признаку подобия треугольников:
треугольники подобны Δ AMD 


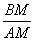

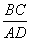

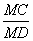


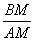

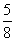
но AM = AB + BM = 3,9 + BM
8 • BM = 5 (3,9 + BM)

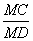

🎬 Видео
Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Скалярное произведение векторов. 9 класс.Скачать

Параллельный перенос точки, отрезка, треугольника, четырехугольника. Геометрия 8 классСкачать

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ПОВОРОТ 9 класс геометрия АтанасянСкачать

Урок 8. Параллельный перенос. Декартовы координаты на плоскости.Скачать

Геометрия и группы. Алексей Савватеев. Лекция 2.3. Параллельный переносСкачать

Геометрия 9 класс : Параллельный перенос и поворотСкачать

Сложение векторов. Правило параллелограмма. 9 класс.Скачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать