- 25 мозговых дразнилок, которые одурачат не только ваши глаза, но и мозги
- Что вы увидели первым на этом рисунке?
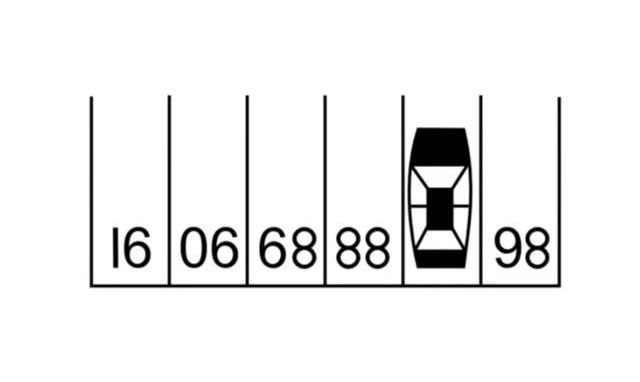
- На каком номере припарковалась машина?
- Загадка
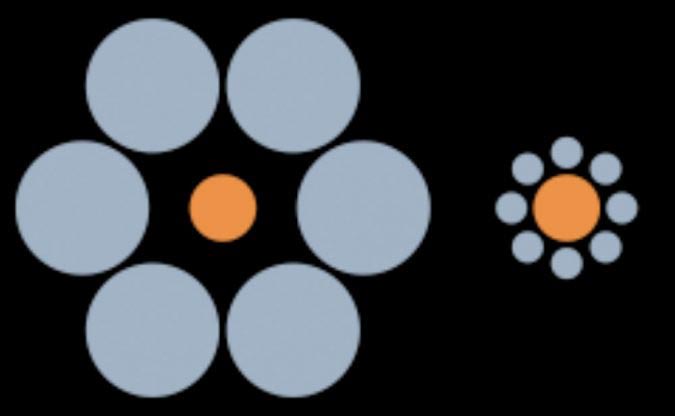
- Оранжевые круги разного размера?
- Загадка: Выберите дверь!
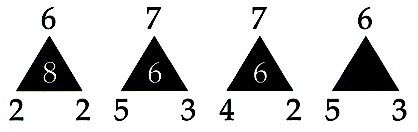
- Какая цифра должна быть в чёрном треугольнике?
- Эти круги статичные, или двигаются?
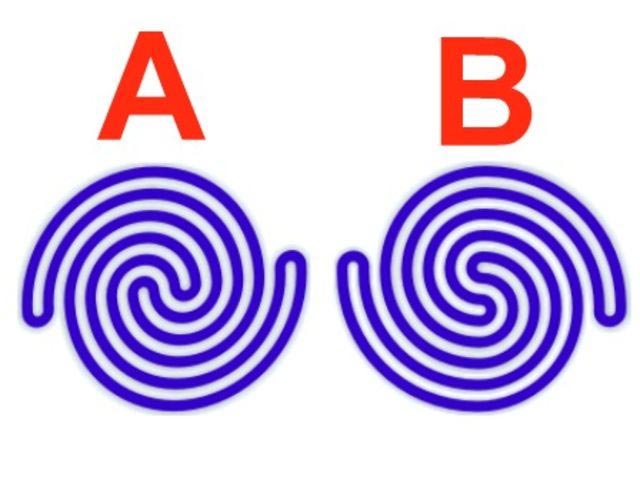
- Какая из этих спиралей образована одним сплошным куском верёвки?
- В какую сторону крутится девушка?
- Поместите рыбку в аквариум
- Эти горизонтальные линии прямые или кривые?
- Сколько ног у слона?
- Загадка
- Квадраты внутри синих и желтых квадратов одного цвета?
- Ровный ли круг внутри большого круга?
- В какую сторону едет автобус?
- Какой из этих квадратов темнее: А или В?
- Загадка: положи меня на одну из моих сторон, и я всё. Сложи меня пополам, и я ничто. Что я?
- Это перевёрнутое лицо Линкольна вам кажется нормальным?
- Видите черные круги на пересечении белых линий?
- Сколько квадратов на этой картинке?
- Горизонтальные линии разной длины?
- Последняя загадка
- Головоломка Волшебный треугольник
- Вам понадобится
- Цель игры
- Задачка на сообразительность: откуда появился лишний пустой квадрат?
- ЗАДАЧА, КОТОРУЮ МОЖЕТ РЕШИТЬ ТОЛЬКО 22% ЛЮДЕЙ
- Перед вами два треугольника
- Ответ:
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

25 мозговых дразнилок, которые одурачат не только ваши глаза, но и мозги
Видео:Из 6-ти спичек выложить 4 равных треугольника 🧐Скачать

Что вы увидели первым на этом рисунке?
Но что более важно, заметили ли вы в ней ребёнка?
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

На каком номере припарковалась машина?
Подсказка: попробуйте взглянуть на задачу со всех сторон.
Ответ: 87 — потому что вы просто смотрите на перевёрнутую картинку
Видео:9 класс, 15 урок, Решение треугольниковСкачать

Загадка
Вы в тёмной комнате со свечой, дровяной печью и керосиновой лампой. У вас только одна спичка. Что вы зажжёте первым?
Ответ: спичку!
Видео:Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

Оранжевые круги разного размера?
Нет! На самом деле они одинаковые
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Загадка: Выберите дверь!
Вы выбегаете из лабиринта, перед вами три двери. Дверь слева ведёт к пылающему аду. Центральная дверь ведёт к кровавому убийце. Дверь справа — ко льву, который не ел три месяца. Какую дверь выберете?
Ответ: лев не смог бы выжить после трёх месяцев голодовки. Третья дверь безусловно самая безопасная.
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Какая цифра должна быть в чёрном треугольнике?
Ответ: шаблон для каждого треугольника выглядит следующим образом: берёте верхнее число, вычитаете из него нижнее левое и умножаете ответ на цифру в нижнем правом углу.
В случае с последним треугольником — это число 3.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Эти круги статичные, или двигаются?
Если водить по изображению глазами, то они кажутся движущимися, но на самом деле они статичные.
Видео:У Мигеля истерика 😅 #shorts #тнт #юмор #мигель #камедибатлСкачать

Какая из этих спиралей образована одним сплошным куском верёвки?
Ответ: А. Это легко проверить проследив за линиями спиралей (ну или просто взглянув в центр).
Видео:Раз ковбой, два ковбой... Рисованный мультфильм (1981)Скачать

В какую сторону крутится девушка?
Бесконечно бородатая гифка, но феномен вращающейся девушки не может не удивлять.
Правильного ответа здесь нет, в этом и есть смысл оптической иллюзии, поэтому иногда вы видите как девушка крутится по часовой стрелке, а иногда против.
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

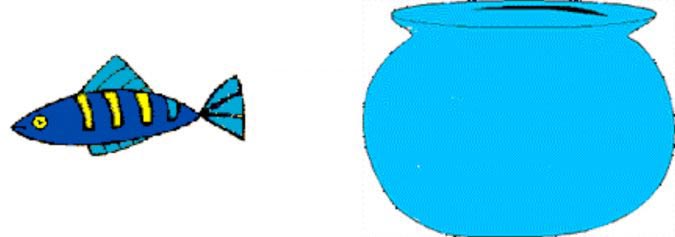
Поместите рыбку в аквариум
Смотрите на центральную жёлтую полоску рыбки в течение примерно 10 секунд, а затем быстро посмотрите на аквариум и поморгайте.
Заметили очертание рыбки с инвертированными цветами?
Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Эти горизонтальные линии прямые или кривые?
Эти линии прямые, даже если они такими не выглядят.
Видео:№547. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.Скачать
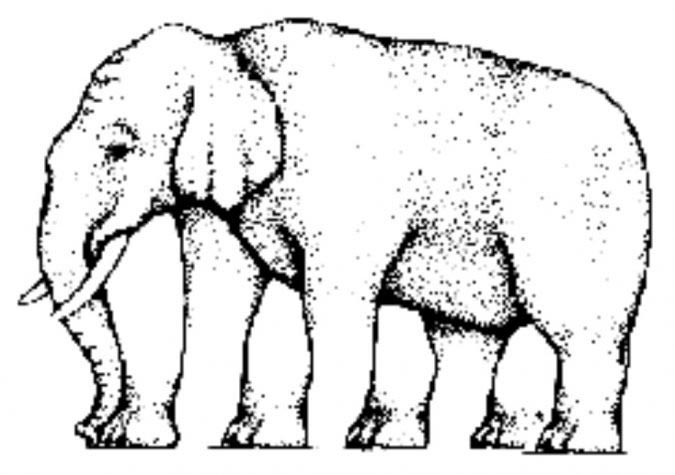
Сколько ног у слона?
Несмотря на оптическую иллюзию, на самом деле у этого слона только одна правильная нога!
Видео:Найдите третью сторону треугольникаСкачать

Загадка
Мужчина стоит на одной стороне реки, его собака — на другой. Как только мужчина зовет собаку, то она тут же бежит к нему, пересекая реку, не промокнув и не используя ни мост, ни лодку. Как собака это сделала?
Ответ: река замёрзла.
Видео:Теорема о трёх медианахСкачать

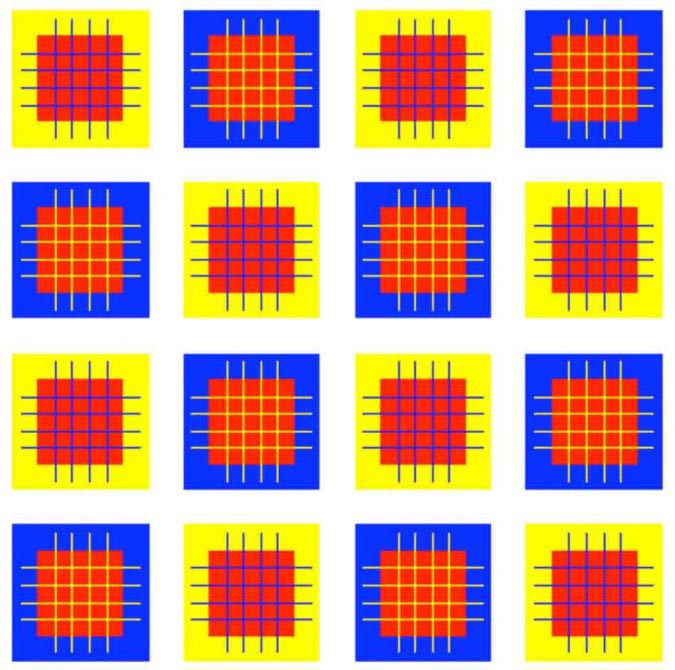
Квадраты внутри синих и желтых квадратов одного цвета?
Ответ: Да, они одного цвета!
Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

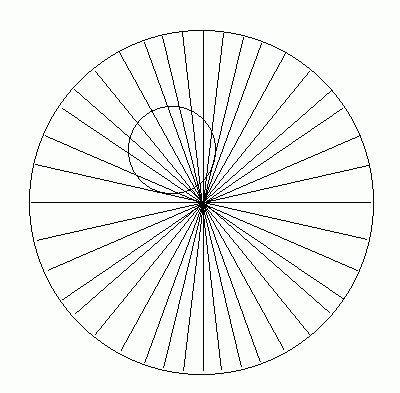
Ровный ли круг внутри большого круга?
Ответ: да, они оба ровные!
Видео:Геометрия 8 класс. Урок 1. Четырехугольник и его элементыСкачать

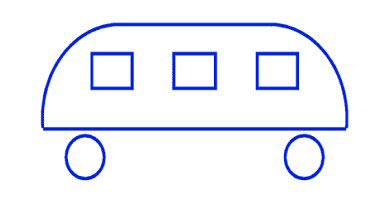
В какую сторону едет автобус?
Самое забавное, что если спросить ребенка, то скорее всего он сразу даст правильный ответ.
Ответ: влево, потому что на рисунке не видно дверей.
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

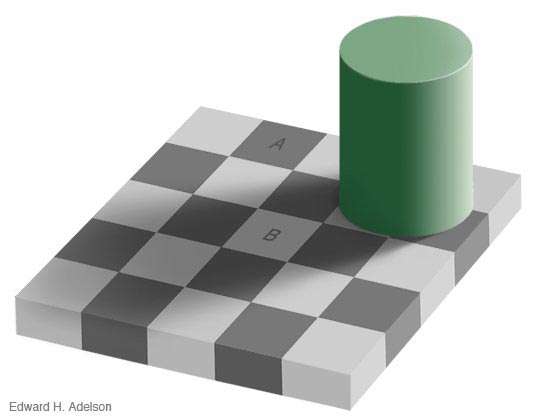
Какой из этих квадратов темнее: А или В?
Ответ: на самом деле они одного и того же цвета!
Видео:Задача на логику как разрезать на две части и получить квадрат?Скачать

Загадка: положи меня на одну из моих сторон, и я всё. Сложи меня пополам, и я ничто. Что я?
Ответ: цифра 8.
Почему? Если «положить» 8 на одну из сторон, то цифра превратиться в знак бесконечности, а если сложить её пополам, то получится ноль.
Видео:✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Это перевёрнутое лицо Линкольна вам кажется нормальным?
Оно кажется таковым, пока вы не попробуете перевернуть картинку.
На самом деле на этом фото перевёрнуто всё, кроме глаз.
Видите черные круги на пересечении белых линий?
Но на самом деле на картинке нет никаких чёрных кругов, и это снова всего лишь наши глаза.
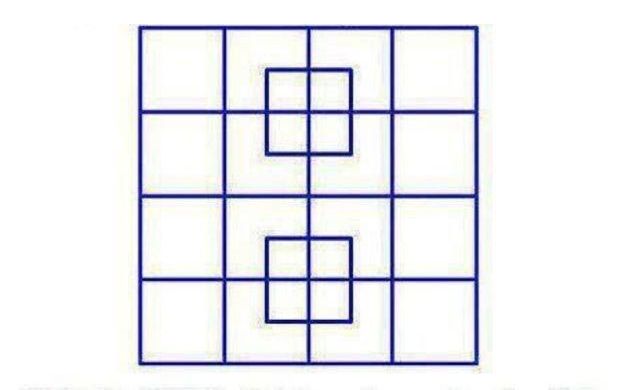
Сколько квадратов на этой картинке?
Попробуйте найти все квадраты.
Ответ: на самом деле их 40!
Горизонтальные линии разной длины?
Ответ: на самом деле они одинаковые, хотя нижняя кажется заметно длиннее.
Последняя загадка
Если я у вас есть, то вы хотите мной поделиться. Если вы мной поделитесь, то меня у вас больше не будет. Что я?
Ответ: секрет!
Поделитесь с друзьями головоломными загадками и подразните их мозг!
Не забудьте также узнать гениальный способ, которым при помощи трёх собак и теннисного мячика можно восстановить сгоревший лес.
Головоломка Волшебный треугольник
Головоломка «Волшебный треугольник» будет интересна и доступна для решения детям школьного возраста.
Есть несколько разных видов волшебных треугольников, и я поделюсь с вами двумя из них. Самое замечательное то, что у каждой головоломки есть несколько решений.
Решение волшебных треугольников развивает у детей базовые навыки сложения, а также критическое и логическое мышление.
Вам понадобится
- Ребенок! (подойдет один или несколько).
- Распечатанный шаблон.
Или свой собственный карандашом и бумагой.
Можно решить волшебный треугольник, написав цифры внутри кругов. Но проще исправлять ошибки, имея возможность перемещать круги вдоль периметра треугольника.
Цель игры
Расположите числа для каждого треугольника (1-6 для треугольника 3x3x3; 1-9 для треугольника 4x4x4) так, чтобы сумма чисел на каждой стороне была равна сумме чисел на каждой другой стороне.
Для маленького треугольника расположите числа так, чтобы сумма каждой стороны равнялась 9. Есть также решения для 10, 11 и 12.
Для большого треугольника расположите числа так, чтобы сумма каждой стороны равнялась 17. Вы также можете найти решения для чисел 19, 20, 21 и 23.
Если ребенок силен в математике, не говорите ему, какой будет сумма для каждой стороны волшебного треугольника. Просто дайте указание расположить числа так, чтобы сумма на каждой стороне была равна остальным. Пусть он попробует вычислить, например, что каждая сторона должна давать в сумме 9.
Эту загадку можно собрать с треугольниками еще большего размера — по 5 или 6 цифр на каждой стороне. Однако вам придется сделать свою собственную игровую доску!
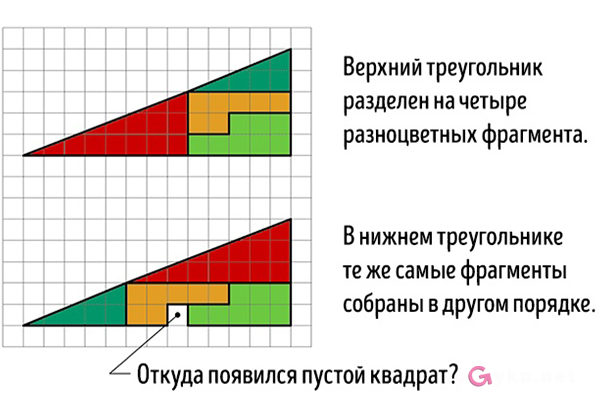
Задачка на сообразительность: откуда появился лишний пустой квадрат?
Откуда появился лишний пустой квадрат?
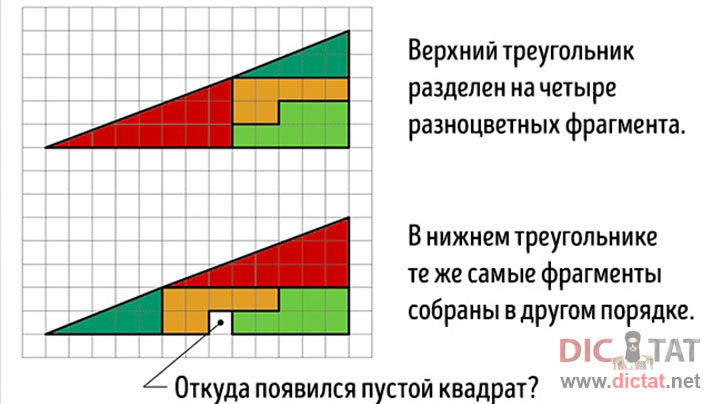
Перед вами два треугольника. Верхний разделен без остатка на четыре фрагмента, окрашенные разными цветами. В нижнем треугольнике те же самые фрагменты расположены в другом порядке. Внимание, вопрос. Откуда взялся лишний пустой квадрат? Ответ внутри.
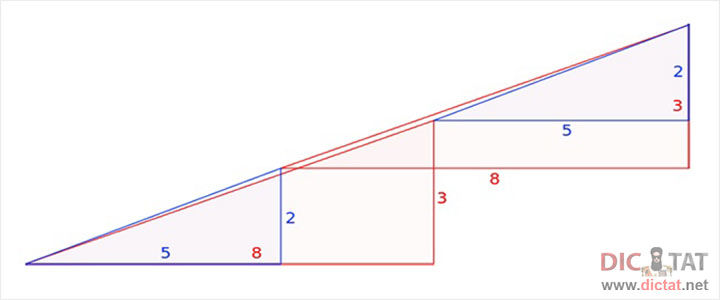
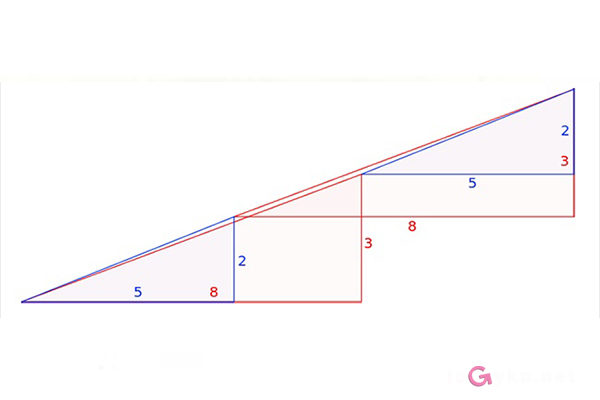
В действительности это не оптический обман, а интересная задача. Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади (S13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это — вогнутый 4-угольник). Это отчётливо заметно на рисунке-схеме ниже — «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) — внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.
Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу (2/3 и 5/8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Назовём первую фигуру, являющуюся вогнутым четырёхугольником, и вторую фигуру, являющуюся вогнутым восьмиугольником, псевдотреугольниками. Если нижние стороны этих псевдотреугольников параллельны, то гипотенузы в обоих псевдотреугольниках 13×5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем — наружу). Если наложить верхнюю и нижнюю фигуры 13×5 друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «лишняя» площадь. На рисунке-схеме этот параллелограмм приведён в верных пропорциях.
Острый угол в этом параллелограмме равен arcctg 46 ≈ 0°1′18,2″. На такой угол минутная стрелка на исправных часах сдвигается за 12,45 с. Именно на такую величину тупой угол в рассматриваемом параллелограмме отличается от развёрнутого. Визуально столь ничтожное отличие незаметно, зато оно хорошо просматривается на анимации.
По словам Мартина Гарднера, эту задачу изобрёл иллюзионист-любитель из Нью-Йорка Пол Карри в 1953. Однако принцип, заложенный в неё, был известен ещё в 1860-е годы. Можно заметить, что длины сторон фигур из данной задачи (2, 3, 5, 8, 13) являются последовательными числами Фибоначчи.
ЗАДАЧА, КОТОРУЮ МОЖЕТ РЕШИТЬ ТОЛЬКО 22% ЛЮДЕЙ
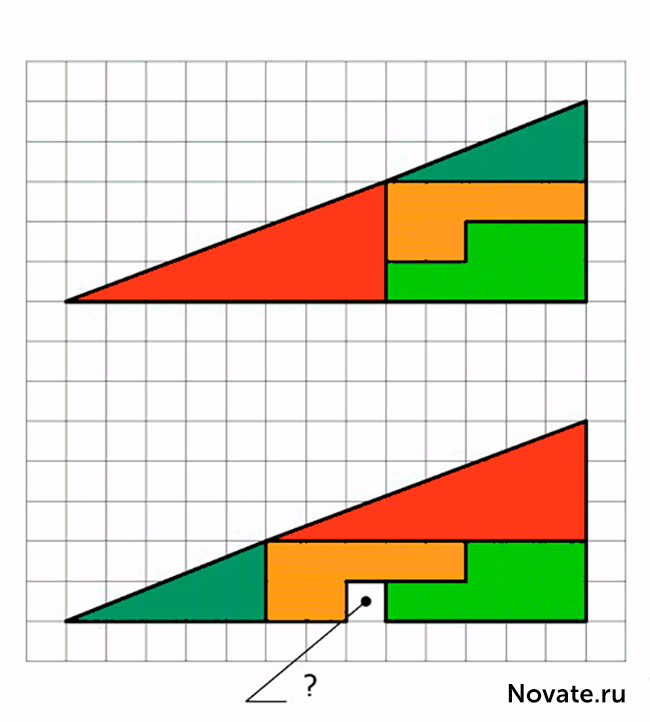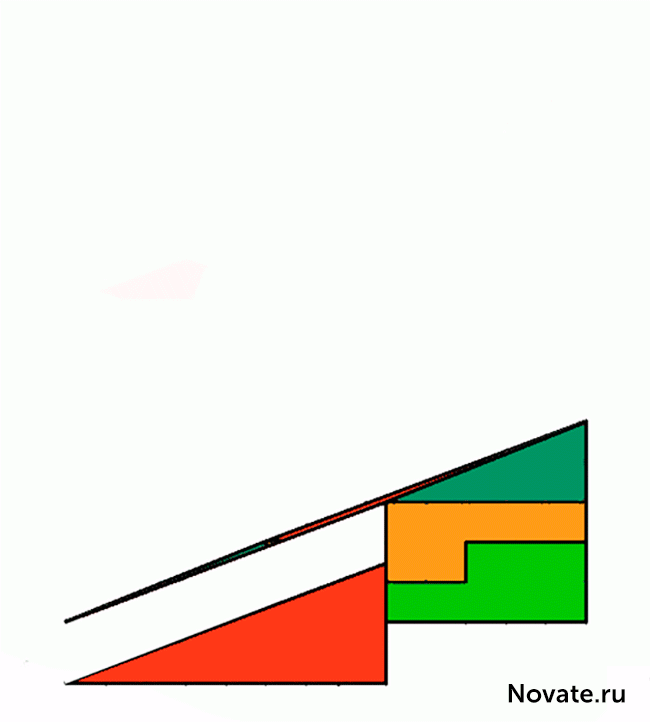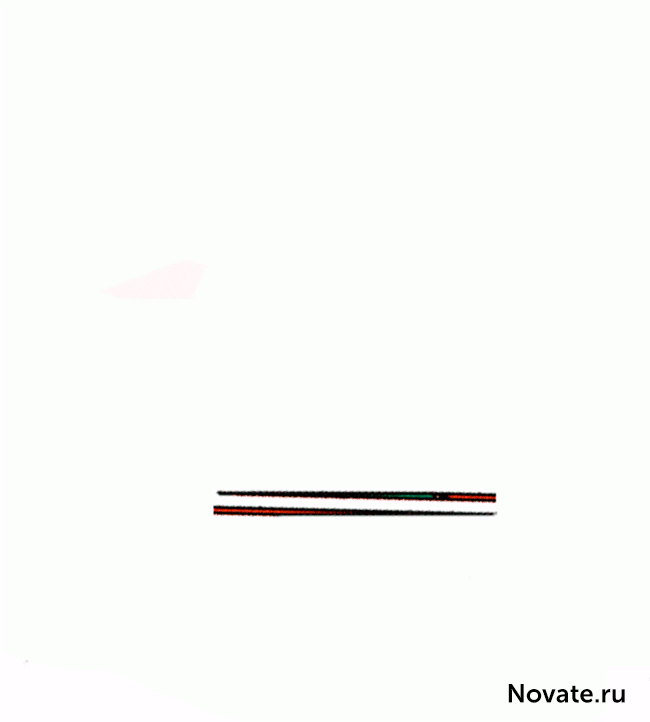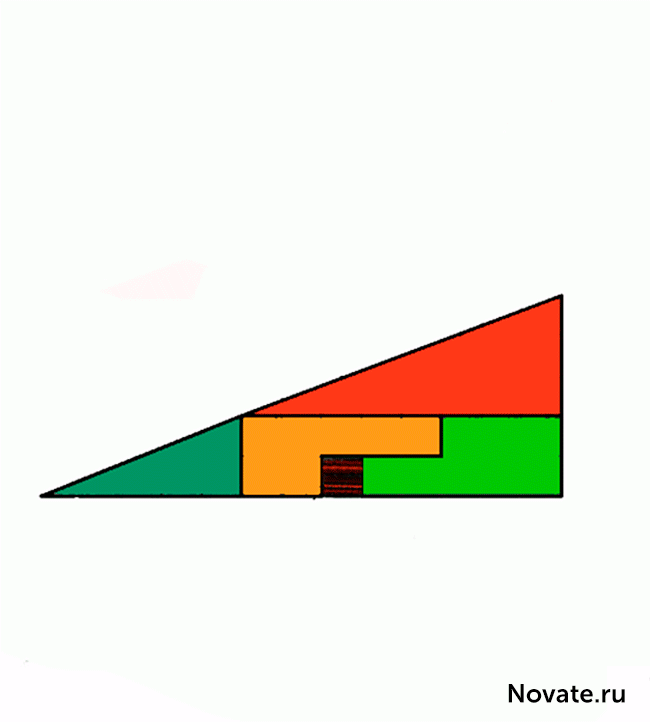
Перед вами два треугольника. Верхний разделен без остатка на 4 фрагмента, окрашенных разными цветами. В нижнем треугольнике те же самые фрагменты расположены в другом порядке. Внимание, вопрос: откуда взялся лишний пустой квадрат?
В действительности это не оптический обман, а интересная задача. Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако то, что визуально наблюдается как треугольники 13 × 5, на самом деле таковым не является и имеет разные площади (S 13 × 5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура названа треугольником (на самом деле это вогнутый четырехугольник). Это отчетливо заметно на рисунке-схеме ниже, где «гипотенузы» верхней и нижней фигур проходят через разные точки: вверху (8,3) и внизу (5,2). Секрет — в свойствах синего и красного треугольников. Это легко проверить вычислениями.
Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу (2/3 и 5/8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Назовем первую фигуру, являющуюся вогнутым четырехугольником, и вторую фигуру, являющуюся вогнутым восьмиугольником, псевдотреугольниками. Если нижние стороны этих псевдотреугольников параллельны, то гипотенузы в обоих псевдотреугольниках 13 × 5 на самом деле являются ломаными линиями (на верхнем рисунке создается излом внутрь, а на нижнем — наружу). Если наложить верхнюю и нижнюю фигуры 13 × 5 друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «лишняя» площадь. На рисунке-схеме этот параллелограмм приведен в верных пропорциях.
Острый угол в этом параллелограмме равен arcctg 46 ≈ 0°1′18,2″. На такой угол минутная стрелка на исправных часах сдвигается за 12,45 сек. Именно на такую величину тупой угол в рассматриваемом параллелограмме отличается от развернутого. Визуально столь ничтожное отличие незаметно, зато оно хорошо просматривается на анимации.
Перед вами два треугольника
Давайте отвлечемся от всех дел и попробуем решить задачку на логику. Решение очень простое, нужно только внимательно посмотреть на рисунок.
Перед вами два треугольника. Верхний разделен без остатка на 4 фрагмента, окрашенных разными цветами. В нижнем треугольнике те же самые фрагменты расположены в другом порядке. Внимание, вопрос: откуда взялся лишний пустой квадрат?
Ответ:
В действительности это не оптический обман, а интересная задача. Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако то, что визуально наблюдается как треугольники 13 × 5, на самом деле таковым не является и имеет разные площади (S 13 × 5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура названа треугольником (на самом деле это вогнутый четырехугольник). Это отчетливо заметно на рисунке-схеме ниже, где «гипотенузы» верхней и нижней фигур проходят через разные точки: вверху (8,3) и внизу (5,2). Секрет — в свойствах синего и красного треугольников. Это легко проверить вычислениями.
По словам Мартина Гарднера, эту задачу изобрел иллюзионист-любитель из Нью-Йорка Пол Карри в 1953 году. Однако принцип, заложенный в нее, был известен еще в 1860-е годы. Можно заметить, что длины сторон фигур из данной задачи (2, 3, 5, 8, 13) являются последовательными числами Фибоначчи