Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса
Применим теорему синусов к треугольнику ABC:
Приведём другое решение.
Вписанный угол дополняет половину центрального угла, опирающегося на ту же хорду, до 180°, значит, По теореме косинусов:
Ошибка в последней строчке. Перед 6 не плюс, а минус.
В последней строчке все верно: .
Хорда AB делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Из точки C хорда АВ видна под углом АCВ. Пусть большая часть окружности равна 7x, тогда меньшая равна 5x.
Значит, меньшая дуга окружности равна 150°, а большая — 210°. Вписанный угол равен половине дуги, на которую он опирается, значит, опирающийся на большую дугу угол АCВ равен 105°.
В условии сказано под меньшей дугой окружности, a в ответе дано под большей. Правильно?
Решение верно, по условию точка лежит на меньшей дуге.
Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Угол между касательной и хордой равен половине дуги, заключённой между ними. Поэтому он равен 46.
Через концы А и В дуги окружности с центром О проведены касательные АС и ВС. Угол СAB равен 32°. Найдите угол AОB. Ответ дайте в градусах.
Угол между касательной и хордой, проведённой в точку касания, измеряется половиной дуги, заключённой между его сторонами. Поэтому величина меньшей дуги АВ окружности равна 64°. Центральный угол измеряется дугой, на которую он опирается, поэтому угол АОВ равен 64°.
Примечание об изменении задания.
Ранее это задание и аналогичные к нему в Открытом банке были формулированы иначе.
Задание.Угол между хордой AB и касательной BC к окружности равен 32°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
Решение. Угол между касательной и хордой, проведённой в точку касания, измеряется половиной дуги, заключённой между его сторонами. Значит, искомая величина дуги равна 64°.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Угол между касательной и хордой
Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Касательная перпендикулярна радиусу, проведенному в точку касания.
Пусть . Тогда . Треугольник ОСА – равнобедренный, ОА = ОС (как радиусы окружности). Значит, , что и требовалось доказать.
Заметим, что – как вписанный, опирающийся на ту же дугу.
Задача ЕГЭ по теме «Угол между касательной и хордой»
Угол между хордой AB и касательной BC к окружности равен . Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
Касательная ВС перпендикулярна радиусу ОВ, проведенному в точку касания. Значит, угол ОВС равен 90°, и тогда угол ОВА равен . Угол ОАВ также равен 58°, так как треугольник ОАВ – равнобедренный, его стороны ОА и ОВ равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол АОВ, равен .
Центральный угол равен угловой величине дуги, на которую он опирается, и тогда дуга АВ равна .
Эту задачу можно решить быстрее, зная теорему об угле между касательной и хордой.
Угол между касательной и хордой, проведенной через точку касания, — это угол АВС. Он равен половине угловой величины дуги, заключенной между касательной ВС и хордой АВ, то есть дуги АВ. Значит, дуга АВ равна .
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Углы, связанные с окружностью
 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:Угол между хордой и касательной. 9 класс.Скачать
Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Угол между хордой и касательнойСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Угол между хордой и касательнойСкачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство 🔥 ВидеоСекретная теорема из учебника геометрииСкачать  Угол между касательной и хордойСкачать 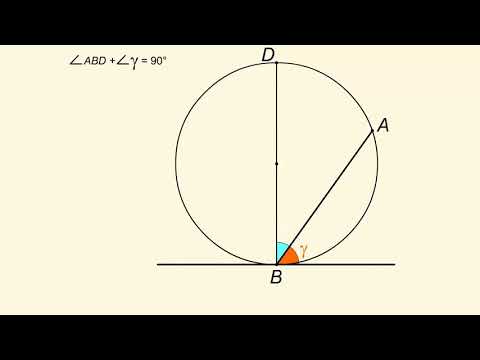 Найти угол между касательной и хордой. Полная версияСкачать  Геометрия 11 класс. Угол между касательной и хордойСкачать  Задача 6 №27877 ЕГЭ по математике. Урок 118Скачать  Хорда АВ стягивает дугу окружности в 40 градусов. Найдите угол АВС между этой хордой и касательной..Скачать  Задача 6 №27878 ЕГЭ по математике. Урок 119Скачать  Угол между касательной и хордойСкачать  Геометрия Угол между касательной к окружности и хордой, проведенной через точку касания, измеряетсяСкачать  #59. Олимпиадная задача о касательной к окружности!Скачать  Окружность..Угол между касательной и хордой.Скачать  Угол между касательной и хордой | Задачи 1-10 | Решение задач | Волчкевич|Уроки геометрии 7-8 классыСкачать  Окружность.Отношение между хордой и касательной.Скачать  Угол между касательной и хордой.Скачать  |




































