Параллельные прямые с и в пересечены двумя параллельными секущими ав

Итоговая контрольная работа по геометрии в 7 классе с ответами УМК Атанасян Просвещение (средний уровень). Урок 68 поурочного планирования по геометрии. Геометрия 7 Атанасян К-6 Уровень 2 (варианты 3, 4). Цитаты использованы в учебных целях.

Другие варианты итоговой контрольной работы в 7 классе:

Итоговая контрольная работа по геометрии
Уровень 2 (средний). Геометрия 7 класс

Вариант 3

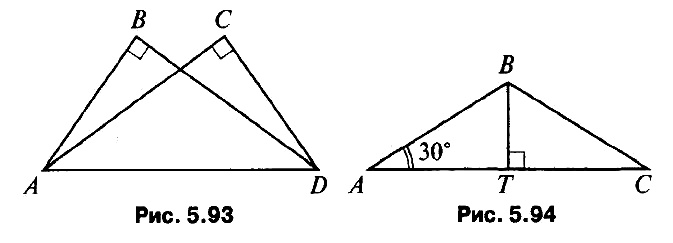
1. Дано: ∠B = ∠C = 90°, ∠ADC = 50°, ∠ADB = 40° (рис. 5.93). Доказать: ΔABD = ΔDCA.
2. В равнобедренном треугольнике угол между боковыми сторонами в три раза больше угла при основании. Найдите углы треугольника.
3. Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С лежат на прямой а, а точки В и D — на прямой b. Доказать: АС = BD.
4. * Дано: АВ = ВС, ВТ = 4 см (рис. 5.94).
   а) Между какими целыми числами заключена длина отрезка АС?
   б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.

Вариант 4

1. Дано: ∠B = ∠C = 90°, ∠ADB = 40°, ∠BDC = 10° (рис. 5.95). Доказать: ΔABD = ΔDCA.
2. В равнобедренном треугольнике угол при основании в четыре раза больше угла между боковыми сторонами. Найдите углы треугольника.
3. Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки В и D — прямой b. Доказать: АВ = CD.
4. * Дано: АВ = ВС, АС = 10 см (рис. 5.96).
   а) Между какими целыми числами заключена длина высоты AВС?
   б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.

Решения и ответы на контрольную работу:

ОТВЕТЫ на Вариант 3

№ 1. Сумма острых углов прямоугольного треугольника равна 90°.
ΔADC: ∠ACD = 90°, ∠ADC = 50°, ⇒ ∠ ACD = 90° — 50° = 40°
В прямоугольных треугольниках ABD и DCA общая гипотенуза AD и одинаковые острые углы (∠ACD = ∠ADB = 40°), ⇒ ΔABD = ΔDCA по гипотенузе и острому углу.

№ 2. В равнобедренном треугольнике углы при основании равны. А сумма углов треугольника равна 180°. Будем решать алгебраическим способом. Для удобства, назовем треугольник ABC, а бОльшим будем угол A.
Пусть угол В = х. Тогда угол С= х, а угол А равен 3х (в три раза больше). Их сумма равна х+х+3х. А по теореме суммы углов треугольника 180°. Составим уравнение: х + х + 3х = 180. Решив уравнение получим: х = 36.
Значит, угол В (при основании) равен 36°, угол С (тоже при основании) равен 36°, а угол А = 36 • 3 = 108°
Ответ: углы треугольника равны 36°, 36° и 108°.

№ 3. По условию параллельные прямые а и b пересекаются двумя параллельными секущими АВ и СD, в результате этого получается четырехугольник АВСD, в котором пары противолежащих сторон АВ и СD, АС и ВD (принадлежащие прямым а и b) параллельны, значит полученный четырехугольник АВСD является параллелограммом. Противолежащие стороны параллелограмма равны, значит АС = BD, что и требовалось доказать.

№ 4. а) между числами 13 и 14.

ОТВЕТЫ на Вариант 4

№ 1. а) ∠ADC = ∠ADB + ∠BDC = 40° + 10 °= 50°. б) ∠BAD = 180 — ∠ABD — ∠ADB = 180° — 90° — 40° = 50°. в) ∠BAD = ∠ADC = 50°; ∠ABD = ∠ACD = 90°; гипотенуза AD общая. Отсюда следует, что треугольники равны (если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны).

№ 2. Пусть ∠A и ∠С – углы при основании, а ∠В – угол между боковыми сторонами. Так как треугольник равнобедренный, то ∠A = ∠C. Угол В обозначим х, тогда ∠A = ∠C = 4х. Составим уравнение: x + 4x + 4x = 180°. Отсюда следует, что x = 20° = ∠B. Тогда ∠A = 4 • 20 = 80° = ∠C. Ответ: углы треугольника равны 80°, 80° и 20°.

№ 3. Проведем диагональ AD и докажем, что △ABD = △ACD. Так как a параллельно b, значит накрест лежащие углы равны: ∠BAD = ∠ADC и ∠BDA = ∠CAD. AD — общая, значит △ABD = △ACD по стороне и прилежащим углам. Следовательно, AB = CD

№ 4. a) Между числами 8 и 9.

Информация для учителя:

По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.

Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

Другие варианты итоговой контрольной работы в 7 классе:

Вы смотрели: Итоговая контрольная работа по геометрии в 7 классе с ответами УМК Атанасян Просвещение (средний уровень). Урок 68 поурочного планирования по геометрии. Геометрия 7 Атанасян К-6 Уровень 2 (варианты 3, 4).

В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Параллельные прямые a и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки B и D — прямой b?

Геометрия | 5 — 9 классы

Параллельные прямые a и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки B и D — прямой b.

Докажите что АВ = CD P.

S. если можно с чертежом пожалуйста : ).

Две пары пересекающихся параллельных прямых отсекают четырехугольник ABCD, противоположные стороны которого попарно параллельны.

Принадлежат параллельным прямым.

В параллелограмме противоположные стороны равны.

АВ и СD — противоположные стороны параллелограмма.

В получившемся четырехугольнике соединим А и D.

Треугольники АСD иимеют равные накрестлежащиеуглы при пересечении параллельных прямых а иb секущей AD, и той же секущей при пересечении параллельных прямых AB и CD, а сторона AD — общая.

Второй признак равенства треугольников.

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

Видео:29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

1. в равнобедренном треугольнике угол при основании в 4 раза больше угла между боковыми сторонами?

1. в равнобедренном треугольнике угол при основании в 4 раза больше угла между боковыми сторонами.

Найдите углы треугольника

Параллельные прямые a и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки B и D — прямой b.

Докажите что АВ = CD.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Паралельные прямые а и в пересечены дввумя параллельными секущими АВ и СD, причем А и С принадлежат прямой а, В и D прямой в докажитк что АС = ВD?

Паралельные прямые а и в пересечены дввумя параллельными секущими АВ и СD, причем А и С принадлежат прямой а, В и D прямой в докажитк что АС = ВD.

Видео:Свойства углов, образованных двумя параллельными прямыми и секущей Задачи на признаки параллельностСкачать

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причём точки A и C принадлежат прямой a, а точки B и D — прямой b?

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причём точки A и C принадлежат прямой a, а точки B и D — прямой b.

Докажите, что AB = CD.

Видео:Углы, образованные при пересечении двух прямых секущейСкачать

Через точку А проведите прямую, параллельную прямой CD Помогите пожалуйста?

Через точку А проведите прямую, параллельную прямой CD Помогите пожалуйста.

Видео:№211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисыСкачать

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причем точки A и C лежат на прямой a, а точки B и D — на прямой b?

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причем точки A и C лежат на прямой a, а точки B и D — на прямой b.

Докажите, что AC = BD.

Видео:Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

Две параллельные прямые пересечены секущей?

Две параллельные прямые пересечены секущей.

Докажите, что : биссектрисы накрест лежащих углов параллельны.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

1. Прямые, которые не пересекаются, называются……?

1. Прямые, которые не пересекаются, называются…….

2. Утверждение, принимаемое без доказательства, называется….

3. Если при пересечении двух прямых секущей….

, то прямые параллельны.

4. Если две параллельные прямые пересечены секущей, то сумма ….

5. Через точку, не лежащую на данной прямой, можно провести….

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причем точки A и C лежат на прямой a, а точки В и D – на прямой b?

Параллельные прямые a и b пересечены двумя параллельными секущими AB и CD, причем точки A и C лежат на прямой a, а точки В и D – на прямой b.

Докажите, что АС = ВD.

Видео:Углы, образованные параллельными прямыми и секущейСкачать

Прямые АВ и CD пересечены секущей MN в точках К м Р соответственно?

Прямые АВ и CD пересечены секущей MN в точках К м Р соответственно.

Являются ли прямые АВ и CD параллельными, если угол ВКР = 112° и угол КРD = 58°?

Видео:№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Если две параллельные прямые пересечены секущей, то?

Если две параллельные прямые пересечены секущей, то.

На странице вопроса Параллельные прямые a и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки B и D — прямой b? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Видео:Параллельные прямые (задачи).Скачать

Параллельность прямых

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Теоремы об углах, образованных двумя параллельными прямыми и секущей.Скачать

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

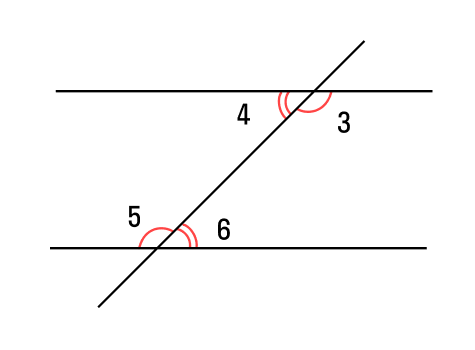
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

два внутренних односторонних угла образуют в сумме 180°:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

два внутренних накрест лежащих угла равны между собой:

два соответственных угла равны между собой:

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

🔍 Видео

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210Скачать

Геометрия 7 класс. Теоремы об углах, образованных двумя параллельными прямымСкачать

№557. Стороны угла А пересечены параллельными прямыми ВС и DE, причем точки В и D лежатСкачать

Теоремы об углах, образованных двумя параллельными прямыми и секущей. Решение задач.Скачать