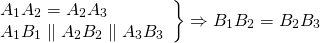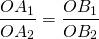Параллельные прямые отсекают на сторонах угла отрезки соответственно равные 5 и 6 на одной стороне

Впишите правильный ответ.

Впишите правильный ответ.

Впишите правильный ответ.

Впишите правильный ответ.

Впишите правильный ответ.

В треугольнике ABCAM = MB = 8 см, AC = 21 см, BK = 9 см.
Найдите периметр ABC, если MK

AC. Ответ дайте в сантиметрах.
Ответ: см.

Выберите правильный ответ.

Две параллельные прямые отсекли на одной стороне угла, считая от вершины, отрезки
6 см и 8 см, на другой стороне угла больший отрезок равен 12 см. Найдите меньший
из отрезков, полученных на второй стороне угла. Ответ дайте в сантиметрах.

Видео:Теорема Фалеса. 8 класс.Скачать

Теорема Фалеса

Теорема Фалеса может быть сформулирована не только для угла, но и для прямых. Кроме того, существует еще и обобщенная теорема Фалеса.

Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Теорема Фалеса может быть сформулирована не только для угла, но и для прямых.

Если параллельные прямые пересекают две данные прямые и отсекают на одной прямой равные отрезки, то они отсекают равные отрезки и на другой прямой.

Теорема о пропорциональных отрезках (обобщенная теорема Фалеса).

Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Теорема Фалеса и ее модификации применяется в том числе, и в задачах на построение (в частности, для деления отрезка на n равных частей и при построении четвертого пропорционального отрезка).

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Презентация по геометрии «Теорема Фалеса»

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Деление отрезка на равные части. Теорема Фалеса. ЧерчениеСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Теорема Фалеса Теорема. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне (рис. а). Теорему Фалеса можно применять для деления отрезка на n равных частей (рис. б).

Отношением двух отрезков AB и CD называется число, показывающее сколько раз отрезок CD и его части укладываются в отрезке АВ. Теорема о пропорциональных отрезках Говорят, что отрезки АВ, CD пропорциональны отрезкам A1B1, C1D1, если равны их отношения

Теорема. (обобщенная теорема Фалеса) Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Пример 1 Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A, B и C, D соответственно. Найдите OA, если OB = 15 см и OC : OD = 2 : 5. Ответ: 6 см.

Пример 2 Докажите, что биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам. Решение: Пусть CD биссектриса треугольника ABC. Докажем, что AD : DB = AC : BC. Проведем прямую BE, параллельную CD. В треугольнике BEC угол B равен углу E. Следовательно, BC = EC. По следствию из теоремы о пропорциональных отрезках, AD : DB = AC : CE = AC : BC.

Упражнение 1 Определите, пропорциональны ли пары отрезков а, b и c, d, если: а) a = 0,8 см, b = 0,3 см, с = 2,4 см, d = 0,9 см; б) а = 50 мм, b = 6 см, с = 10 см, d = 18,5 см. Ответ: а) Да; б) нет.

Упражнение 2 Среди отрезков a, b, c, d, e выберите пары пропорциональных отрезков, если а = 2 см, b = 17,5 см, с = 16 см, d = 35 см, е = 4 см. Ответ: a, e и b, d.

Упражнение 3 Даны три отрезка: а, b, и с. Какова должна быть длина четвертого отрезка d, чтобы из них можно было образовать две пары пропорциональных отрезков, если а = 6 см, b = 3 cм, с = 4 см, и отрезок d больше каждого из этих отрезков. Ответ: 8 см.

Упражнение 6 На одной из сторон угла расположены два отрезка 3 см и 4 см. Через их концы проведены параллельные прямые, образующие на другой стороне также два отрезка. Больший из отрезков равен 6 см. Чему равен другой отрезок? Ответ: 4,5 см.

Упражнение 7 Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A, B и C, D соответственно. Найдите: а) CD, если OA = 8 см, AB = 4 см, OD = 6 см; б) OC и OD, если OA : OB = 3 : 5 и OD – OC = 8 см; в) OA и OB, если OC : CD = 2 : 3 и OA + OB = 14 см. Ответ: а) 2 см; б) 12 см и 20 см; в) 4 см и 10 см.

Упражнение 8 Проекции двух сторон остроугольного треугольника АВС на прямую АС имеют длины 6 см и 4 см. Какую длину имеют проекции медиан этого треугольника на ту же прямую? Ответ: 1 см, 7 см и 8 см. А В С М D К

Упражнение 9 Каждая из сторон треугольника разделена на три равных отрезка и точки деления соединены отрезками. Найдите периметр образовавшейся при этом фигуры, если периметр исходного треугольника равен p. Ответ: p.

Упражнение 11 Ответ: cм.

Упражнение 12 В треугольнике АВС сторона ВС разделена на четыре равные части и через полученные точки деления проведены прямые, параллельные стороне АВ, равной 18 см. Найдите отрезки этих прямых, заключенные внутри треугольника. Ответ: 4,5 см, 9 см, 13,5 см.

Упражнение 13 Основания трапеции равны 14 см и 20 см. Одна из боковых сторон разделена на три равные части и через точки деления проведены прямые, параллельные основаниям трапеции. Найдите отрезки этих прямых, заключенные внутри трапеции. Ответ: 16 см и 18 см.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 338 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

• Стукалова Екатерина БорисовнаНаписать 1308 06.02.2018

Номер материала: ДБ-1128671

05.02.2018 480

04.02.2018 596

04.02.2018 762

04.02.2018 253

04.02.2018 372

04.02.2018 1023

04.02.2018 160

04.02.2018 180

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔥 Видео

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать

Теорема о пропорциональных отрезкахСкачать

Параллельные прямые (задачи).Скачать

Пропорциональные отрезки. Медианы в треугольнике. Теорема Фалеса. Задачи для ОГЭ и ЕГЭ.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Геометрия 8 класс : Теорема ФалесаСкачать

Теорема Фалеса. Практическая часть - решение задачи. 8 класс.Скачать

Теорема Фалеса. Практическая часть - решение задачи. 8 класс.Скачать

Геометрия 7 класса в одной задаче. Геометрия 7 класс кратко | МатематикаСкачать

Задачи на параллельность и сумму углов, 7 класс, Математическая вертикальСкачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Геометрия. 8 класс. Урок 6 "Теорема Фалеса. Теорема о пропорциональных отрезках"Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Геометрия. 8 класс. Теорема Фалеса. Пропорциональные отрезки /06.10.2020/Скачать

Теорема о пропорциональных отрезках. Теорема ФалесаСкачать