Параллельные прямые делят отрезки на равные части (3 видео)

4.5. Теорема Фалеса. Разбиение отрезка на заданное число равных частей

Теорема Фалеса

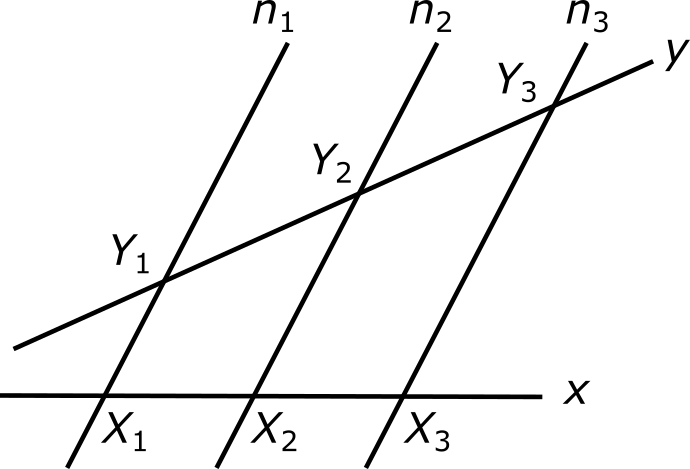
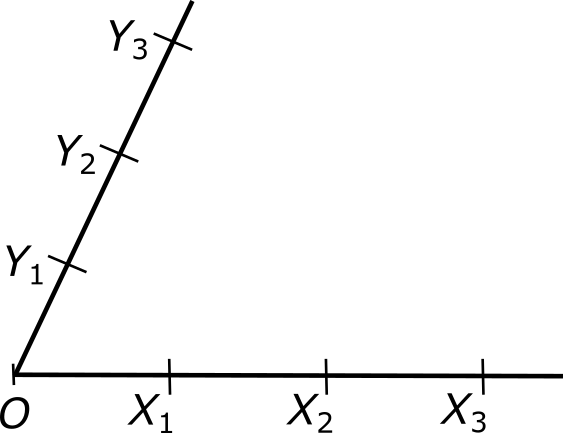
Пусть, далее, про точки X₁, X₂ и X₃, расположенные на прямой x, известно, что они следуют друг за другом через равные расстояния, так что |X₁X₂| = |X₂X₃|. Мы собираемся теперь доказать, что точки Y₁, Y₂ и Y₃, расположенные на прямой y, также следуют друг за другом через равные расстояния: |Y₁Y₂| = |Y₂Y₃|. Это утверждение известно как теорема Фалеса. (Под теоремами математики понимают важные утверждения, которые можно доказать на основании ранее установленных фактов. Некоторые из теорем называются именами выдающихся математиков — как в данном случае.)

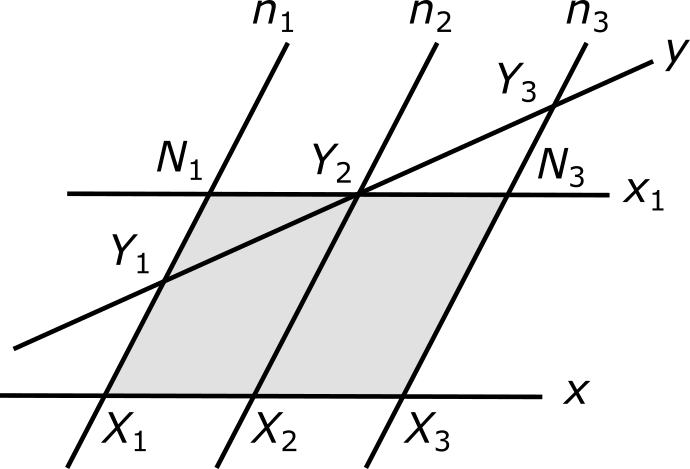
Приступаем к доказательству. Для этого через точку Y₂ проведем прямую x₁, параллельную прямой x. У нас образовалось два параллелограмма с общей стороной X₂Y₂.

Обозначим точки пересечения прямой x₁ с прямыми n₁ и n₃ как N₁ и N₃, соответственно. Теперь мы можем обозначить параллелограммы по их вершинам как X₁X₂Y₂N₁ и X₂X₃N₃Y₂. Поскольку у параллелограммов противоположные стороны равны между собой, то

Таким образом, точка Y₂ является серединой отрезка N₁N₃, а значит,

параллельные прямые n₁ и n₃ симметричны относительно точки Y₂.

Прямая y также симметрична относительно точки Y₂, поскольку она проходит через эту точку.

Разбиение отрезка на заданное число равных частей

Допустим нам требуется разбить некоторый отрезок OX на три равные части. Теорема Фалеса дает нам возможность сделать это легко и изящно.

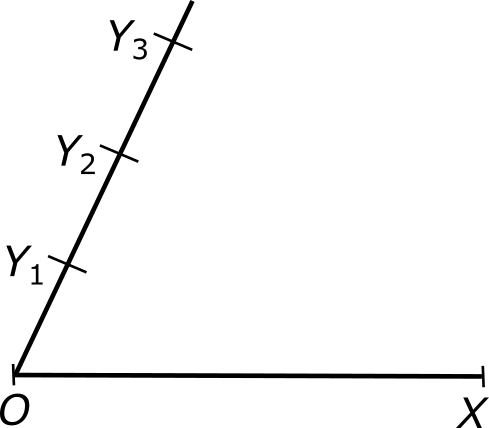
Проведем от точки O произвольный луч, который образует с отрезком OX любой угол, кроме нуля и 180° (на практике, однако, удобно брать угол в пределах приблизительно от 30° до 90°).

Отметим на этом луче три точки Y₁ Y₂ и Y₃ с одинаковым шагом, начиная от точки O, так чтобы выполнялось соотношение
|OY₁| = |Y₁Y₂| = |Y₂Y₃|.
(Длина шага принципиальной роли не играет и выбирается из соображения удобства. Например, мы можем приставить к лучу линейку и сделать на нем три засечки через каждый сантиметр. Другая возможность заключается в том, чтобы делать шаги циркулем с фиксированным расстоянием между концами.)

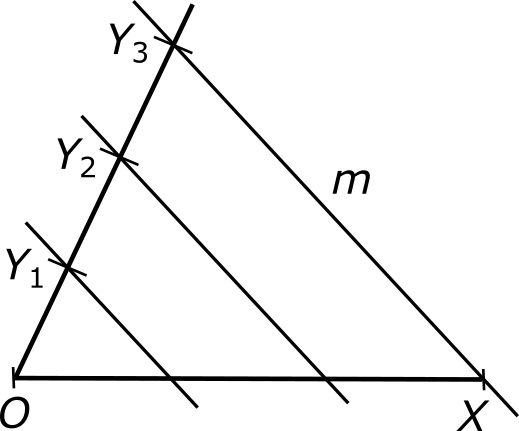
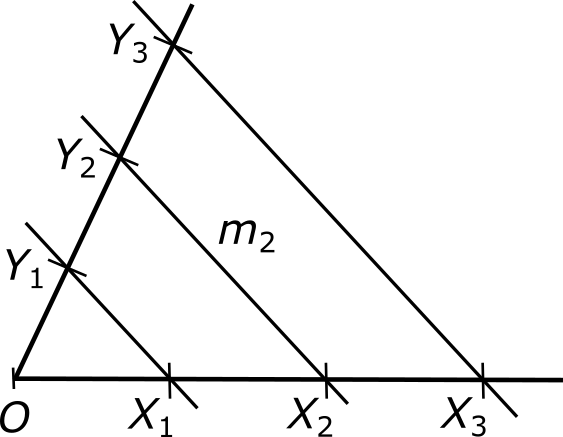
Через точку Y₃ и второй конец исходного отрезка — точку X — проведем прямую m.

Через остальные точки, отмеченные на луче, проведем прямые, параллельные прямой m. Согласно теореме Фалеса, эти прямые, пересекая отрезок OX, разобьют его на три равные части.

Подобным же образом, произвольный отрезок можно разбить на любое другое число равных частей.

Еще один способ построения параллельных прямых

Пусть дан угол X₁OY₁ (не равный нулю и не равный 180°) с вершиной в точке O и со сторонами, проходящими через некоторые точки X₁ и Y₁.

Очевидно, что в этом геометрическом построении ряды точек можно продолжить, соблюдая выбранный шаг, так что:

Рассуждая, как раньше, можно доказать, что все прямые, проходящие через точки X и Y с одинаковыми индексами, параллельны между собой.

Конспект

Теорема Фалеса: Если три параллельные прямые отсекают на некоторой четвертой прямой два равных по длине отрезка, то при пересечении с какой-либо пятой прямой они также отсекут два отрезка равной длины.

Разбиение отрезка OX на n равных частей:

Строим произвольный луч с началом в точке O.

Вдоль луча от точки O делаем n шагов равной длины, делая засечку на каждом шагу.

Последнюю засечку соединяем прямой m с точкой X.

Через остальные засечки проводим прямые, параллельные m. Эти прямые делят отрезок OX на n равных частей.

Построение параллельных прямых: Пусть по двум сторонам угла, начиная от вершины, прошлись равномерным шагом два разных существа, оставляя точечные следы. Тогда все прямые, соединяющие следы с одинаковым порядковым номером, параллельны между собой.

Задачи

4.5.1. Дана геометрическая конструкция:

4.5.2. Рассмотрим ту же геометрическую конструкцию:

Содержание

Теорема Фалеса: формулировка и пример решения задачи
Формулировка теоремы
Обобщенная формулировка
Обратная теорема Фалеса
Пример задачи
Как разделить отрезок на равные части — формулы и способы
Два одинаковых значения
Получение четырех частей
Разложение при помощи циркуля
Теорема Фалеса
🔥 Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Теорема Фалеса: формулировка и пример решения задачи

В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Формулировка теоремы

Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.

Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.

Обобщенная формулировка

Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.

В соответствии с этим для нашего чертежа выше справедливо следующее равенство:

* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.

Обратная теорема Фалеса

1. Для пересекающихся секущих

Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.

Из обратной теоремы следует:

Обязательное условие: равные отрезки должны начинаться от вершины.

2. Для параллельных секущих

Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.

Видео:Деление отрезка на равные части, перпендикуляр к прямой.Урок 4.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Пример задачи

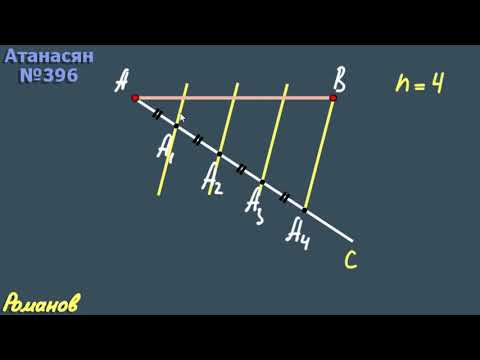
Дан отрезок AB на плоскости. Разделите его на 3 равные части.

Решение

Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.

Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.

Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).

Видео:ДЕЛЕНИЕ ОТРЕЗКА НА РАВНЫЕ ЧАСТИСкачать

Как разделить отрезок на равные части — формулы и способы

С одной стороны, разделить отрезок на равные части несложно, но с другой стороны, при этом могут появиться и трудности. Разбить какой-либо промежуток на равные части требуется не только для решения задач по геометрии, но и во многих областях жизни. В бытовой ситуации, например, такое деление может потребоваться для того, чтобы повесить картину на стене или установить мебельный гарнитур в определённой части комнаты.

Видео:Теорема Фалеса. 8 класс.Скачать

Два одинаковых значения

Самый простой способ разделить на две равнозначные доли — воспользоваться линейкой. Необходимо отмерить общую длину от точки А до точки В и разделить это значение на два. Полученное число следует отметить на заданном интервале, совместив отметку 0 на линейке с точкой А.

При делении на две идентичные доли можно воспользоваться циркулем. Для начала надо отмерить расстояние, которое будет несколько больше, чем предполагаемая половина исходной линии. Чертим две окружности, радиус которых мы определили циркулем. Одну окружность проводим из точки А, а другую — из В. Обе эти окружности между собой соединяются, образуя новые точки — С и D. Потом с помощью линейки и карандаша следует провести линию, соединяющую точки C и D. В том месте, где линия пересекает отрезок, образуется точка Е, которая является центром, а соответственно и делит его пополам.

Видео:Деление отрезка на равные части. Теорема Фалеса. ЧерчениеСкачать

Получение четырех частей

В таком варианте деления можно в упрощённом виде воспользоваться линейкой. Здесь последовательно сначала отмеряется середина, то есть отрезок делится на две равные части, как указывалось выше, а затем каждый из осечённых секторов по отдельности разделяется пополам. Таким образом, получаются четыре равных отрезка.

Однако такой вариант оказывается удачным лишь на тех прямых, которые имеют целое числовое значение. Здесь следует воспользоваться циркулем.

Видео:Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать

Разложение при помощи циркуля

Как и в первом описании, при помощи черчения двух окружностей заданный отрезок следует поделить пополам. Таким образом, на прямой образуется два отрезка — АЕ и ЕВ. Далее следует совершить аналогичные действия, но уже с двумя отрезками по отдельности. То есть, взяв отрезок АЕ, провести две окружности:

одну — из точки А;
вторую — из точки Е.

И снова в местах соединения этих двух дуг нужно провести прямую линию. Тот же самый алгоритм применяется и в отношении линии ЕВ. После проведённых манипуляций отрезок будет пересечён тремя перпендикулярными прямыми, а соответственно, разделён на четыре равные части.

Видео:ДЕЛЕНИЕ ОТРЕЗКА НА РАВНЫЕ ЧАСТИ 396 Атанасян 8 классСкачать

Теорема Фалеса

Если с делением на две или четыре равные части всё более или менее понятно, то деление отрезка на n равных частей вызывает определённые трудности. Здесь приходит на помощь формула параллельных прямых, описанная в теореме Фалеса.

Суть теоремы состоит в том, что при отложении одинаковых отрезков на одной прямой и проведении через концы этих отрезков параллельных прямых, пересекающих другую прямую, то и на второй прямой будут отложены равные между собой отрезки.

Например, на определённой прямой необходимо отмерить пять одинаковых отрезков. Для начала из точки А следует провести прямую линию, которая будет направлена в сторону противоположного конца отрезка (точки В) под острым углом относительно исходной прямой. Теперь при помощи циркуля на этой линии следует отложить пять равных отрезков. Из точки, отмерившей последний отсек, следует очертить линию в точку В. Затем провести прямые, параллельные той, которая проходит через точку В. Каждая линия должна проходить через отмеченные циркулем точки. При условии, что все линии будут строго параллельны друг другу, на исходной прямой будет отложено пять равных отрезков.

Зная, как производить деление на одинаковые части, можно, например, понять, как разделить треугольник на 4 равные части или более. По указанным вариантам деления на сегменты можно производить следующие действия: