Геометрия | 5 — 9 классы
Параллельные прямые c и d пересечены прямой a.
По данным рисунка найдите угол a.
Т. к с параллельна d угол 1( угол где 123 градуса) и угол 2 ( который вертикальный с ним) вертикальны и они равны.
Следовательно угол 2 = 123 градуса.
Угол 2 и угол а однолежащие и в сумме дают 180 градусов отсюда следует, что угол а равен 180 — 123 = 57 градусов.
- Параллельные прямые c и p пересечены прямой a, угол1 = 100 градусов?
- На рисунке прямые а и в пересечены прямой с докажите что а паралельна в если : угол 1 = углу 6?
- Параллельные прямые а и б пересечены прямой с, угол 1 = 134 градуса?
- Верным является высказывание под буквой ?
- Параллельные прямые а и б пересечены прямой с, угол 1 = 134 градуса?
- Определи по данным рисунка , если ли там параллельные прямые?
- Две параллельные прямые пересечены третьей прямой, при этом получилось 8 углов, и односторонние углы относятся как 4 : 8?
- По данным рисунка Докажите что Прямые А и Б параллельны Найдите угол 1?
- На рисунке прямые a и b параллельны, угол 1 = 55°?
- На рисунке 106 прямые а и b пересечены прямой с?
- Контр. 5. Параллельные прямые
- 1. Пользуясь данными рисунка, выберите верное утверждение:
- 2. Пользуясь данными рисунка, найдите расстояние от точки $A$ [2в.: $C$] до прямой $a$ [2в.: $c$].
- 3. Две параллельные прямые пересечены третьей прямой, найдите $∠3$, если известно, что $∠1 : ∠2 = 5 : 1$ [2в.: $∠1 : ∠2 = 5 : 1$].
- 4. Пользуясь данными рисунка, найдите угол $x.$
- 5. При пересечении двух параллельных прямых третьей один из углов оказался равным $112°$ [2в.: $74°$]. Найдите наименьший [2в.: наибольший] из всех образовавшихся при этом углов.
- 7. Прямые $b$ и $a$ не имеют общих точек. На прямой $b$ отложен отрезок $MK = 81$ см [2в.: $29$ см]. На прямой $a$ отмечена точка $E$ [2в.: $P$] так, что отрезок $KE$ [2в.: $MP$] перпендикулярен прямой $a$ [2в.: $b$] и $∠KEM = 45°$ [2в.: $∠KPM=45°$]. Найдите расстояние между прямыми $b$ и $a.$
- 8. Дан угол $ABC,$ равный $76°.$ Через точку $A$ проведена прямая, параллельная прямой $BC$ и пересекающая биссектрису угла $ABC$ в точке $M.$ Найдите углы треугольника $ABM.$
- 9. В равнобедренном треугольнике $BCK$ с основанием $BK$ угол при вершине $C$ равен $150°,$ а сторона $CK$ равна $12$ см. Найдите расстояние от точки $B$ до прямой $KC.$
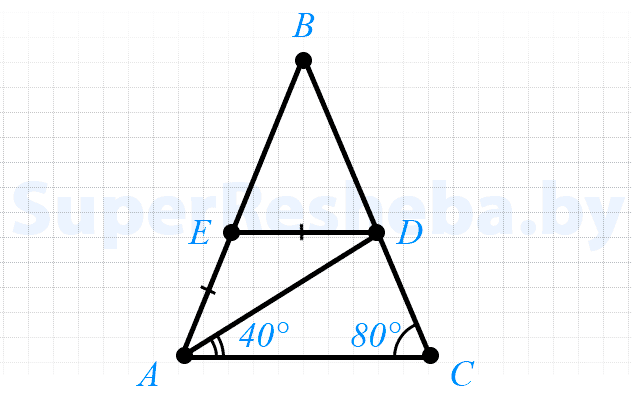
- 10. Треугольник $ABC,$ изображённый на рисунке, является равнобедренным с основанием $AC.$ Известно, что $ED = AE, ∠C = 80°,$ $∠DAC = 40°.$ Докажите, что прямые $ED$ и $AC$ параллельны. Найдите угол $BED.$
- Параллельные прямые c и d пересечены прямой a по данным рисункам найдите угол a
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямые c и p пересечены прямой a, угол1 = 100 градусов?
Параллельные прямые c и p пересечены прямой a, угол1 = 100 градусов.
Видео:№209. На рисунке 118 a||b, c||d, ∠4=45°. Найдите углы 1, 2 и 3.Скачать

На рисунке прямые а и в пересечены прямой с докажите что а паралельна в если : угол 1 = углу 6?
На рисунке прямые а и в пересечены прямой с докажите что а паралельна в если : угол 1 = углу 6.
Видео:№186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что a||b, если: a)∠1=37°Скачать

Параллельные прямые а и б пересечены прямой с, угол 1 = 134 градуса?
Параллельные прямые а и б пересечены прямой с, угол 1 = 134 градуса.
Видео:№557. Стороны угла А пересечены параллельными прямыми ВС и DE, причем точки В и D лежатСкачать

Верным является высказывание под буквой ?
Верным является высказывание под буквой .
А)если прямая пересекает одну из параллельных прямых секущей односторонние углы равны , то прямые параллельные .
Б) если прямая пересекает одну из параллельных прямых, то она перпендикулярно другой ;
в) если две параллельные прямые пересечены секущей то соответственные углы равны ;
Г) если две параллельные прямые пересечены секущей то односторонние углы равны .
Видео:№211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисыСкачать

Параллельные прямые а и б пересечены прямой с, угол 1 = 134 градуса?
Параллельные прямые а и б пересечены прямой с, угол 1 = 134 градуса.
Видео:№202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать
Определи по данным рисунка , если ли там параллельные прямые?
Определи по данным рисунка , если ли там параллельные прямые?
Видео:№205. По данным рисунка 117 найдите ∠1.Скачать

Две параллельные прямые пересечены третьей прямой, при этом получилось 8 углов, и односторонние углы относятся как 4 : 8?
Две параллельные прямые пересечены третьей прямой, при этом получилось 8 углов, и односторонние углы относятся как 4 : 8.
Найдите полученные углы (пожалуйста с рисунком).
Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

По данным рисунка Докажите что Прямые А и Б параллельны Найдите угол 1?
По данным рисунка Докажите что Прямые А и Б параллельны Найдите угол 1.
Видео:№ 186 - Геометрия 7-9 класс АтанасянСкачать

На рисунке прямые a и b параллельны, угол 1 = 55°?
На рисунке прямые a и b параллельны, угол 1 = 55°.
Видео:№ 216 - Геометрия 7-9 класс АтанасянСкачать

На рисунке 106 прямые а и b пересечены прямой с?
На рисунке 106 прямые а и b пересечены прямой с.
Докажите, что а||b.
Б) угол 1 = углу 6.
Вопрос Параллельные прямые c и d пересечены прямой a?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Это Пифагоров треугольник и гипотенуза АВ = 5. А можно и по простому — по Пифагору АВ = √(АС² + ВС²) = √(9 + 16) = 5. Ответ : АВ = 5.
AB = BK (так как АК — биссектриса)Pabk = 2AB + AK. Pakcd = AD + DC + KC + AK = BC + AB + KC + AK = AB + KC + AB + KC + AK = = 2AB + 2KC + AK. Pakcd — Pabk = 2KC = 20 (дано), отсюда КС = 10. АВ + ВС = Рabcd / 2 = 80 или 2АВ + КС = 40. Отсюда АВ = ..
Этот вид четырехугольника : параллелограмм.
Так как в треугольнике сумма двух сторон должна быть больше длины третьей стороны, то третья сторона 4 равна быть не может, значит 9.
Квадрат и треугольник.
Второй угол — 126 градусов. Угол будет равен 126 делим на 2 = 63 градуса.
Задание № 6 : В прямоугольный треугольник ABC с прямым углом A и катетами AB = 2, AC = 6 вписан квадрат ADEF. Найдите отношение площади треугольника EFC к площади квадрата ADEF. РЕШЕНИЕ : Пусть сторона квадрата х. Тогда FC = (6 — x). Площадь треу..
Sб = 2ПtH (h вторая сторона. Её нужно узнать) Подставляем : 100 = 2 * 5 * П * H H = 100 / 2 * 5П H = 100 / 10 H = 10 S(прямоугольника) = 10 * 5 = 50см ^ 2 Вроде так)).
Визначимо периметр в частинах 2( 9 + 5 ) = 28 Це і є 112 см по довжині. Тепер 112 : 28 = 4 см — довжина однієї частини. Визначаємо довжину сторін : 4 х 9 = 36 см Друга сторона 4 х 5 = 20 см Тепер перевірка за периметром : 36 + 36 + 20 + 20 = 112 см..
Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника. Диагонали, проведенные через центр основания данной пирамиды, делят его на 6 правильных треугольн..
Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Контр. 5. Параллельные прямые
Видео:№187. По данным рисунка 107 докажите, что AB||DE.Скачать

1. Пользуясь данными рисунка, выберите верное утверждение:
- а) углы $1$ и $2$ являются накрестлежащими;
- б) углы $1$ и $2$ являются односторонними;
- в) углы $1$ и $2$ являются соответственными;
- г) углы $1$ и $2$ являются вертикальными.
- а) углы $1$ и $2$ являются накрестлежащими;
- б) углы $1$ и $2$ являются односторонними;
- в) углы $1$ и $2$ являются соответственными;
- г) углы $1$ и $2$ являются вертикальными.
Видео:№ 215 - Геометрия 7-9 класс АтанасянСкачать

2. Пользуясь данными рисунка, найдите расстояние от точки $A$ [2в.: $C$] до прямой $a$ [2в.: $c$].
$AH = 4$ ($AH$ — расстояние от точки до прямой, т. к. является перпендикуляром между ними).
$CH = 12$ ($CH$ — расстояние от точки до прямой, т. к. является перпендикуляром).
Видео:№200. На рисунке 115 AD||p и PQ||BC. Докажите, что прямая р пересекает прямые АВ, АЕ, АС, ВС и PQ.Скачать

3. Две параллельные прямые пересечены третьей прямой, найдите $∠3$, если известно, что $∠1 : ∠2 = 5 : 1$ [2в.: $∠1 : ∠2 = 5 : 1$].
$∠2 = 180° : 6$ (т. к. при параллельных прямых сумма односторонних углов равна $180°$). $∠2$ и $∠3$ — вертикальные, значит $∠3 = ∠2 = 30°.$
$∠2 = 180° : 9 · 2 = 40°$ (т. к. при параллельных прямых сумма односторонних углов равна $180°$). $∠2$ и $∠3$ — накрест лежащие, значит $∠3 = ∠2 = 40°.$
Видео:ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

4. Пользуясь данными рисунка, найдите угол $x.$
Т. к. накрест лежащие углы равны, то прямые параллельны, а соответственные углы при параллельных прямых также равны, значит $∠x = 137°.$
Соответственные углы равны, значит прямые являются параллельными. Накрест лежащие углы при параллельных прямых также равны, значит $∠x = 53°.$
Видео:№558. Прямые а и b пересечены параллельными прямыми АА1, BB1, CC1, причем точки А, В и ССкачать

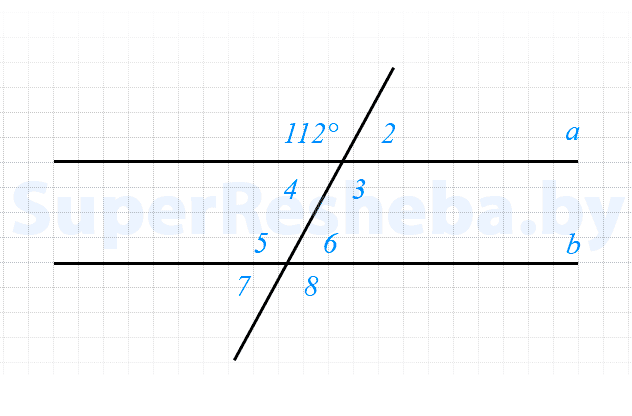
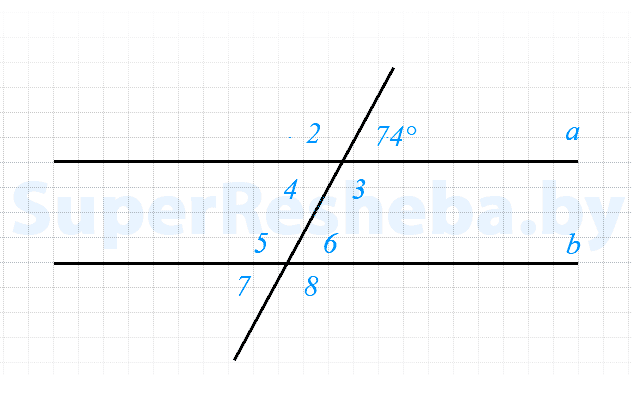
5. При пересечении двух параллельных прямых третьей один из углов оказался равным $112°$ [2в.: $74°$]. Найдите наименьший [2в.: наибольший] из всех образовавшихся при этом углов.
На рисунке $∠1 = 43°,$ а $∠2 = 137°.$ Найдите угол $∠4$, если он больше $∠3$ на $24°.$
- $∠5 = ∠2 = 137°;$
- $∠1 + ∠5 = 43° + 137° = 180°,$ значит $a || b;$
- $∠6 = ∠3,$ а $∠6$ и $∠4$ — односторонние при параллельных прямых, тогда;
$∠4 + ∠6 = ∠4 + ∠3 = 180°,$ т. е. $∠3 + 24° + ∠3 = 180°,$ из этого следует, что $2 · ∠3 = 156°; ∠3 = dfrac= 78°;$ - $∠4 = ∠3 + 24° = 78° + 24° = 102°.$
На рисунке $∠3 = 47°,$ а $∠4 = 133°.$ Найдите угол $∠1$, если он меньше $∠2$ на $58°.$
- $∠7 = ∠3 = 47°,$ $∠4 + ∠7 = 47° + 133° = 180,$ значит $a || b;$
- $∠5 = ∠2,$ а $∠5$ и $∠1$ — односторонние при параллельных прямых, тогда;
$∠1 + ∠5 = ∠1 + ∠2 = 180°,$ т. е. $∠2 — 58° + ∠2 = 180°,$ $2 · ∠2 — 58° = 180°,$ $∠2 = 119°;$ - $∠1 = 180° -∠2 = 61°.$
Видео:Параллельные прямые (задачи).Скачать

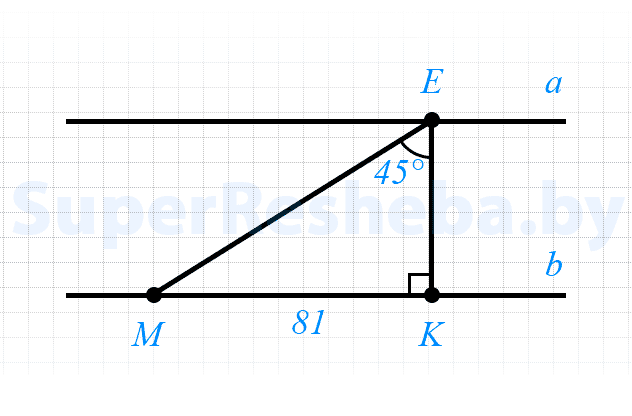
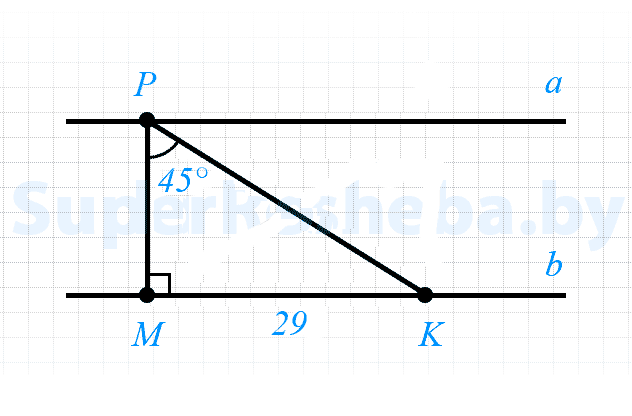
7. Прямые $b$ и $a$ не имеют общих точек. На прямой $b$ отложен отрезок $MK = 81$ см [2в.: $29$ см]. На прямой $a$ отмечена точка $E$ [2в.: $P$] так, что отрезок $KE$ [2в.: $MP$] перпендикулярен прямой $a$ [2в.: $b$] и $∠KEM = 45°$ [2в.: $∠KPM=45°$]. Найдите расстояние между прямыми $b$ и $a.$
- $a$ и $b$ не имеют общих точек, значит $a || b;$
- $EK ⊥ a,$ значит $EK ⊥ b;$
- $∠EMK = 180° — (90° + 45°) = 45°,$ значит $ΔEMK$ — равнобедренный, $EK = MK = 81$ см.
- $a$ и $b$ не имеют общих точек, значит $a || b;$
- $PK ⊥ a,$ значит $PK ⊥ b;$
- $∠PMK = 180° — (90° + 45°) = 45°,$ значит $ΔPMK$ — равнобедренный, $PM = MK = 29$ см.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

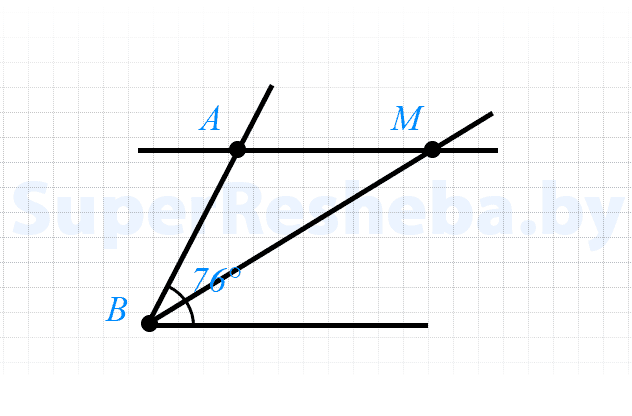
8. Дан угол $ABC,$ равный $76°.$ Через точку $A$ проведена прямая, параллельная прямой $BC$ и пересекающая биссектрису угла $ABC$ в точке $M.$ Найдите углы треугольника $ABM.$
- $∠MAB$ и $∠ABC$ — односторонние, значит $∠MAB = 180° — 76° = 104°;$
- $∠ABM = 76° : 2 = 38°,$ т. к. биссектриса делит угол пополам;
- $∠BMA = 180° — (104° + 38°) = 38°.$
Ответ: $104°, 38°, 38°.$
Видео:Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

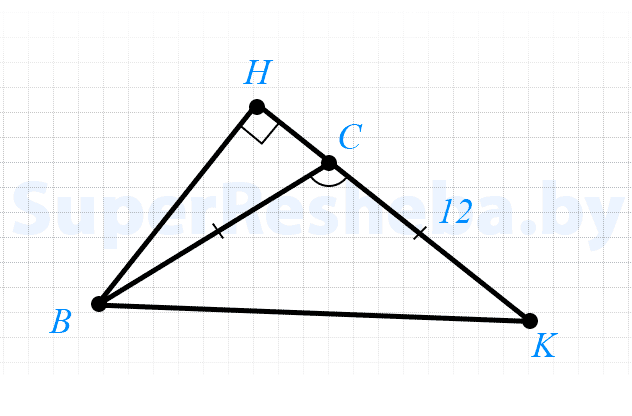
9. В равнобедренном треугольнике $BCK$ с основанием $BK$ угол при вершине $C$ равен $150°,$ а сторона $CK$ равна $12$ см. Найдите расстояние от точки $B$ до прямой $KC.$
- $ΔBCK$ — равнобедренный, значит $CB = CK = 12$ см;
- $∠HCB$ и $∠KCB$ — смежные, значит $∠HCB = 180° — 150° = 30°;$
- $ΔHCB$ — прямоугольный, а $∠HCB = 30°,$ то $BH = dfrac· BC = dfrac· 12 = 6$ см.
Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

10. Треугольник $ABC,$ изображённый на рисунке, является равнобедренным с основанием $AC.$ Известно, что $ED = AE, ∠C = 80°,$ $∠DAC = 40°.$ Докажите, что прямые $ED$ и $AC$ параллельны. Найдите угол $BED.$
- $ΔABC$ — равнобедренный, значит $∠C = ∠A,$ тогда $∠EAD = 80° — ∠DAC$ $= 80° — 40° = 40°;$
- $ΔEDA$ — равнобедренный, значит $∠EAD = ∠EDA = 40°;$
- $∠EAD$ и $∠EDA$ — накрест лежащие, значит $ED || AC.$
Параллельные прямые c и d пересечены прямой a по данным рисункам найдите угол a
305. Параллельны ли изображённые на рисунке 212 прямые a и b , если:
3) ∠ 4 = 125°, ∠ 6 = 55°;
4) ∠ 2 = 35°, ∠ 5 = 146°;
5) ∠ 1 = 98°, ∠ 6 = 82°;
6) ∠ 1 = 143°, ∠ 7 = 37°?
306. На каких из рисунков 213, а – г прямые m и n параллельны?
307. На рисунке 214 укажите все пары параллельных прямых.
308. На рисунке 215 укажите параллельные прямые, если ∠ 1 = 53°, ∠ 2 = 128°, ∠ 3 = 127°.
309. На рисунке 216 AB = BC , CD = DK . Докажите, что AB ‖ DK .
310. На рисунке 217 AK — биссектриса угла BAC , AM = MK . Докажите, что MK ‖ AC .
311. На рисунке 218 ∠ ACB = ∠ ACD , AD = CD . Докажите, что BC ‖ AD .
312. В треугольнике ABC известно, что AB = BC , ∠ A = 60°, ∠ BCD — смежный с ∠ ACB , CM — биссектриса угла BCD . Докажите, что AB ‖ CM .
313. Отрезки AB и CD пересекаются в точке O и делятся этой точкой пополам. Докажите, что AC ‖ BD .
314. На рисунке 219 AB = CD , BC = AD . Докажите, что AB ‖ CD .
315. Известно, что некоторая прямая m пересекает прямую a (рис. 220). Пересекает ли прямая m прямую b ?
316. Каково взаимное расположение прямых CD и EF на рисунке 221?
317. Угол ABC равен 60°, а угол BCD — 120°. Можно ли утверждать, что прямые AB и CD параллельны?
318. Угол между прямыми a и c равен углу между прямыми b и c . Можно ли утверждать, что прямые a и b параллельны?
319. Четыре угла, образованные при пересечении прямых a и b прямой c , равны по 40°, а любой из остальных четырёх углов — 140°. Можно ли утверждать, что прямые a и b параллельны?
320. Прямая пересекает биссектрису BM треугольника ABC в точке O , являющейся серединой отрезка BM , а сторону BC — в точке K . Докажите, что если OK ⊥ BM , то MK ‖ AB .
321. Отрезки AM и CK — медианы треугольника ABC . На продолжении отрезка AM за точку M отложен отрезок MF , а на продолжении отрезка CK за точку K — отрезок KD так, что MF = AM , KD = CK . Докажите, что точки B , D и F лежат на одной прямой.
Упражнения для повторения
322. Луч OC разбивает угол AOB на два угла так, что ∠ AOC : ∠ BOC = 3 : 5. Найдите угол между лучом OC и биссектрисой угла, смежного с углом AOB , если угол BOC на 42° больше угла AOC .
323. На рисунке 222 AB = BC , ∠ ABK = ∠ CBM . Докажите, что BM = BK .
324. Равнобедренные треугольники ABC и ADC имеют общее основание AC . Прямая BD пересекает отрезок AC в точке E . Докажите, что AE = EC .
Наблюдайте, рисуйте, конструируйте, фантазируйте
325. Приведите пример, когда общей частью (пересечением) треугольника и четырёхугольника является восьмиугольник.
Когда сделаны уроки
Пятый постулат Евклида
В § 6 вы узнали, что в качестве аксиом выбирают очевидные утверждения. Тогда почему бы, например, теоремы 1.1 и 5.1 не включить в список аксиом, ведь они тоже очевидны? Ответ на этот вопрос понятен: если какое-то утверждение можно доказать с помощью аксиом, то это утверждение — теорема, а не аксиома. С этих позиций очень поучительна история, связанная с пятым постулатом Евклида
V постулат. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны от секущей, с которой эта сумма меньше двух прямых углов ( рис. 223 ).
Можно показать, что пятый постулат и сформулированная нами в § 13 аксиома параллельности прямых равносильны, т. е. из постулата следует аксиома и наоборот — из аксиомы следует постулат.
Более двадцати веков многие учёные пытались доказать пятый постулат, т. е. вывести его из других аксиом Евклида. Лишь в начале XIX в. несколько математиков независимо друг от друга пришли к выводу: утверждение, что через данную точку, не лежащую на данной прямой, мож но провести только одну прямую, параллельную данной , является аксиомой.
Вам может показаться, что в этом выводе ничего особенного нет: присоединяем аксиому параллельности к уже существующему списку аксиом-правил, а дальше доказываем теоремы.
Однако если в футболе добавить только одно правило, например разрешить полевым игрокам играть и руками, то мы получим совершенно новую игру.
Если пятый постулат — это правило, которое мы принимаем, а не теорема, то его можно заменить противоположным утверждением.
Так и поступил Н.И. Лобачевский. Он заменил лишь одно правило — аксиому параллельности прямых — следующим: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную. Новая аксиома позволила построить новую геометрию — неевклидову.
Н.И. Лобачевский (1792–1856)
Выдающийся русский математик, про-
фессор Казанского университета.
С подобной идеей несколько позже выступил венгерский математик Янош Бойяи (1802–1860).