Отрицательная окружность по тригонометрии

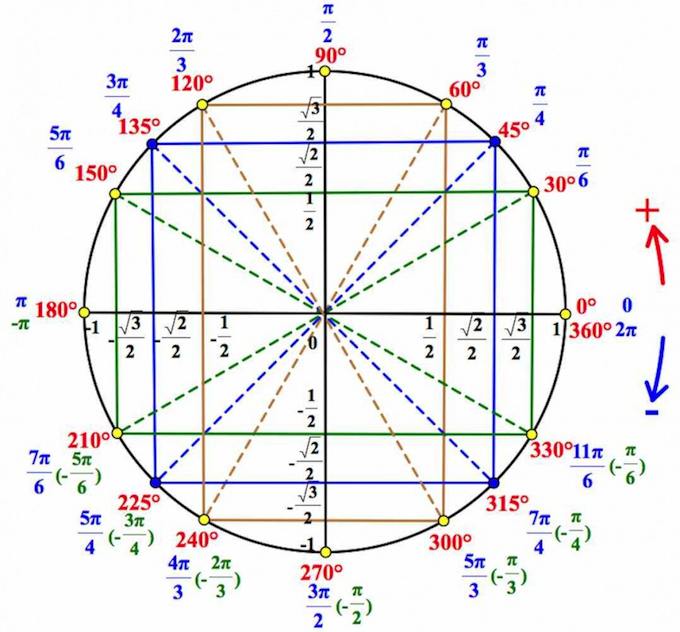
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг :

Мы же здесь будем все подробно разбирать шаг за шагом + показать

Тригонометрический круг – не роскошь, а необходимость

Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…

Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.

Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!

Нас выручит тригонометрический круг ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!

К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, градусов, или .

Никак. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!

А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.

Знакомство с тригонометрическим кругом

Давайте по порядку.

Сначала выпишем вот такой ряд чисел:

И, наконец, такой:

Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .

Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».

И зачем оно нам?

Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.

Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).

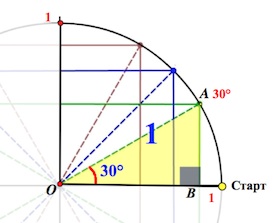
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .

Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.

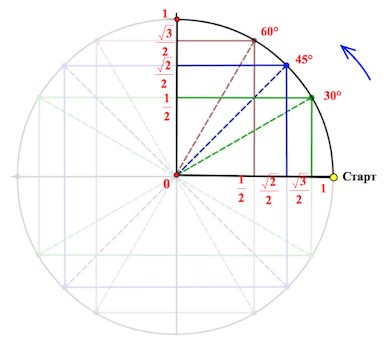
Это почему же, спросите вы?

Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.

Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть ).

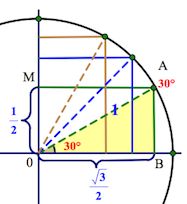
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора

Надеюсь, уже что-то становится понятно?

Так вот точка В и будет соответствовать значению , а точка М – значению

Аналогично с остальными значениями первой четверти.

Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . Про тангенс и котангенс позже.

Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.

Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг , без которого никуда в тригонометрии.

А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:10 класс, 11 урок, Числовая окружностьСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Видео:Тригонометрическая окружность. Как выучить?Скачать

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:

• Синус угла – отношение противолежащего катета к гипотенузе;
• Косинус угла – отношение прилежащего катета к гипотенузе;
• Тангенс угла – отношение противолежащего катета к прилежащему;
• Котангенс угла – отношение прилежащего катета к противолежащему.

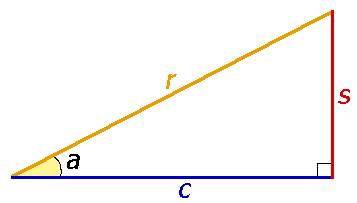
Или в виде формул:

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

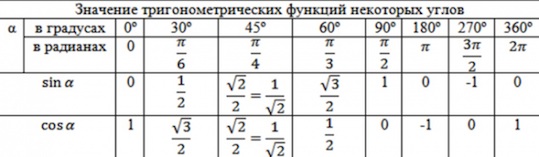
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

0°	30°	45°	60°	90°
sin	0	1	√3	–
ctg	–	√3	1	Принцип повтора знаков тригонометрических функций Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать Тригонометрический круг Углы в радианах Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. 💡 Видео Как искать точки на тригонометрической окружности.Скачать Отрицательный аргумент у тригонометрических функций [понять нельзя заучивать]Скачать Тригонометрическая окружность для непонимающихСкачать 🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать Четность, нечетность тригонометрических функций. 9 класс.Скачать Знаки тригонометрических функций. 9 класс.Скачать ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэ #окружностьСкачать Радианная мера угла. 9 класс.Скачать Отбор корней по окружностиСкачать Тригонометрический круг вместо стопки формулСкачать Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать Найти знак тригонометрической функции (bezbotvy)Скачать 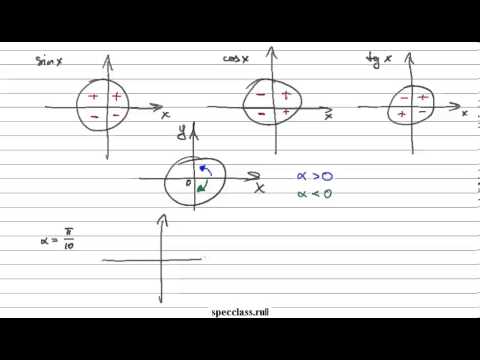Тригонометрические функции и их знакиСкачать Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности