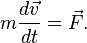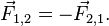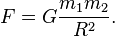Физика > Сила в двух измерениях
Силы действуют в определенном направлении и характеризуются размерами, зависящими от того, насколько сильным был толчок или тяга.
- Задача обучения
- Основные пункты
- Термины
- —>Физика —>
- 2.Первый закон Ньютона.
- 3.Второй закон Ньютона.
- 4.Третий закон Ньютона.
- 5.Гравитация.
- 6.Электростатическое поле (поле неподвижных зарядов).
- 7.Электромагнитное поле (поле постоянных токов).
- 8.Сильное взаимодействие.
- Вектор силы (Определение, Пример)
- ЧТО ТАКОЕ ВЕКТОР СИЛЫ
- Опыт по определению вектора силы
- Равновесие сил
- Равновесие трех сил, треугольник сил
- Похожие страницы:
- 📸 Видео
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Задача обучения
- Объяснить, почему силы классифицируются как векторные величины.
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Основные пункты
- При вычислении результата двух действующих сил, нужно знать величину и направление обоих.
- Чтобы определить общую силу от двух действующих, необходимо воспользоваться правилом параллелограмма сложение векторов.
- Диаграммы свободного тела выступают удобным способом отслеживания действующих сил.
Видео:Физика | Ликбез по векторамСкачать

Термины
- Результирующий – вектор, выступающий векторной суммой квадратных векторов.
- Диаграмма свободного тела – графическое изображение действующих сил.
- Вектор – направленное количество, обладающее величиной и направлением (между двумя точками).
Силы действуют в определенном направлении и обладают размером, зависящем от силы, приложенной к толчку или тяге. Это векторные силы. Чтобы определить результат действия двух сил, нужно знать их величины и направление. Например, два человека тянут за веревку с известной силой, но в неизвестных направлениях. Они могут отображать перетягивание каната или тянуть вместе. Если мы не узнаем, то остается неясным, что делать дальше: суммировать или вычитать.
Диаграммы свободного тела объекта на наклонной плоскости
Когда две силы воздействуют на точечную частичку, то результирующая сила (чистая) определяется правилом параллелограмма сложения векторов: добавление двух векторов, отображенных сторонами параллелограмма, дают эквивалентный результирующий вектор. Его величина зависит от разности величин двух сил.
Можно также использовать диаграммы (график) свободного тела. Их отображают с учетом углов и относительных величин векторов силы.
Видео:Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать

—>Физика —>
1.Си́ла — векторная физическая величина , являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей . Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений .
Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе ввекторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы).
Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.
Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с равнодействующей всех сил, приложенных к телу, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, скорость изменения импульса материальной точки равна приложенной силе.
При приложении силы к телу конечных размеров в нём возникают механические напряжения, сопровождающиеся деформациями.
С точки зрения Стандартной модели физики элементарных частиц фундаментальные взаимодействия (гравитационное, слабое, электромагнитное, сильное) осуществляются посредством обмена так называемыми калибровочными бозонами. Эксперименты по физике высоких энергий, проведённые в 70−80-х гг. XX в. подтвердили предположение о том, что слабое и электромагнитное взаимодействия являются проявлениями более фундаментального электрослабого взаимодействия [8] .
Размерность силы — LMT −2 , единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС — дина.
2.Первый закон Ньютона.
Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий. Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой физически неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении», а какие «покоятся». Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.
3.Второй закон Ньютона.
Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку.
где 
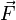
По определению импульса:
где 
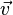
В классической механике при скоростях движения много меньше скорости света масса материальной точки считается неизменной, что позволяет выносить её при этих условиях за знак дифференциала :
Учитывая определение ускорения точки, второй закон Ньютона принимает вид:
Считается, что это «вторая самая известная формула в физике», хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде. Впервые данную форму закона можно встретить в трудах К.Маклорена иЛ.Эйлера.
Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, то и сила инвариантна по отношению к такому переходу.
Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратное утверждение, т.е установление факта такого движения, не свидетельствует об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю. На этом основано измерение величины силы, когда она компенсируется силой, величина которой известна .
Второй закон Ньютона позволяет измерять величину силы. Например, знание массы планеты и ее центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующую на эту планету со стороны Солнца.
4.Третий закон Ньютона.
Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2 сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2. Математически закон записывается так:
Этот закон означает, что силы всегда возникают парами «действие-противодействие». Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел равна нулю:
Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.
5.Гравитация.
Гравитация (сила тяготения) — универсальное взаимодействие между любыми видами материи. В рамках классической механики описывается законом всемирного тяготения, сформулированным Исааком Ньютоном в его труде «Математические начала натуральной философии». Ньютон получил величину ускорения, с которым Луна движется вокруг Земли, положив при расчете, что сила тяготения убывает обратно пропорционально квадрату расстояния от тяготеющего тела. Кроме этого, им же было установлено, что ускорение, обусловленное притяжением одного тела другим, пропорционально произведению масс этих тел. На основании этих двух выводов был сформулирован закон тяготения: любые материальные частицы притягиваются по направлению друг к другу с силой 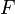
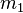
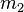

Здесь 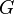
Более общей теорией гравитации является общая теория относительности Альберта Эйнштейна. В ней гравитация не характеризуется инвариантной силой, не зависящей от системы отсчёта. Вместо этого свободное движение тел в гравитационном поле, воспринимаемое наблюдателем как движение по искривленным траекториям в трехмерном пространстве-времени с переменной скоростью, рассматривается как движение по инерции по геодезической линии в искривлённом четырехмерном пространстве-времени, в котором время в разных точках течет по-разному. Причем эта линия в некотором смысле «наиболее прямая» — она такова, что пространственно-временной промежуток (собственное время) между двумя пространственно-временными положениями данного тела максимален. Искривление пространства зависит от массы тел, а также от всех видов энергии, присутствующих в системе.
6.Электростатическое поле (поле неподвижных зарядов).
Развитие физики после Ньютона добавило к трём основным (длина, масса, время) величинам электрический заряд с размерностью C. Однако, исходя из требований практики, в качестве основной единицы измерения стали использовать не единицу заряда, а единицу силы электрического тока. Так, в системе СИ основной единицей является ампер, а единица заряда — кулон — производная от него.
Поскольку заряд, как таковой, не существует независимо от несущего его тела, то электрическое взаимодействие тел проявляется в виде той же рассматриваемой в механике силы, служащей причиной ускорения. Применительно к электростатическому взаимодействию двух точечных зарядов величинами 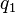
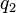
где 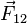
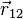

Сила направлена вдоль линии, соединяющей точечные заряды. Графически электростатическое поле принято изображать в виде картины силовых линий, представляющих собой воображаемые траектории, по которым бы перемещалась лишённая массы заряженная частица. Эти линии начинаются на одном и заканчиваются на другом заряде.
7.Электромагнитное поле (поле постоянных токов).
Существование магнитного поля признавалось ещё в средние века китайцами, использовавшим «любящий камень» — магнит, в качестве прообраза магнитного компаса. Графически магнитное поле принято изображать в виде замкнутых силовых линий, густота которых (так же, как и в случае электростатического поля) определяет его интенсивность. Исторически наглядным способом визуализации магнитного поля были железные опилки, насыпаемые, например, на лист бумаги, положенный на магнит.
Эрстед установил, что текущий по проводнику ток вызывает отклонение магнитной стрелки.
Фарадей пришёл к выводу, что вокруг проводника с током создаётся магнитное поле.
Ампер высказал гипотезу, признаваемую в физике, как модель процесса возникновения магнитного поля, заключающуюся в существовании в материалах микроскопических замкнутых токов, обеспечивающих совместно эффект естественного или наведённого магнетизма.
Ампером было установлено, что в находящейся в вакууме системе отсчёта, по отношению к которой заряд находится в движении, то есть ведёт себя как электрический ток, возникает магнитное поле, интенсивность которого определяется вектором магнитной индукции
Единицей измерения магнитной индукции является тесла: 1 Тл = 1 Т кг с −2 А −2
Количественно задача была решена Ампером, измерявшим силу взаимодействия двух параллельных проводников с текущими по ним токами. Один из проводников создавал вокруг себя магнитное поле, второй реагировал на это поле сближением или удалением с поддающейся измерению силой, зная которую и величину силы тока можно было определить модуль вектора магнитной индукции.
Силовое взаимодействие между электрическими зарядами, не находящимися в движении относительно друг друга описывается законом Кулона. Однако заряды, находящиеся в движении относительно друг друга создают магнитные поля, посредством которых созданные движением зарядов токов в общем случае приходят в состояние силового взаимодействия.
Принципиальным отличием силы, возникающей при относительном движении зарядов от случая их стационарного размещения, является различие в геометрии этих сил. Для случая электростатики сил взаимодействия двух зарядов направлена по линии, их соединяющей. Поэтому геометрия задачи двумерна и рассмотрение ведётся в плоскости, проходящей через эту линию.
В случае токов сила, характеризующая магнитное поле, создаваемое током, расположена в плоскости, перпендикулярной току. Поэтому картина явления становится трёхмерной. Магнитное поле, создаваемое бесконечно малым по длине элементом первого тока, взаимодействуя с таким же элементом второго тока, в общем случае создаёт силу, действующую на него. При этом для обоих токов эта картина полностью симметрична в том смысле, что нумерация токов произвольна.
Закон взаимодействия токов используется для эталонирования постоянного электрического тока.
8.Сильное взаимодействие.
Сильное взаимодействие — фундаментальное короткодействующее взаимодействие между адронами и кварками. В атомном ядре сильное взаимодействие удерживает вместе положительно заряженные (испытывающие электростатическое отталкивание) протоны, происходит это посредством обмена пи-мезонами между нуклонами (протонами и нейтронами). Пи-мезоны живут очень мало, времени жизни им хватает лишь на то, чтобы обеспечить ядерные силы в радиусе ядра, потому ядерные силы называют короткодействующими. Увеличение количества нейтронов «разбавляет» ядро, уменьшая электростатические силы и увеличивая ядерные, но при большом количестве нейтронов они сами, будучи фермионами, начинают испытывать отталкивание вследствие принципа Паули. Также при слишком сильном сближении нуклонов начинается обмен W-бозонами, вызывающее отталкивание, благодаря этому атомные ядра не «схлопываются».
Внутри самих адронов сильное взаимодействие удерживает вместе кварки — составные части адронов. Квантами сильного поля являются глюоны. Каждый кварк имеет один из трёх «цветовых» зарядов, каждый глюон состоит из пары «цвет»-«антицвет». Глюоны связывают кварки в т. н. «конфайнмент», из-за которого на данный момент свободные кварки в эксперименте не наблюдались. При отдалении кварков друг от друга энергия глюонных связей возрастает, а не уменьшается как при ядерном взаимодействии. Затратив много энергии (столкнув адроны в ускорителе) можно разорвать кварк-глюонную связь, но при этом происходит выброс струи новых адронов. Впрочем, свободные кварки могут существовать в космосе: если какому-то кварку удалось избежать конфайнмента во время Большого взрыва, то вероятность аннигилировать с соответствующим антикварком или превратиться в бесцветный адрон для такого кварка исчезающе мала.
Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Вектор силы (Определение, Пример)
Видео:Урок 270. Магнитное поле и его характеристикиСкачать

ЧТО ТАКОЕ ВЕКТОР СИЛЫ

При сооружении и проектировании мостов, зданий, кранов, машин инженеров очень заботит сложение сил или же разность сил для определения силы, необходимой для достижения равновесия. Можно показать, что силы — это векторы, т. е. они подчиняются правилу геометрического сложения.
Векторному сложению и разложению уравновешенных сил посвящен раздел физики, называемый «статикой». Это большой, но скучный раздел физики, и большинство учебников уделяет ему много места, излагая приемы решения задач инженерной статики. Мы ограничимся лишь несколькими примерами, и даже их, пожалуй, лучше было бы опустить, чтобы уделить больше времени изучению силы и движения.
Прежде всего мы должны удостовериться в том, что силы — это векторы. Сказать, что они должны быть векторами, поскольку они характеризуются величиной и направлением, недостаточно. Это не убеждает нас в том, что силы складываются геометрически.
Хотя это утверждение кажется вполне правдоподобным, особенно тем, кто имеет дело с канатами и веревками на кораблях или кому приходится заниматься разбивкой палаток, мы же должны проворить его непосредственно.
Опыт по определению вектора силы

Она равна и проти воположна силе FС. Это требует дополнительного доказательства, поскольку FС не равнодействующая (сумма) двух других сил, а «равновесная» сила, необходимая, чтобы им противостоять.
Рис. Косвенная проверка векторного сложения сил.
Равновесие сил

В этом случае мы говорим, что силы находятся «в равновесии». Если сумма нескольких сил равна нулю, то это должно быть видно на диаграмме векторного сложения; длина линии, соединяющей исходную точку диаграммы с конечной, должна быть равна нулю. Это означает, что векторная диаграмма должна представлять собой замкнутую фигуру.
Таким образом, если сумма сил равна нулю, то конец векторного многоугольника должен прийти обратно к началу. Это иллюстрирует рис. 3. Условие равенства нулю равнодействующей для постоянного равновесия сил должно выполняться для всей конструкции, например для всего крана или моста, но оно должно также выполняться для каждой отдельной детали конструкции, находящейся в состоянии равновесия.
Применяя это условие к какой-нибудь определенной детали, например к стреле крана, к одной опоре моста, к заклепке, связывающей воедино несколько различных деталей моста, или к грузу маятника, нужно быть внимательным и учитывать все силы, действующие на данную деталь. Тогда мы сможем утверждать, что имеем полный набор сил, образующих замкнутую векторную диаграмму, если, конечно, деталь находится в равновесии.
При решении задач не следует включать в рассмотрение силы, приложенные к другим деталям. Сначала выберите и пометьте выбранную деталь, которая, как вы считаете, находится в равновесии.
Равновесие трех сил, треугольник сил

а — три силы в равновесии) б — три силы не находятся в равновесии.
Этим пользуются при решении инженерных задач. Во многих конструкциях на каждую деталь, играющую важную роль, действуют как раз три силы. Чтобы конструкция была устойчивей, каждая деталь должна оставаться в состоянии покоя; сумма всех действующих на нее сил должна быть равна нулю. Таким образом, если к любой детали приложены три силы, мы строим для них замкнутый треугольник.
Похожие страницы:
Понравилась статья поделись ей
📸 Видео
Построение проекции вектора на осьСкачать

Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

§4.3. Главный вектор и главный момент сил инерцииСкачать

Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Урок 32 (осн). Сила. Единицы силы. Изображение силСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ сила Ампера правило левой рукиСкачать

Урок 9. Проекции вектора на координатные осиСкачать

Как проецировать вектор сил на оси | ЕГЭ Физика | Николай Ньютон. ТехноскулСкачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Физика - Магнитное полеСкачать

Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать