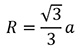Как построить призму треугольника

Видео:Как сделать объемную ТРЕУГОЛЬНУЮ ПРИЗМУ из бумаги А4? // Геометрические фигуры своими рукамиСкачать

Треугольная призма — это многогранник,две грани которого являются равными треугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.

Видео:Как начертить ПРИЗМУ ТРЕХГРАННУЮСкачать

Правильная треугольная призма — это треугольная призма у которой основания правильные треугольники (все стороны которых равны, углы между сторонами основания составляют 60 градусов), а боковые грани прямоугольники.

Основания призмы являются равными правильными треугольниками.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности треугольной призмы:

Объём призмы равен произведению её высоты на площадь основания.

Формула объема правильной треугольной призмы:

Правильная треугольная призма может быть вписана в цилиндр.

Формула радиуса цилиндра вписанной треугольной призмы:

Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.

Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.

Видео:оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How to make Paper PyramidСкачать

Треугольная призма все формулы и примеры задач

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Видео:Как сделать объемную ТРЕУГОЛЬНУЮ ПРИЗМУ из бумаги А4? / Объемные геометрические фигуры своими рукамиСкачать

Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы .

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы .

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Видео:Призма треугольная из картонаСкачать

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Видео:КАК СДЕЛАТЬ ТРЕУГОЛЬНУЮ ПРИЗМУ ИЗ БУМАГИ? ОБЪЁМНАЯ ТРЕУГОЛЬНАЯ ПРИЗМА ИЗ БУМАГИ. ПРИЗМА. | #RAIDOTVСкачать

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

Объем призмы = площадь основания х высота

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

так как S_бок=P_осн . h, то получим:

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы :

Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см 2 , то высота должна быть выражена в сантиметрах, а объем — в см 3 . Если площадь основания в мм 2 , то высота должна быть выражена в мм, а объем в мм 3 и т. д.

Видео:УРОК 3.КАК НАРИСОВАТЬ ПРИЗМУ,ПИРАМИДУ.Обучение рисунку.Урок рисования карандашом.построение поэтапноСкачать

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Видео:Развертка тетраэдра - это легко! Как сделать объёмную правильную треугольную пирамиду из бумаги?Скачать

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k 2 = S₁2 2 = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Таким образом, искомый объём равен 20.

Формулы по математике для ЕГЭ и ОГЭ

Шар и сфера, объем шара, площадь сферы, формулы

Видео:ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Как построить правильную треугольную призму

Треугольная призма является одной из частых объемных геометрических фигур, которые мы встречаем в нашей жизни. Например, в продаже можно встретить брелки и часы в форме нее. В физике эту фигуру, сделанную из стекла, используют для изучения спектра света. В данной статье освятим вопрос, касающийся развертки треугольной призмы.

Видео:Как сделать ЧЕТЫРЕХУГОЛЬНУЮ ПИРАМИДУ из бумаги? ||| Геометрические фигуры своими рукамиСкачать

Что собой представляет треугольная призма

Рассмотрим эту фигуру с геометрической точки зрения. Чтобы ее получить, следует взять треугольник, имеющий произвольные длины сторон, и параллельно самому себе перенести его в пространстве на некоторый вектор. После этого необходимо соединить одинаковые вершины исходного треугольника и треугольника, полученного переносом. Мы получили треугольную призму. Ниже фото демонстрирует один из примеров этой фигуры.

Из рисунка видно, что она образована 5-ю гранями. Две одинаковые треугольные стороны называются основаниями, три стороны, представленные параллелограммами, называются боковыми. У этой призмы можно насчитать 6 вершин и 9 ребер, из которых 6 лежат в плоскостях параллельных оснований.

Видео:Как начертить ПРИЗМУ ШЕСТИГРАННУЮ в объемеСкачать

Правильная треугольная призма

Выше была рассмотрена треугольная призма общего типа. Она будет называться правильной, если выполняются следующих два обязательных условия:

1. Ее основание должно представлять правильный треугольник, то есть все его углы и стороны должны быть одинаковыми (равносторонний).
2. Угол между каждой боковой гранью и основанием должен быть прямым, то есть составлять 90 o .

На фото выше изображена рассматриваемая фигура.

Для правильной треугольной призмы удобно выполнять расчеты длины ее диагоналей и высоты, объема и площади поверхности.

Видео:Построение призмы высотой 30ммСкачать

Развертка правильной треугольной призмы

Возьмем правильную призму, представленную на предыдущем рисунке, и проведем мысленно для нее следующие операции:

1. Разрежем сначала два ребра верхнего основания, которые ближе всего находятся к нам. Отогнем основание вверх.
2. Операции пункта 1 проделаем для нижнего основания, только отогнем его вниз.
3. Разрежем фигуру по ближайшему боковому ребру. Отогнем влево и вправо две боковые грани (два прямоугольника).

В итоге мы получим развертку треугольной призмы, которая представлена ниже.

Эту развертку удобно использовать для вычисления площади боковой поверхности и оснований фигуры. Если длина бокового ребра равна c, а длина стороны треугольника равна a, тогда для площади двух оснований можно записать формулу:

Площадь боковой поверхности будет равна трем площадям одинаковых прямоугольников, то есть:

Тогда полная площадь поверхности будет равна сумме S_o и S_b.

Главная страница » Основы Академического рисунка » Как построить призму. Правильное изображение фигуры на рисунке

Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.

В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Рисуем четырехгранную призму

Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.

Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).

Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.

Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.

Видео:КАК СДЕЛАТЬ ШЕСТИУГОЛЬНУЮ ПРИЗМУ ИЗ БУМАГИ? ОБЪЁМНАЯ ШЕСТИГРАННАЯ ПРИЗМА ИЗ БУМАГИ. | #RAIDOTVСкачать

Шестигранная призма

Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.

Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.

Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.

Видео:Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Зачем уметь строить эту геометрическую фигуру?

Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.

С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.

Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.

Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.

В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.

Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.

Основания призмы правильные треугольники (все стороны которых равны, углы между сторонами основания составляют 60 градусов).

Популярное

(головоломка «звезда») Состоит из шести симметричных брусочков сложной формы соединенных в форме многогранной звезды. Задача заключается в том, чтобы разъединить фигуру на.

Нечасто удается встретить многогранники за пределами учебников математики. И если такие геометрические формы как куб, призма и цилиндр встречаются повседневно, то.

Многогранник – (определение) геометрическое тело, ограниченное со всех сторон плоскими многоугольниками – гранями.

Знакомые каждому с детства коробочки для Биг-Мака и картошки, стаканчик для Кока-Колы так же делают из бумажных разверток.

Достаточно часто возникает вопрос о практическом применении бумажных развёрток.Какой смысл в бумажном моделировании?

АРХИМЕД (287 – 212 до н.э.) – древнегреческий математик, физик и механик. Архимед – автор многочисленных открытий и.

Сделать новогодний праздник красивым и необычным, чтобы дети видели в нём сказку, а гости восхищались, можно только своими руками. Бумажные многогранники –.

💥 Видео

Как сделать ТРЕУГОЛЬНУЮ ПИРАМИДУ из бумаги? ||| Геометрические фигуры своими рукамиСкачать

Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

КАК СДЕЛАТЬ ШЕСТИУГОЛЬНУЮ ПИРАМИДУ ИЗ БУМАГИ? ШЕСТИУГОЛЬНАЯ ПИРАМИДА. ОБЪЕМНЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать