Центральный угол окружности — это угол, образованный двумя радиусами окружности, вершина которого совпадает с центром окружности.
O — центр окружности, AO и OB — радиусы окружности, образующие два центральных угла с вершиной в центре O.
Дуга, лежащая во внутренней области угла, называется дугой, соответствующей этому центральному углу.
Углу AOB соответствует две дуги с концами A и B. Если угол AOB является развёрнутым, то он будет разделять окружность на две равные дуги, называемые полуокружностями:
∠AOB — развёрнутый угол, 

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Градусная мера дуги окружности
Дугу окружности можно измерять в градусах. Градусная мера дуги — это градусная мера соответствующего ей центрального угла.
Если дуга AB окружности с центром O меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла AOB. Если же дуга больше полуокружности, то её градусная мера считается равной 360° —∠AOB:



Сумма градусных мер двух дуг с общими концами равна 360°:


Видео:Углы, связанные с окружностьюСкачать

Углы, связанные с окружностью
 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:№661. Найдите острый угол, образованный двумя секущими, проведенными из точки, лежащейСкачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Угол между касательной и хордойСкачать
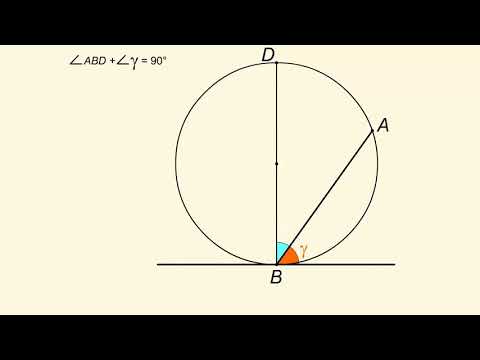
Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:8 класс. Углы в окружностиСкачать  Окружность. Центральный угол.Центральным угол – это угол образованный двумя радиусами окружности. Пример центрального угла — угол AOB, ВОС, СОЕ и так далее. О центральном угле и дуге, заключенной между его сторонами, говорят, что они соответствуют друг другу. В одном круге или в равных кругах: 1. если центральные углы равны, то и соответствующие им дуги равны. 2. если центральные углы не равны, то большему из них соответствует большая дуга. Пусть AOB и COD два центральных угла, равных или неравных. Повернем сектор AOB вокруг центра в направлении, указанном стрелкой, настолько, чтобы радиус OA совместился с OC.Тогда, если центральные углы равны, то радиус OA совпадет с OD и дуга AB с дугой СD. Значит эти дуги будут равны. Если же центральные углы не равны, то радиус OB пойдет не по OD, а по какому-нибудь иному направлению, например, по OE или по OF. В том и другом случае большему углу, очевидно, соответствует и большая дуга. Теорема, доказанная нами для одного круга, остается верной для равных кругов, потому что такие круги ничем друг от друга не отличаются, кроме своего положения. Обратные предложения так же будет верным. В одном круге или в равных кругах: 1. если дуги равны, то и соответствующие им центральные углы равны. 2. если дуги не равны, то большей из них соответствует больший центральный угол. В одном круге или в равных кругах центральные углы относятся, как соответствующие им дуги. Или перефразировав получаем, что центральный угол пропорционален соответствующей ему дуге. 🔍 ВидеоДлина дуги окружности. 9 класс.Скачать  8 класс. Геометрия. Углы, образованные хордами, секущими и касательнымиСкачать 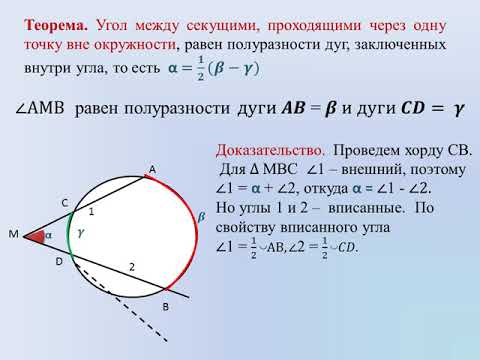 Центральный угол окружностиСкачать  Окружнось, дуга, длина дуги, центральный угол.Скачать  Задания ОГЭ по математике: решение варианта 17. Нахождение угла, образованного двумя радиусами..Скачать  Длина окружности. Площадь круга. 6 класс.Скачать  Углы в окружности | ФормулыСкачать  1 2 4 сопряжение окружностейСкачать  Окружность и круг, 6 классСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Длина окружности. Математика 6 класс.Скачать  Угол между хордой и касательной. 9 класс.Скачать  Задача на определение градусной мерыСкачать  |






































