Отрезки в прямоугольном треугольнике (4 видео)

Узнать ещё

Знание — сила. Познавательная информация

Содержание

Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике
Ход урока
I. ОРГМОМЕНТ
II. АКТУАЛИЗАЦИЯ ЗНАНИЙ
III. ИЗУЧЕНИЕ СВОЙСТВА ВЫСОТЫ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА, ПРОВЕДЕННОЙ ИЗ ВЕРШИНЫ ПРЯМОГО УГЛА
IV. ВВЕДЕНИЕ ПОНЯТИЯ СРЕДНЕГО ПРОПОРЦИОНАЛЬНОГО ДВУХ ОТРЕЗКОВ
V. УСВОЕНИЕ ПОНЯТИЯ СРЕДНЕГО ПРОПОРЦИОНАЛЬНОГО ДВУХ ОТРЕЗКОВ
VI. ВЫВОД СЛЕДСТВИЙ
VII. РЕШЕНИЕ ЗАДАЧ
VIII. ПОДВЕДЕНИЕ ИТОГОВ
IX. ПОСТАНОВКА ДОМАШНЕГО ЗАДАНИЯ
🎬 Видео

Видео:8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Пропорциональные отрезки в прямоугольном треугольнике

Запомнить соотношения, связывающие пропорциональные отрезки в прямоугольном треугольнике, помогает цветовая ассоциация.

Высота прямоугольного треугольника, проведенная к гипотенузе, делит ее на отрезки, которые называются проекциями катетов на гипотенузу.

Свойства прямоугольного треугольника:

1. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.

2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

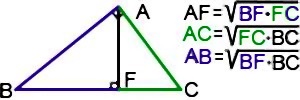
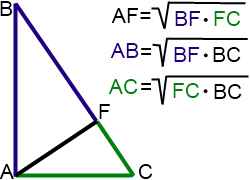
Например, в треугольнике ABC AF — высота, проведенная к гипотенузе BC, BF — проекция катета AB на гипотенузу, FC — проекция катета AC на гипотенузу.

Если выделить каждую пару — катет и его проекция на гипотенузу — одним цветом, запомнить пропорциональные отрезки в прямоугольном треугольнике можно быстро и легко.

Как бы ни был расположен на чертеже прямоугольный треугольник, цветовая ассоциация поможет найти пропорциональные отрезки и правильно составить связывающие их соотношения:

Выделить пропорциональные отрезки цветами можно на черновике. При решении задачи, в которой прямоугольный треугольник — только один из элементов чертежа, достаточно для нахождения связи между пропорциональными отрезками на черновике изобразить отдельный фрагмент с этим треугольником.

Видео:Пропорциональные отрезки в прямоугольном треугольнике. Видеоурок 14. Геометрия 8 классСкачать

Пропорциональные отрезки в прямоугольном треугольнике

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим пропорциональные отрезки в прямоугольном треугольнике. Соотношения между элементами прямоугольных треугольников позволяют легко вычислять неизвестные элементы прямоугольного треугольника. Мы сформулируем и докажем три теоремы, связывающие элементы прямоугольного треугольника, а также решим задачу на их применение.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»

Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Пропорциональные отрезки в прямоугольном треугольнике

Разделы: Математика

Цели урока:

ввести понятие среднего пропорционального (среднего геометрического) двух отрезков;
рассмотреть задачу о пропорциональных отрезках в прямоугольном треугольнике: свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла;
формировать у учащихся навыки использования изученной темы в процессе решения задач.

Тип урока: урок изучения нового материала.

План:

Оргмомент.
Актуализация знаний.
Изучение свойства высоты прямоугольного треугольника, проведенной из вершины прямого угла:
– подготовительный этап;
– введение;
– усвоение.
Введение понятия среднего пропорционального двух отрезков.
Усвоение понятия среднего пропорционального двух отрезков.
Доказательство следствий:
– высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;
– катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
Решение задач.
Подведение итогов.
Постановка домашнего задания.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Ход урока

I. ОРГМОМЕНТ

– Здравствуйте ребята, присаживайтесь. Все готовы к уроку?

II. АКТУАЛИЗАЦИЯ ЗНАНИЙ

– С каким важным математическим понятием вы познакомились на предыдущих уроках? (с понятием подобия треугольников)

– Давайте вспомним, какие два треугольника называются подобными? (два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника)

– Чем мы пользуемся при доказательстве подобия двух треугольников? (признаки подобия треугольников)

– Сформулируйте эти признаки (формулируют три признака подобия треугольников)

III. ИЗУЧЕНИЕ СВОЙСТВА ВЫСОТЫ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА, ПРОВЕДЕННОЙ ИЗ ВЕРШИНЫ ПРЯМОГО УГЛА

а) подготовительный этап

– Ребята, посмотрите пожалуйста на первый слайд. (Приложение) Здесь изображены два прямоугольных треугольника – и . и – высоты и соответственно. .

Задание 1. а) Определите, подобны ли и .

– Что мы используем при доказательстве подобия треугольников? (признаки подобия треугольников)

– Какой признак подобия будем использовать и почему? (первый признак, т.к. в задаче ничего неизвестно о сторонах треугольников)

– Сколько пар равных углов нам нужно найти? Найдите эти пары. (Две пары: 1. ∟В= ∟В1 (прямые),2. ∟A= ∟A₁)

– Сделайте вывод.(по первому признаку подобия треугольников

)

Задание 1. б) Определите, подобны ли и .

– Какой признак подобия будем использовать и почему? (первый признак, т.к. в задаче ничего неизвестно о сторонах треугольников)

– Сколько пар равных углов нам нужно найти? Найдите эти пары (т.к. треугольники прямоугольные, то достаточно одной пары равных углов: ∟A= ∟A₁)

– Сделайте вывод. (по первому признаку подобия треугольников заключаем, что данные треугольники подобны).

В результате беседы слайд 1 выглядит так:

б) открытие теоремы

Задание 2.

– Определите, подобны ли и , и . В результате беседы выстраиваются ответы, которые отражены на слайде.

– На рисунке было указано, что . Использовали ли мы эту градусную меру при ответах на вопросы заданий? (Нет, не использовали)

– Ребята, сделайте вывод: на какие треугольники разделяет прямоугольный треугольник высота, проведенная из вершины прямого угла? (делают вывод)

– Возникает вопрос: а будут ли эти два прямоугольных треугольника, на которые высота разбивает прямоугольный треугольник, подобны между собой? Давайте попробуем найти пары равных углов.

В результате беседы выстраивается запись:

– А теперь давайте сделаем полный вывод.(ВЫВОД: высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному)

– Т.о. мы с вами сформулировали и доказали теорему о свойстве высоты прямоугольного треугольника.

Установим структуру теоремы и сделаем чертеж. Что в теореме дано и что нужно доказать? Учащиеся записывают в тетрадь:

– Докажем первый пункт теоремы для нового рисунка. Какой признак подобия будем использовать и почему? (Первый, т.к. в теореме ничего неизвестно о сторонах треугольников)

– Сколько пар равных углов нам нужно найти? Найдите эти пары. (В данном случае достаточно одной пары: ∟A-общий)

– Сделайте вывод. Треугольники подобны. В результате показывается образец оформления теоремы

– Второй и третий пункты распишите дома самостоятельно.

в) усвоение теоремы

– Итак, сформулируйте еще раз теорему (Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному)

– Сколько пар подобных треугольников в конструкции «в прямоугольном треугольнике проведена высота из вершины прямого угла» позволяет найти эта теорема? (Три пары)

Ученикам предлагается следующее задание:

IV. ВВЕДЕНИЕ ПОНЯТИЯ СРЕДНЕГО ПРОПОРЦИОНАЛЬНОГО ДВУХ ОТРЕЗКОВ

– А теперь мы изучим с вами новое понятие.

Определение. Отрезок XY называется средним пропорциональным (средним геометрическим) между отрезками AB и CD, если

(записывают в тетрадь).

V. УСВОЕНИЕ ПОНЯТИЯ СРЕДНЕГО ПРОПОРЦИОНАЛЬНОГО ДВУХ ОТРЕЗКОВ

– Теперь обратимся к следующему слайду.

Задание 1. Найдите длину среднего пропорционального отрезков MN и KP, если MN = 9 см, KP = 16 см.

– Что дано в задаче? (Два отрезка и их длины: MN = 9 см, KP = 16 см)

– Что нужно найти? (Длину среднего пропорционального этих отрезков)

– Какой формулой выражается среднее пропорциональное и как мы его найдем?

(Подставляем данные в формулу и находим длину ср.проп.)

Задание №2. Найдите длину отрезка AB, если среднее пропорциональное отрезков AB и СD равно 90 см и CD = 100 см

– Что дано в задаче? (длина отрезка CD = 100 см и среднее пропорциональное отрезков AB и СD равно 90 см)

– Что нужно найти в задаче? (Длину отрезка AB)

– Как будем решать задачу? (Запишем формулу среднего пропорционального отрезков AB и СD, выразим из нее длину AB и подставим данные задачи.)

VI. ВЫВОД СЛЕДСТВИЙ

– Молодцы, ребята. А теперь давайте вернемся к подобию треугольников, доказанному нами в теореме. Сформулируйте еще раз теорему. (Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному)

– Давайте вначале будем использовать подобие треугольников и . Что из этого следует? (По определению подобия стороны пропорциональны сходственным сторонам )

– Какое равенство получится при использовании основного свойства пропорции? ()

– Выразите СD и сделайте вывод (;.

Вывод: высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой)

– А теперь докажите самостоятельно, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.

Доказывают самостоятельно, потом проверяем на слайде

VII. РЕШЕНИЕ ЗАДАЧ

Л.С. Атанасян «Геометрия 7-9», № 571(б)

– Прочитайте задачу. Что в задаче дано? (Дан прямоугольный )

– Что в задаче нужно найти? (Найти )

– Чем будет являться по отношению к и ? (Это среднее пропорциональное по следствию из доказанной теоремы)

– Как найти ? ()

– Как теперь найти ? (найдем из по теореме Пифагора: )

– Как найдем ? ( найдем из по теореме Пифагора: )

– Запишите ответ. (Ответ: )

VIII. ПОДВЕДЕНИЕ ИТОГОВ

– Подведем итог урока. С каким свойством высоты прямоугольного треугольника, проведенной из вершины прямого угла, мы сегодня познакомились? (Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному)

– Какое новое математическое понятие изучили? (Понятие среднего пропорционального двух отрезков.)

Высота прямоугольного треугольника, проведенная из вершины прямого угла есть среднее пропорциональное м/у…(-… отрезками, на которые делится гипотенуза этой высотой)

Катет прямоугольного треугольника есть среднее пропорциональное между…(-…гипотенузой и отрезком гипотенузы, заключенным между этим катетом и высотой)

– Где мы применяем изученные утверждения? (При решении задач)