Отражение вектора относительно нормали

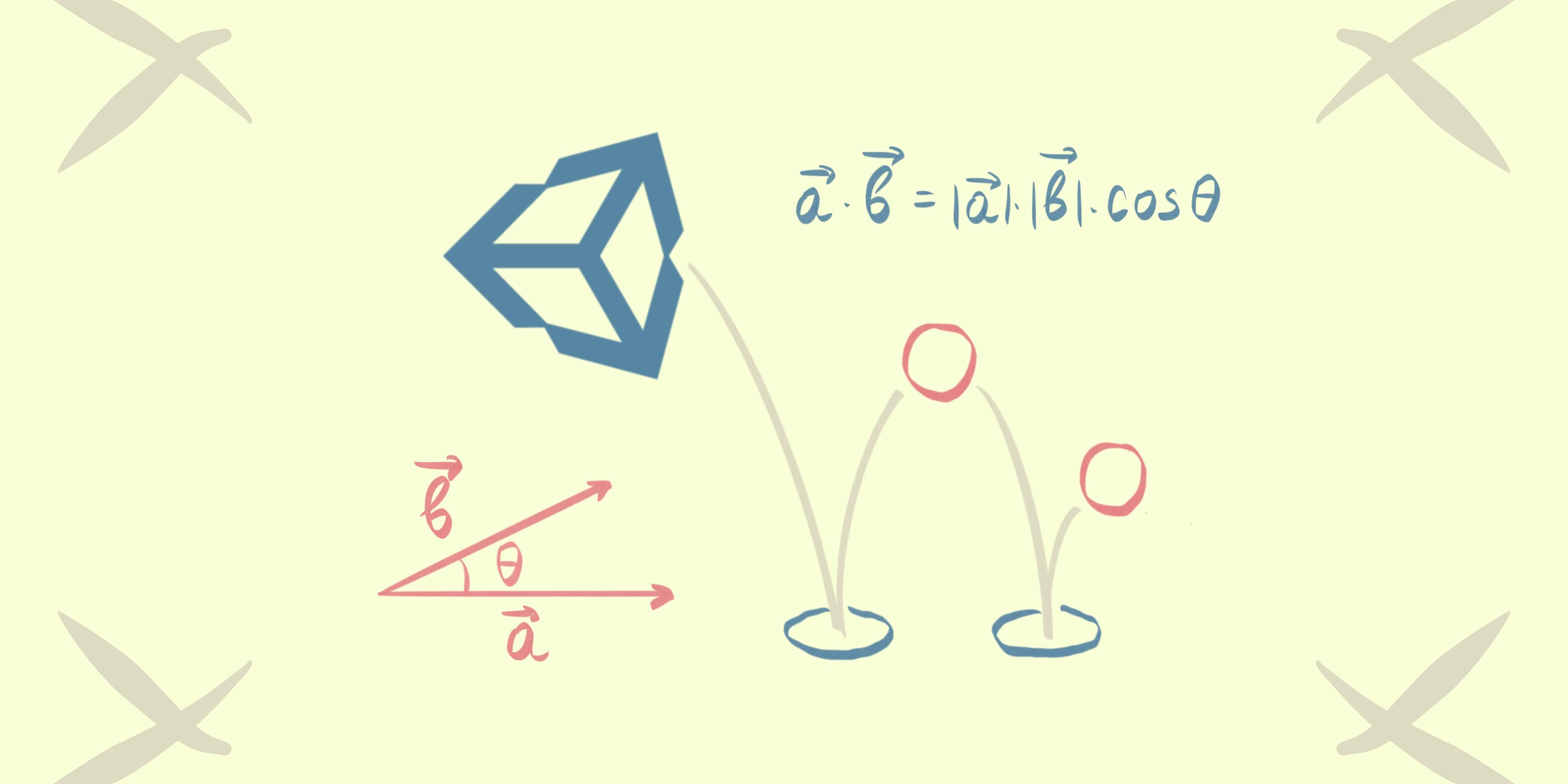
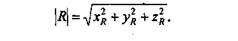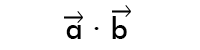Тема9. Построение реалистических изображений

В этом разделе мы рассмотрим методы, которые позволяют получить более-менее реалистичные изображения для объектов, моделируемых многогранниками и полигональными сетками.

Модели отражения света

Рассмотрим, как можно определить цвет пикселов изображения поверхности согласно интенсивности отраженного света при учете взаимного расположения поверхности, источника света и наблюдателя.

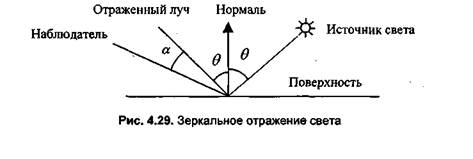
Зеркальное отражение света.Угол между нормалью и падающим лучом (Θ) равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости (рис. 4.29).

Поверхность считается идеально зеркальной, если на ней отсутствуют какие либо неровности, шероховатости. Собственный цвет у такой поверхности не наблюдается. Световая энергия падающего луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеивания не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0.5 мкм

Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны — чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.

При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов, близких к 90 градусам.

Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемые по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых, относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cosа) p , где а— угол отклонения от линии идеально отраженного луча. Показатель р находится в диапазоне от 1 до 200 и зависит от качества полировки. Запишем это таким образом:

где I— интенсивность излучения источника, K_s— коэффициент пропорциональности, который изменяется от 0 до 1.

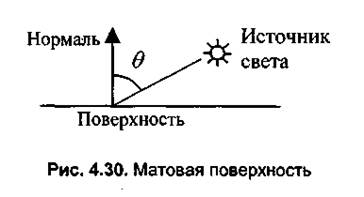
Диффузное отражение.Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения характерен, например, для гипса, песка бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности (рис. 4.30).

где I— интенсивность источника света, K_d— коэффициент, который учитывает свойства материала поверхности. Значение K_d находится в диапазоне от 0 до 1 . Интенсивность отраженного света не зависит от расположения наблюдателя.

Матовая поверхность имеет свой цвет. Наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета излучения источника света.

При создании реалистичных изображений следует учитывать то, что в природе, вероятно, не существует идеально зеркальных или полностью матовых поверхностей. При изображении объектов средствами компьютерной графики обычно моделируют сочетание зеркальности и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузной и зеркальной компонент:

где константы K_d, K_S определяют отражательные свойства материала.

Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов Θ и а. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:

где I_а — интенсивность рассеянного света, К_а — константа, изменяется от 0 до 1.

Можно еще усовершенствовать модель отражения, если учесть то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использование такого правила вызывает сложности, поэтому на практике часто реализуют модель, выражаемую эмпирической формулой:

где R — расстояние от центра проекции до поверхности, k — константа.

Как определить цвет закрашивания точек объектов в соответствии с данной моделью? Наиболее просто выполняется расчет в градациях серого цвет (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонент. Коэффициент! К_а и K_d различны для разных компонент — они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент K_s будет одинаковым для всех компонент цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонент.

Алгебра векторов

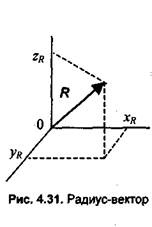
Здесь уместно сделать небольшое отступление от темы. Рассмотрим элементы алгебры векторов. Вектором называется отрезок прямой, соединяющий некоторые точки пространства А и В. Направление вектора — от начальной точки А к конечной точке В. Радиус-вектор R — это вектор, с начальной точкой в центре координат. Координатами радиус-вектора являются координаты конечной точки (рис. 4.31). Длина радиус-вектора часто называется модулем, обозначается как R|и вычисляется следующим образом:

Единичный вектор — это вектор, длина которого равна единице. Перечислим основные операции над векторами.

1. Умножение вектора на число X = Va. Результат — вектор X, длина которого в а раз больше вектора V. Если число а положительно, то направление вектора X совпадает с вектором V. При а

Видео:Направляющий и нормальный вектор прямой на плоскости | Векторная алгебраСкачать

Скалярное произведение в разработке игр: проекции и прыгающие мячики в Unity ⛹

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

furry.cat

Скалярное произведение – простой, но чрезвычайно полезный математический инструмент. Он кодирует отношение между величинами и направлениями двух векторов в единственное скалярное значение. Его можно использовать для вычисления проекции, отражения, расчета тени и постановки освещения. Из этого руководства вы узнаете:

• Геометрический смысл скалярного произведения.
• Как спроецировать один вектор на другой.
• Как измерить размер объекта вдоль произвольной оси.

• Как отразить вектор относительно плоскости.
• Как создать эффект отскока мяча от наклонной поверхности.

Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Скалярное произведение

Представьте два вектора a и b . Вектор характеризуется только направлением и величиной (длиной), поэтому не имеет значения, в каком месте плоскости он расположен. Допустим, оба вектора начинаются в одной точке:

a и b , выходящие из одной точки плоскости» data-src=»https://media.proglib.io/posts/2020/04/04/182e211c01704ab48d14f469d9838df4.png» > Два вектора a и b , выходящие из одной точки плоскости

Проекцию одного вектора на другой можно представить как отбрасывание тени от первого вектора в направлении, перпендикулярном второму:

Проекция одного вектора на другой

Как вы знаете, операция вычисления произведения векторов записывается так:

Далее в статье мы будем использоваться запись a * b .

Если между векторами острый угол, то длина проекции будет положительной величиной, если больше – то отрицательной.

Если b – единичный вектор, то величина проекции a на b – это просто произведение a * b .

Видео:Координаты вектора. 9 класс.Скачать

Вычисление скалярного произведения через косинус угла

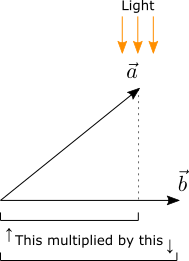
На схеме изображен прямоугольный треугольник. Угол между векторами a и b равен θ .

Два вектора образуют прямоугольный треугольник

Для начала требуется рассчитать величину проекции вектора a на вектор b – это нижний катет в нарисованном нами треугольнике. Длину катета стороны можно найти, умножив длину гипотенузы треугольника на косинус прилежащего угла.

a на вектор b – это катет прямоугольного треугольника» data-src=»https://media.proglib.io/posts/2020/04/04/c4a332573e7bdc88dcc72dddf457044d.png» > Проекция вектора a на вектор b – это катет прямоугольного треугольника

Итак, длина проекции равна произведению модуля вектора a на косинус угла θ . Скалярное произведение можно выразить следующим образом:

Формула вычисления скалярного произведения через косинус

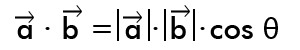
Эта формула лишний раз подтверждает, что порядок умножения не важен – в результат входят беззнаковые длины обоих векторов. Если оба вектора – единичные, правая часть формулы упрощается до cos(θ) . А если угол равен 90° (векторы перпендикулярны), то их произведение равно 0 .

Если угол острый (меньше 90°), результат будет положительным, так как косинус такого угла больше 0. Аналогично для тупого угла получится отрицательный результат. Таким образом, знак скалярного произведения дает нам некоторое представление о направлениях векторов.

Функция косинуса монотонно убывает на промежутке от 0 до 180° (от 1 до -1 ). Следовательно, чем ближе направления двух векторов, тем больше их скалярное произведение и наоборот.

• Направления совпадают, угол θ равен 0°, произведение равно |a| * |b| .
• Направления противоположны, угол θ равен 180°, произведение – -1* |a| * |b| .

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Вычисление скалярного произведения через компоненты векторов

Если наши векторы расположены в 3D-пространстве и имеют по три координаты каждый, не совсем понятно, где тот угол, косинус которого нужно вычислить. К счастью, существует другой способ расчета скалярного произведения – без всякой тригонометрии! Для начала нужно разложить каждый вектор на компоненты:

Разложение векторов на компоненты

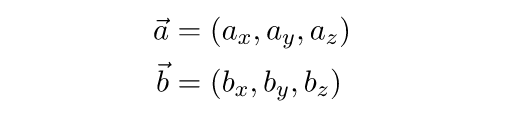
Намного проще и без всяких косинусов! В Unity есть встроенный метод Vector3.Dot для вычисления скалярного произведения двух векторов:

Его реализация выглядит следующим образом:

Нам известно, как найти длину вектора по его координатам:

Но ее можно выразить и через скалярное произведение вектора на себя:

Вернемся к формуле a * b = |a| * |b| * cos θ . При известных длинах векторов мы можем вычислить угол между ними с помощью функции арккосинуса:

Вычисление величины угла между векторами

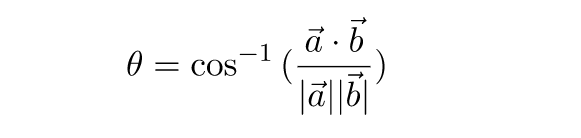
Если оба вектора являются единичными, мы можем упростить формулы:

Упрощенные формулы для единичных векторов

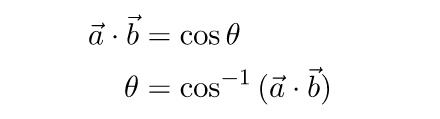
Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Проекция вектора

Теперь, когда нам известно геометрическое значение скалярного произведения векторов (произведение длины со знаком первого проецируемого вектора и длины второго вектора), мы можем перейти к практическому применению этого знания. Например, спроецируем один вектор на другой.

Пусть вектор с = project ba – это проекция вектора a на вектор b .

Вектор c – проекция вектора a на вектор b

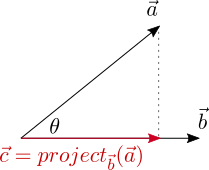
Возьмем единичный вектор в направлении вектора b . Он будет равен b / |b| . Если мы возьмем величину проекции a на b со знаком и умножим на этот единичный вектор, то получим вектор c . Cкалярное произведение a * b – это результат умножения длины b на длину проекции a на b . Отсюда получаем, что длину c со знаком можно найти, разделив скалярное произведение a * b на длину b :

Вычисление длины проекции одного вектора на другой

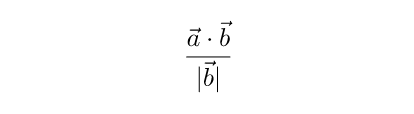
Умножив полученное значение на единичный вектор b / |b| , получаем формулу для нахождения проекции вектора:

Вычисление проекции одного вектора на другой

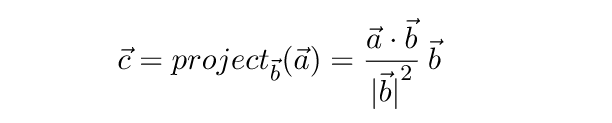
Вспомним теперь, что квадрат длины вектора равен его скалярному произведению на самого себя, и перепишем формулу:

Вычисление проекции одного вектора на другой

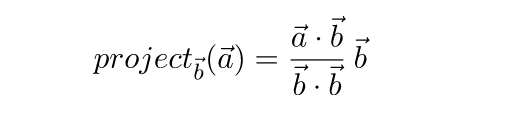
Если b – единичный вектор, то можно упростить еще больше:

Вычисление проекции вектора на единичный вектор

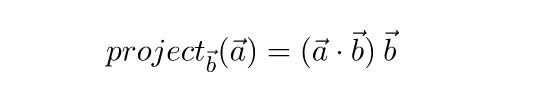
В Unity для вычисления проекции одного вектора на другой есть специальная функция Vector3.Project :

Вот так выглядит ее реализация:

Следует остерегаться возможного вырожденного случая, когда вектор, на который происходит проекция, – нулевой или имеет малую величину. При этом произойдет численный «взрыв» из-за деления на 0 или близкое к нему значение. Один из способов решить проблему – заранее вычислять величину вектора и при необходимости использовать резервный вариант (единичный вектор).

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Упраженение #1. Линейка

В качестве упражнения для закрепления знаний о векторной проекции сделаем линейку, которая измеряет размер объекта вдоль произвольной оси.

Линейка характеризуется базовой позицией (точка) и осью (единичный вектор):

Как спроецировать какую-либо точку ( Point ) на линейку? Прежде всего, найдем относительный вектор от базовой позиции линейки ( Base ) до этой точки. Затем спроецируем его на ось линейки ( Axis ). Проекция точки ( Projection ) – это базовое положение линейки, смещенное на проекцию относительного вектора.

Проекция точки на линейку

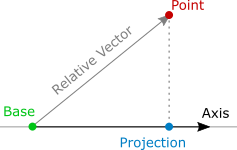
Промежуточное значение relativeDot в коде отражает, насколько далеко проекция точки находится от базового положения линейки – в направлении оси линейки, если она положительная, или в противоположном направлении, если отрицательная.

Чтобы найти размер объекта вдоль оси линейки, нужно провести такие измерения для каждой вершины меша (Mesh) и найти минимальное и максимальное значение. Ответ будет равен разнице между ними.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Отражение вектора

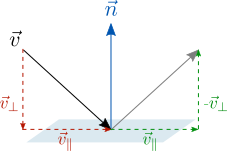
Еще одно практическое применение скалярного произведения – отражение вектора относительно плоскости. Рассмотрим вектор v и плоскость с нормальным вектором (перпендикуляром) n .

Отражение вектора v от плоскости

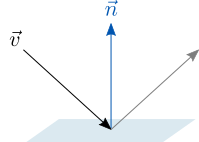
Мы можем разложить отражаемый вектор на параллельную и перпендикулярную к плоскости составляющие:

Разложение отражаемого вектора на составляющие

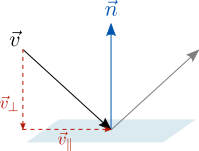
Сам вектор является суммой параллельной и перпендикулярной составляющих:

Разложение отражаемого вектора на составляющие

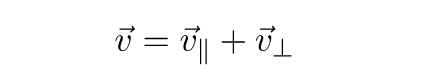
Перпендикулярный компонент, как вы уже догадались – это проекция вектор на нормаль плоскости. Параллельный компонент можно получить вычитанием этой проекции из самого вектора:

Получение параллельного плоскости компонента вектора

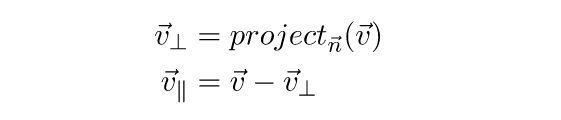
Теперь, чтобы получить искомый отраженный вектор, нужно перевернуть перпендикулярную составляющую и прибавить ее к параллельной:

Получение отраженного от плоскости вектора

Параллельный компонент можно заменить разностью самого вектора и перпендикулярной составляющей, тогда получим следующий вид формулы:

То есть разность самого вектора и его удвоенной проекции на нормаль плоскости.

В Unity, конечно же, есть встроенная функция для расчета отраженного вектора – Vector3.Reflect :

Так выглядит реализация согласно первой выведенной нами формуле:

Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Упражнение #2. Отскок мяча от наклонной плоскости

Теперь, когда мы знаем все об отражении вектора от плоскости, можно переходить на следующий уровень сложности. Попробуем сымитировать движение мяча, отскакивающего от склона.

Для моделирования траектории движения шара под действием силы тяжести мы будем использовать метод Эйлера.

Чтобы определить, когда мяч ударяется о склон, нужно как-то определить момент, когда мяч проникает в плоскость.

Сфера может быть определена центром ( C ) и радиусом ( R ). Плоскость определяется нормальным вектором ( n ) и точкой на плоскости ( P ). Вектор от P до С обозначим u .

Сфера и плоскость

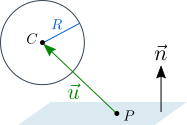
Если сфера НЕ проникает в плоскость, перпендикулярный плоскости компонент вектора u , должен иметь то же направление, что и вектор n , а также длину не менее R .

Перпендикулярный плоскости компонент вектора

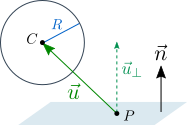
Другими словами, сфера не проникает в плоскость, если скалярное произведение векторов u и n больше R . В противном случае величина проникновения составляет R – u * n , и положение сферы нужно исправить.

Чтобы это сделать, можно просто переместить сферу в направлении нормали плоскости n на величину проникновения. Это лишь приближенное решение, которое не является физически правильным, но для упражнения оно хорошо подходит.

Добавим логику для коррекции позиции:

Нам также нужно отразить скорость, с которой движется сфера, относительно наклона, чтобы она правильно отскакивала.

Эта анимация демонстрирует идеальное отражение и выглядит неестественной. Мы ожидаем, что с каждым отскоком скорость мяча будет уменьшаться.

Это поведение обычно моделируется значением реституции (восстановления) между двумя сталкивающимися объектами. При 100% реституции мяч идеально отскакивает от плоскости. При 50% – величина перпендикулярной к плоскости составляющей скорости мяча будет уменьшена вдвое.

Величина реституции – это отношение величин перпендикулярного к плоскости компонента скорости мяча до и после отскока.

Вот пересмотренный с учетом коэффициента восстановления скорости вариант функции отражения:

Вот так выглядит обновленная функция SphereVsPlane :

Логика корректировки позиции заменяется логикой полноценного отскока:

Теперь мы можем устанавливать разные коэффициенты реституции для разных шариков:

Видео:Закон преломления света. Полное отражение | Физика 11 класс #28 | ИнфоурокСкачать

Заключение

Мы ответили на все вопросы, заданные в начале этого руководства.

• Скалярное произведение двух векторов – это произведение проекции первого вектора на второй (с учетом знака) и модуля второго вектора.
• Существует две формулы вычисления скалярного произведения: через косинус угла и через компоненты векторов.
• Скалярное произведение имеет множество полезных практических применений. Например, оно позволяет рассчитать проекцию вектора на другой вектор.
• С помощью скалярного произведения можно найти отраженный от плоскости вектор. На этой основе строятся различные физические модели, например, имитация отскока шарика от плоскости.

Расскажите в комментариях – разрабатываете ли вы сейчас какую-нибудь игру и если да, то о чем она. Каких уроков по Unity вам не хватает?

Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Вектор отражения

Определив нормаль к поверхности в анализируемой точке и зная положение источника света, можно вычислить направление идеально отраженного луча. Для идеального зеркала выполняется закон: угол падения равен углу отражения. Угол падения измеряется между нормалью и направлением на источник света, а угол отражения измеряется между нормалью и отраженным лучом (рис. 4.2).

Рис. 4.2. Отражение от идеального зеркала

В двумерном пространстве направление отраженного луча задается этим законом однозначно, а в трехмерном пространстве для вычисления направления соответствующего вектора нужно ввести дополнительное условие: в точке Р падающий и отраженный лучи, а также нормаль к поверхности должны лежать в одной плоскости, т. е. быть компланарными векторами. Это условие позволяет однозначно определить направление отраженного луча г по заданным векторам нормали п и падающего луча /. Поскольку нас интересует только направление отраженного луча г, то в дальнейшем будем предполагать, что все интересующие нас векторы являются ортами — векторами единичной длины.

Если 0, = 0_Г, то cosG/ = cos0_r. Используя скалярное произведение, получим соотношение, связывающее углы падения и отражения

Условие компланарности трех векторов означает, что г можно выразить линейной комбинацией / и п

Правую и левую часть уравнения умножим скалярно на п, получим

Второе соотношение, связывающее параметры а и |3, можно найти из условия, что вектор г должен быть единичным

Решая уравнение, получим, что г = 2(1п)п-.

Видео:Коллинеарность векторовСкачать

Вектор половинного направления

Для учета зеркального отражения света на основе модели Фонга скалярные произведения г ? v нужно вычислять для каждой точки поверхностей объектов сцены (рис. 4.3). Вектор v определяет направление наблюдателя. Можно упростить этот процесс, вычисляя промежуточный вектор единичной длиной h,

Угол между векторами п и И называется углом половинного направления (half-angle). Если вектор v лежит в той же плоскости, что и /, п и г, то выполняется соотношение 2г|> = ср.

Можно избавиться от вычисления вектора г, если заменить вычисление скалярного произведения г • v произведением п ? И.

Рис. 4.3. Определение вектора половинного направления Упражнения к главе 4

1. Найдите на поверхности сферы единичного радиуса четыре точки, находящиеся друг от друга на одинаковом расстоянии. Указание. Одну из точек можно выбрать произвольно; пусть это будет точка (0, 1, 0). В таком случае другие три лежат на плоскости у = —d, где d — некоторое положительное число.

• 2. Покажите, что если v лежит в той же плоскости, что и I, п и г, то угол половинного направления удовлетворяет условию 2гр = ф. Какое соотношение существует между этими углами в случае, если v не является компланарным остальным векторам?
• 3. Покажите, что вектор половинного направления h задает такую ориентацию поверхности, которая обеспечивает максимальное отражение светового потока к наблюдателю.
• 4. Найдите вектор преломленного луча, который определяет ориентацию поверхности, обеспечивающую максимальное отражение падающего луча в сторону наблюдателя.
• 5. Вычислите вектор отражения, если заданы вектор нормали и вектор падающего луча.

📹 Видео

Разложение вектора по базису. 9 класс.Скачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

A.7.23+ Симметрия и отражениеСкачать

Новое задание профиля №2. Все, что нужно знать о векторах | Аня МатеманяСкачать

Скалярное произведение векторов. 9 класс.Скачать

Длина вектора через координаты. 9 класс.Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать