Отношения между множествами всех выпуклых четырехугольников параллелограммов

Математика | 10 — 11 классы

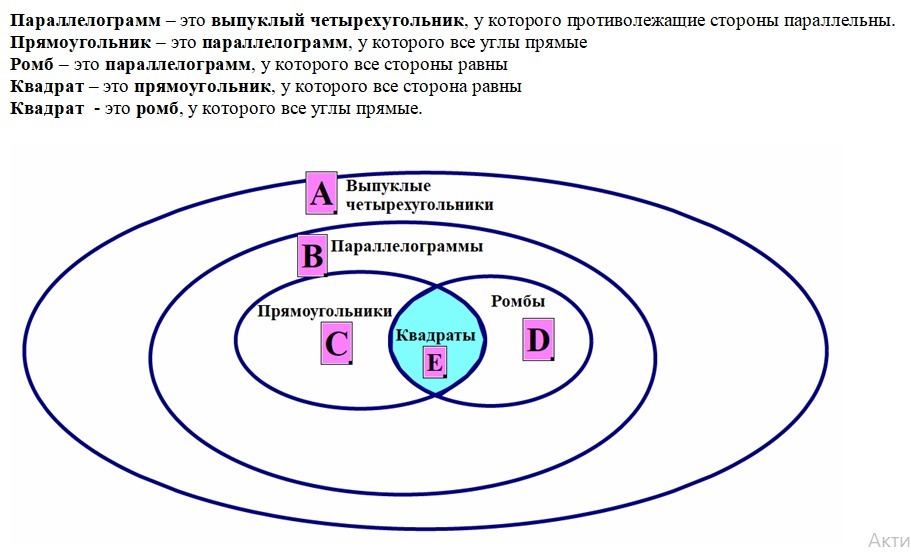
(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6.

Покажите каждое из множеств.

Параллелограмм – это выпуклый четырехугольник, у которого противолежащие стороны параллельны.

Прямоугольник – это параллелограмм, у которого все углы прямые

Ромб – это параллелограмм, у которого все стороны равны

Квадрат – это прямоугольник, у которого все сторона равны

Квадрат — это ромб, у которого все углы прямые.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ?

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ.

Какие из этих множеств являются подмножествами других множеств?

Видео:№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ?

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ!

Даны множества А, В, С.

Изобразите отношения между ними.

Укажите характеристическое свойство множеств АUВ, А∩С, А В, А ∩ (В С) : № 11.

А – множество учащихся в школе ;

В – множество девочек в школе ;

С – множество учащихся третьих классов в этой школе.

А – множество натуральных чисел ;

В – множество натуральных чисел, кратных 5 ;

С – множество натуральных чисел, кратных 4.

А – множество параллелограммов ;

В – множество четырехугольников ;

С – множество прямоугольников.

А – множество прямоугольников ;

В – множество четырехугольников ;

С – множество квадратов.

А – множество треугольников ;

В – множество прямоугольных треугольников ;

С – множество равнобедренных треугольников.

А – множество трапеций ;

В – множество параллелограммов ;

С – множество четырехугольников, имеющих прямой угол.

А – множество прямоугольных треугольников ;

В – множество равносторонних треугольников ;

С – множество равнобедренных треугольников.

А – множество натуральных чисел, кратных 5 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 4.

А – множество натуральных чисел, кратных 2 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 5.

А – множество параллелограммов ;

В – множество квадратов ;

С – множество ромбов.

Видео:Виды четырехугольников и свойства параллелограммовСкачать

Как может называться множество квадрат ромб круг?

Как может называться множество квадрат ромб круг?

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты?

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты!

Видео:Множества и операции над нимиСкачать

Решите систему неравенств?

Решите систему неравенств.

На каком из рисунков изображено множество ее решений?

Видео:Множество. Элементы множества. 5 класс.Скачать

Какой четырехугольник не имеет оси симметрии?

Какой четырехугольник не имеет оси симметрии?

A) ромб б) прямоугольник в) параллелограмм г) квадрат.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция?

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников?

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников.

Видео:§3. Отношения объектов и их множеств. 5 клСкачать

Запиши множество острых , множество прямых и множество тупых углов на рисунке ?

Запиши множество острых , множество прямых и множество тупых углов на рисунке .

Есть ли среди данных фигур прямоугольники .

Из букв входящих в каждой множество составь слова.

Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

Запиши множества острых, множество прямых и множество тупых углов на рисунке?

Запиши множества острых, множество прямых и множество тупых углов на рисунке.

Есть ли среди данных фигур прямоугольники?

На этой странице находится ответ на вопрос (Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?, из категории Математика, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Один угол х, второй х + 40 их сумма равно 90 уравнение : х + х + 40 = 90 2х = 90 — 40 2х = 50 х = 25 первый угол 25 второй угол 25 + 40 = 65.

В перовм ответ : 1700 А во втором незнаю.

901 + 799 — 92000 : 460 = 1700 — 200 = 1500 1541 + 759 — 76000 : 456 = 2300 — 166 = 2134.

8 в 3 степени 6 в 4 степени 7 в 5 степени x в 9 степени 15 в 3 степени 43 в 4 степени 8 в 8 степени ab в 7 степени дальше хз.

Просто начерти первый отрезок(например 5 или 7 см), а второй на 2 см больше, это ж просто. Если 5 то прибавь 2.

14М 60см = 1460см 1. 1460 * 3 = 4380см второй кусок 2. 4380 — 1460 = 2920 разница 3. 1460 + 4380 = 8540.

14м60см = 1460см 1. 1460умножить на 3 = 4380 2. 4380 + 1460 = 5840см = 58м40см 3. 4380 — 1460 = 2920см = 29метров20см.

L = 2 * пи * r. R = L / 2 * пи. R = 25, 12 / 2 * 3, 14 = 4(см). Ответ : r = 4 см.

Решение смотри на фотографии.

1) Если волчок покажет 7 или 8, то на кубике может выпасть любое число — оно все равно не совпадет. Это 6 + 6 = 12 вариантов. 2) Если на волчке выпадет любое число от 1 до 6, то нам подходит любое число на кубике, кроме такого же. Это 5 вариантов ..

Видео:Математика. 5 класс. Отношения между множествами /10.03.2021/Скачать

Лекция 2. Отношение между множествами.

Видео:Отношения объектов и их множеств | Информатика 6 класс #4 | ИнфоурокСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Лекция 2. Отношения между множествами.

Между двумя множествами существует пять видов отношений.

Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В = ∅ . Например, А = < a , c , k >, В = < d , e , m , n >, общих элементов у этих множеств нет, поэтому множества не пересекаются.

Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠ ∅ . Например, множества А = < a , c , k > и В = < c , k , m , n > пересекаются, т. к. у них есть общие элементы c , k .

Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В ⊂ А)

Пустое множество и само множество называют несобственными подмножествами . Остальные подмножества множества А называются собственными. Для каждого множества, состоящего из n элементов можно образовать 2 n подмножеств. Если рассматривают лишь подмножества некоторого множества U, то U называют универсальным множеством.

Если множества А и В состоят из одних и тех же элементов, то они называются равными.

Например, А = < a , c , k , m , n > и В = < m , n , a , c , k >, А = В.

Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.

Разбиение множества на классы называют классификацией.

Классификацию можно выполнять при помощи свойств элементов множества. Если выбирается только одно свойство, то такую классификацию называют дихотомической . Например, натуральные числа можно разбить на четные и нечетные. Буквы русского языка можно разбить на гласные и не гласные. Вообще, если на множестве Х задано одно свойство А, то это множество разбивается на два класса: первый класс – объекты, обладающие свойством А, второй класс – объекты, не обладающие свойством А.

Если элементы множества обладают двумя независимыми свойствами, то все множество разбивается на 4 класса. Например, на множестве натуральных чисел заданы два свойства: «быть кратным 2» и «быть кратным 3». При помощи этих свойств в множестве N можно выделить два подмножества А и В. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 6). Тогда в первый класс войдут числа, кратные 2 и 3, во второй – кратные 2, но не кратные 3, в третий – кратные 3, но не кратные 2, в четвертый – не кратные 2 и не кратные 3.

П р и м е р 1. Пусть Х – множество четырехугольников, А, В и С – его подмножества. Можно ли говорить о разбиении множества Х на классы А, В и С, если:

а) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, противоположные стороны которых не параллельны;

б) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, имеющих прямой угол?

Р е ш е н и е. а) Множества А, В и С попарно не пересекаются. Действительно, если у четырехугольника, противоположные стороны не параллельны, то он не может быть параллелограммом или трапецией. В параллелограмме противоположные стороны попарно параллельны, поэтому он не может принадлежать ни множеству В, ни множеству С. Наконец, в трапеции две противоположные стороны параллельны, а две другие не параллельны, поэтому трапеция не может принадлежать ни множеству А, ни множеству С. Объединение множеств А, В и С даст все множество четырехугольников. Условия классификации выполнены, множество всех четырехугольников можно разбить на параллелограммы, трапеции и четырехугольники, противоположные стороны которых не параллельны.

б) Множества А и В не пересекаются, но множества А и С имеют общие элементы, примером может служить прямоугольник, множества В и С тоже пересекаются: общим элементом является прямоугольная трапеция. Следовательно, нарушено первое условие классификации. Не выполняется и второе условие, так как некоторые четырехугольники не попадают ни в одно из подмножеств А, В или С, таким является четырехугольник с непараллельными сторонами и непрямыми углами. В этом случае множество Х на классы А, В и С не разбивается.

Задания для самостоятельной работы по теме:

Приведите примеры множеств А, В, С, если отношения между ними таковы:

2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?

3 . Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические свойства этих множеств.

5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.

6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø

7. Пусть Х= < x N/ 1 x 15>. Задайте с помощью перечисления следующие его подмножества:

А – подмножество всех четных чисел;

В – подмножество всех нечетных чисел;

С – подмножество всех чисел, кратных 3;

D – подмножество всех чисел, являющихся квадратами;

Видео:Математика. 4 класс. Отношения между множествами /06.10.2020/Скачать

Практическое занятие 1.2. Операции над множествами.

Семестр 1.

Практическое занятие 1.1. Множество. Способы задания множеств. Отношения между множествами.

Вопросы и задания для подготовки к занятию:

1. Приведите примеры множеств, включающих в себя однородные объекты. Например, мебель – это множество, которое включает в себя стул, стол, сервант и пр.

2. Запишите с помощью математических символов следующие предложения:

a. 4 натуральное число;

b. 2,1 не является целым числом;

c. множество В является подмножеством множества О;

d. множества К и С равны;

3. Задайте множества А и В другим способом, если А =, В = . Изобразите эти множества с помощью кругов Эйлера, каково отношение между этими множествами?

4. Сформулируйте определения понятий «характеристическое свойство множества», «равные множества», «подмножество».

5. Р – множество натуральных чисел, больших 7 и меньших 14. Выясните, какие из чисел 13, 10, 5, 7, 14 ему принадлежат, а какие не принадлежат. Запишите решение, используя математические символы.

6. А – множество решений уравнения . Верно ли, что А – пустое множество? Приведите примеры уравнений, множество решений которых состоит из:

a. одного элемента;

b. двух элементов;

c. трех элементов.

7. Запишите множество букв в слове «математика» и множество цифр в записи числа 515353.

8. Изобразите на координатной прямой множество Х, если:

a.

b.

c. .

9. Задайте двумя способами множество точек координатной прямой (рис. 1)

Задания для самостоятельной работы

1. Запишите множество А, элементами которого являются натуральные числа, меньшие 8, используя символические записи характеристического свойства и перечисления элементов множества. Верно, ли, что: а) 5 А; б) 0 А; в) 8 А?

2. Постройте прямую и отметьте на ней начало отсчета, единичный отрезок, точку А(5) и все точки, расстояние от которых от точки А: равно 2, не более 2.

3. Дано множество С = . Составьте подмножества множества С, состоящие из чисел, которые:

b. не делятся на 4;

c. не делятся на 5.

4. А – множество натуральных чисел, меньших 20; В, С, Е, Н – подмножества множества А, такие, что В состоит из чисел, кратных 6, С – из чисел, кратных 2, Е – из чисел, кратных 3, Н – из чисел, кратных 2 и 3 одновременно. Перечислите элементы множеств А, В, С, Е, Н и укажите среди них равные множества.

5. Отношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на рисунке. Покажите каждое из множеств.

6. Пусть разные строчные буквы обозначают разные предметы. Для каких из следующих пар множеств имеет место отношение А Ì В или В Ì А:

7. Какие из следующих пар множеств связаны между собой отношением включения:

d. А — множество многоугольников с периметром 4, В — множество квадратов с площадью 1?

8. Равны ли следующие множества: А = и В = ; А = и В =; А = <> и В = ;

Практическое занятие 1.2. Операции над множествами.

Вопросы и задания для подготовки к занятию:

1. Дайте определения понятиям «объединение множеств», «пересечение множеств». Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.

2. Сформулируйте свойства операций объединение и пересечение множеств. Проиллюстрируйте их с помощью кругов Эйлера.

3. Дайте определения понятиям «разность множеств», «дополнение множества». Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.

4. Сформулируйте свойства разности множеств.

5. Известно, что . Следует ли из этого, что:

°

°

°

6. Найдите пересечение, объединение, разность

° А= ;

° ;

° и ;

° ; Ø..

7. Известно, что . Следует ли из этого, что:

°

°

8. Найдите разность числового отрезка [1; 5] и числового отрезка [3; 7].

9. Сформулируйте условия, при которых истинны следующие высказывания:

° ;

° .

Задания для самостоятельной работы

1. Перечислите элементы, принадлежащие пересечению множества букв в слове «математика» и множества букв в слове «грамматика». Из каких элементов состоит объединение данных множеств?

2. Р – множество натуральных делителей числа 18, Н – множество натуральны делителей числа 24. укажите характеристическое свойство элементов пересечения множеств Р и Н и перечислите его элементы.

3. Найдите пересечение и объединение множеств К и М, если К – множество двузначных чисел, М – множество нечетных чисел. Верно ли, что: а) 21 ; б) ; в) ; г) .

4. Найти объединение и пересечение множеств А и В, если и .

5. Три множества Р, Н, М изображены тремя прямоугольниками (рис. 1). Отметьте штриховкой области, изображающие множество Х: а) М Н; б) Р Н; в) (Р Н) (Н М).

6. В – множество правильных многоугольников, Т – множество прямоугольников. Из каких фигур состоит объединение и пересечение множеств В и Т. Нарисуйте по две фигуры из каждого множества.

7. Даны множества: А =, В =, С = . Перечислите элементы множеств К=(АÈВ)ÇС и Р =А È ВÇ С. Содержится ли элемент m в множестве К, а элемент f в множестве Р?

8. А – множество чисел, кратных 2, В – множество чисел, кратных 3, С – множество чисел, кратных 5. Укажите характеристическое свойство элементов множества (А В) С и (А В) С.

9. Найдите объединение и пересечение множеств и дайте графическую иллюстрацию при помощи диаграмм Эйлера — Венна, если:

10. Изобразите на числовой прямой и запишите при помощи неравенства объединение и пересечение множеств Р и Q:

а) Р = , Q= ;

б) Р = , Q = ;

в) Р = , Q =

11. Множество А состоит из натуральных чисел от 2 до 10, множество В – из натуральных чисел от 5 до20. Перечислите элементы множеств А В и В А.

12. Р – множество двузначных чисел, М – множество четных натуральных чисел. изобразите данные множества при помощи кругов Эйлера, отметьте штриховкой разность множеств Р и М и укажите характеристическое свойство элементов, принадлежащей этой разности. Верно ли, что Р М содержит числа 21; 17?

13. Дано множество . Запишите два подмножества множества Х и дополнение этих подмножеств до множества Х.

14. Сформулируйте характеристическое свойство элементов дополнения множества Р до множества треугольников, если: а) Р – множество остроугольных треугольников; б) Р – множество равносторонних треугольников.

15. Найдите дополнение множества У до множества Х, если:

a) Х – множество точек прямой АВ;

b) множество точек отрезка АВ;

c) Х – множество точек квадрата, У – множество точек круга, вписанного в этот квадрат.

16. Найдите дополнение:

d) множества четных натуральных чисел до множества N;

e) множества отрицательных чисел до множества Z;

f) множества целых чисел до множества Q.

2. Отметьте на координатной прямой множество А и укажите характеристическое свойство элементов его дополнения до множества R, если: а) ; б) ; в) .

3. Множества А, В и С таковы, что Ø. Изобразите их при помощи кругов Эйлера и отметьте штриховкой области, представляющие множества (А В) С, А В С, А (В С), А В С. Для каждого случая сделайте отдельный чертеж.

4. А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. постройте круги Эйлера для данных множеств и отметьте штриховкой области, изображающие множества: а) А В С; б) В С; в) (А В)’ С.

5. Постройте три круга, изображающие три попарно пересекающихся множества А, В и С, и выделите штриховкой области, представляющие множества:

💥 Видео

Четырехугольники. Вебинар | МатематикаСкачать

Пересечение множеств. Объединение множеств. 5 класс.Скачать

Математика. 4 класс. Закрепление. Отношения между множествами /08.10.2020/Скачать

Проверяем свойства отношенийСкачать

Практикум. Логические отношения между понятиями.Скачать

Математика. Отношения между множествами. 4 класс. Урок 25Скачать