Основание прямой призмы трапеция параллельные стороны которой

основание прямой призмы трапецияу которой параллельные стороны равны 9 и 19 см. три боковые грани призмы квадраты со стороной 9 см. опредилить полную поверхность

полная поверхность равна: 4боковые плоскости плюс 2 основания
3 стороны трапеции = 9, ещё одна сторона равна 19, а высота равна 9.
значит площадь основания будет равна: 1/2*(9+19)*(корень из 56)=28 корней из 14
А полная площадь будет равна: 2*(28корней из 14)+81+81+81+171=414+(56 корней из 14)

Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

В сновании прямой призмы трапеция у которой параллельные стороны 9 и 39 см?

Геометрия | 10 — 11 классы

В сновании прямой призмы трапеция у которой параллельные стороны 9 и 39 см.

3 боковые грани призмы квадраты.

Найдите объем призмы.

Одно основание — 9 другое — 39, проводим 2 высоты.

Они отсекают 2 прямоугольных треугольника по сторонам и оставляют в сетедине прямоугольник.

Сторона более короткого основания равна противоположной — 9.

Тогда получим что основания тех самых отсеченных треугольников равны (39 — 9) / 2 = 15.

Теперь рассмотрим один из них.

Катет равен 15 — гипотенуза не может быть больше катета, след.

К. 3 боковые грани — квадраты).

По теореме пифагора находим 3ю сторону(высоту трапеции) — она равна корню из 39 ^ 2 — 15 ^ 2 равна 36.

Площадь трапеции(основания призмы) равна полусумме оснований умноженная на высоту : (39 + 9) / 2 * 36 = 864.

3 из боковых граней — квадраты(а мы уже поняли что квадратами являются те чьи стороны равны 39), то и высота призмы равна 39.

Получим что объем призмы равен основанию умноженному на высоту : 864 * 39 = 33696(см ^ 3).

Видео:№222. Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 смСкачать

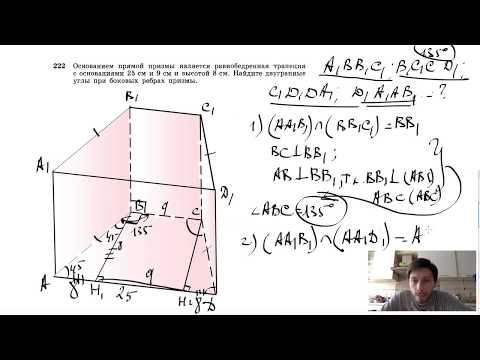
Основание прямой призмы — трапеция с основаниями 10 см?

Основание прямой призмы — трапеция с основаниями 10 см.

Найти полную поверхность призмы, если три ее боковые грани — квадраты со стороной 10 см.

Видео:№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Основание прямой призмы — прямоугольный треугольник с катетами 3 и 4 см, большая боковая грань — квадрат?

Основание прямой призмы — прямоугольный треугольник с катетами 3 и 4 см, большая боковая грань — квадрат.

Найти объем призмы.

Видео:🔴 В прямоугольной трапеции основания ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Основание прямой призмы – равнобочная трапеция, одно из оснований которой в два раза больше другого?

Основание прямой призмы – равнобочная трапеция, одно из оснований которой в два раза больше другого.

Непараллельные боковые грани призмы – квадраты.

Высота призмы равна 6 см.

Площадь боковой поверхности призмы равна 144 см .

Вычислите объем призмы.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Основание прямой призмы — прямоугольный треугольник с катетами 6 и 8?

Основание прямой призмы — прямоугольный треугольник с катетами 6 и 8.

Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань — квадрат.

Видео:Геометрия 8 класс (Урок№4 - Трапеция)Скачать

Основанием прямой призмы является равнобедренная трапеция с основаниями, равными 9 см и 21 см, и диагональю 17 см?

Основанием прямой призмы является равнобедренная трапеция с основаниями, равными 9 см и 21 см, и диагональю 17 см.

Две боковые грани призмы — квадраты.

Найдите объем призмы.

Видео:🔴 В основании прямой призмы лежит прямоугольный ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Боковые грани правильной треугольной призмы являются квадратами?

Боковые грани правильной треугольной призмы являются квадратами.

Найдите угол между непересекающимися диагоналями боковых сторон призмы.

Видео:🔴 В основании прямой призмы лежит ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Основание прямой призмы — равнобедренный треугольник, две стороны которого равны 13 см?

Основание прямой призмы — равнобедренный треугольник, две стороны которого равны 13 см.

Одна из боковых граней призмы — квадрат, площадь которго равна 100 квадратных см.

Найдите объем призмы.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Основание прямой призмы равнобедренный треугольник с боковой стороной 5дм и периметром 18дм?

Основание прямой призмы равнобедренный треугольник с боковой стороной 5дм и периметром 18дм.

Найдите обьем призмы, если одна ее боковая грань квадрат.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Основание прямой призмы — равнобедренный треугольник, две стороны которого равны 13 см?

Основание прямой призмы — равнобедренный треугольник, две стороны которого равны 13 см.

Одна из боковых граней призмы — квадрат, площадь которого равна 100 квадратных см.

Найдите объём призмы.

Видео:11 класс, 31 урок, Объем прямой призмыСкачать

Все боковые грани призмы, основание которой правильный шестиугольник со стороной 2 корня из 5, квадраты?

Все боковые грани призмы, основание которой правильный шестиугольник со стороной 2 корня из 5, квадраты.

Найдите большую диагональ призмы.

На странице вопроса В сновании прямой призмы трапеция у которой параллельные стороны 9 и 39 см? из категории Геометрия вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Видео:8 класс, 6 урок, ТрапецияСкачать

Особенности трапециевидной призмы и способ расчета объема

трапециевидная призма это призма такая, что задействованные полигоны являются трапециевидными. Определение призмы — это такое геометрическое тело, которое образовано двумя равными и параллельными друг другу многоугольниками, а остальные их грани являются параллелограммами..

Призма может иметь разные формы, которые зависят не только от количества сторон многоугольника, но и от самого многоугольника..

Если многоугольники, входящие в состав призмы, являются квадратами, то это отличается от призмы, которая включает в себя, например, бриллианты, даже если оба многоугольника имеют одинаковое количество сторон. Таким образом, это зависит от того, какой четырехугольник участвует.

Видео:№235. Основанием прямой призмы является прямоугольный треугольник с острым углом φ. ЧерезСкачать

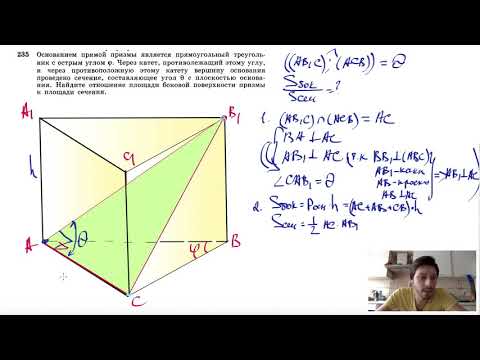
Характеристики трапециевидной призмы

Чтобы увидеть характеристики трапециевидной призмы, вы должны сначала узнать, как она нарисована, затем, каким свойствам соответствует основание, какова площадь поверхности и, наконец, как рассчитывается ее объем..

1- Рисование трапециевидной призмы

Чтобы нарисовать его, нужно сначала определить, что такое трапеция.

Трапеция представляет собой неправильный многоугольник с четырьмя сторонами (четырехугольник), так что у него есть только две параллельные стороны, называемые основаниями, а расстояние между его основаниями называется высотой.

Чтобы нарисовать прямую трапециевидную призму, начните с рисования трапеции. Затем вертикальная линия длиной «h» проецируется из каждой вершины и, наконец, рисуется другая трапеция, так что ее вершины совпадают с концами ранее нарисованных линий..

Вы также можете иметь наклонную трапециевидную призму, конструкция которой аналогична предыдущей, вам просто нужно нарисовать четыре линии, параллельные друг другу..

2- Свойства трапеции

Как было сказано ранее, форма призмы зависит от многоугольника. В частном случае трапеции мы можем найти три различных типа основ:

-Трапециевидный прямоугольник: является ли эта трапеция такой, что одна из ее сторон перпендикулярна ее параллельным сторонам или что она просто имеет прямой угол.

-Равнобедренная трапеция: трапеция такая, что ее непараллельные стороны имеют одинаковую длину.

Шкала трапеции: это та трапеция, которая не равнобедренная или прямоугольная; его четыре стороны имеют разную длину.

Как вы можете видеть в соответствии с типом трапеции, будет получена другая призма.

3- Площадь поверхности

Чтобы вычислить площадь поверхности трапециевидной призмы, нам нужно знать площадь трапеции и площадь каждого параллелограмма..

Как вы можете видеть на предыдущем изображении, область включает в себя две трапеции и четыре разных параллелограмма..

Площадь трапеции определяется как T = (b1 + b2) xa / 2, а площади параллелограммов: P1 = hxb1, P2 = hxb2, P3 = hxd1 и P4 = hxd2, где «b1» и «b2» основания трапеции, «d1» и «d2» непараллельные стороны, «a» — высота трапеции, а «h» — высота призмы..

Следовательно, площадь поверхности трапециевидной призмы A = 2T + P1 + P2 + P3 + P4.

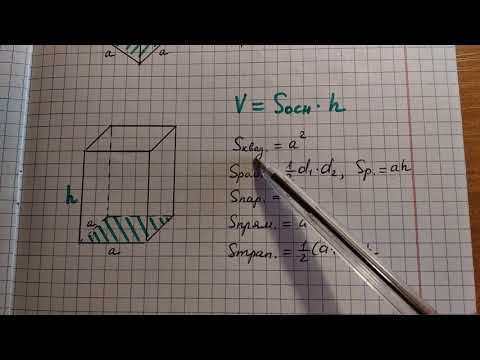
4- Том

Поскольку объем призмы определяется как V = (площадь многоугольника) x (высота), можно сделать вывод, что объем трапециевидной призмы равен V = Txh..

5- Приложения

Одним из наиболее распространенных объектов, имеющих форму трапециевидной призмы, является золотой слиток или пандусы, используемые в гонках на мотоциклах..

🔍 Видео

Геометрия Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CDСкачать

КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

№231. Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 60°. МеньшаяСкачать

Объем прямой призмы.Скачать

Строим проекции равнобедренной трапеции и определяем углы наклона ее высоты и плоскости к П1 и П2Скачать

Трапеция. Свойства. Задачи. Найти углы трапеции. ПериметрСкачать