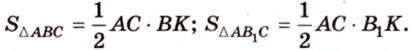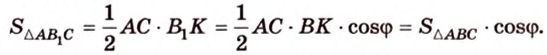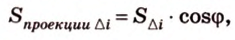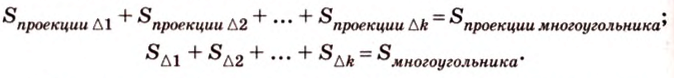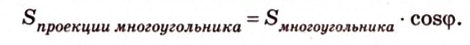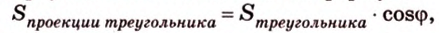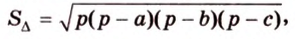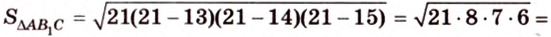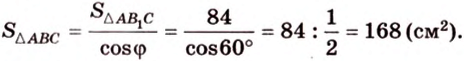Ортогональная проекция равнобедренного треугольника

Геометрия | 10 — 11 классы

Ортогональная проекция равнобедренного треугольника есть равносторонний треугольник со стороной 6см, одна сторона которого является основанием данного равнобедренного треугольника.

Найдите площадь равнобедренного треугольника, если его плоскость образует с плоскостью проектирования угол, равный 45 градусов.

Проекция равнобедренного треугольника есть равносторонний треугольник со стороной b = 6см,

площадь равностороннего треугольника S = 1 / 2 b ^ 2 sin60 = 1 / 2 6 ^ 2√3 / 2 = 9√3 см2

если плоскость равнобедренногообразует с плоскостью проектирования угол, равный 45 градусов, то площадь равнобедренного

Sp = S / cos45 = 9√3 / (1 / √2) = 9√6 см2

Видео:Построение равнобедренного треугольникаСкачать

Треугольник АВС, площадь котрого равна 24 см , является ортогональной проекцией равностороннего треугольника А1В1С1 со сторой 8 см?

Треугольник АВС, площадь котрого равна 24 см , является ортогональной проекцией равностороннего треугольника А1В1С1 со сторой 8 см.

Найдите угол между плоскостями АВС и А1В1С1.

Видео:ПОСТРОИТЬ ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА ПО ЗАДАННЫМ УСЛОВИЯМ. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.Скачать

1) точки к плоскости проведены две наклонные, угол между которыми 60, а угол между их проекциями 90?

1) точки к плоскости проведены две наклонные, угол между которыми 60, а угол между их проекциями 90.

Длины проекций наклонных на плоскость равны по 3 см каждая.

Вычислить расстояние от точки до плоскости 2) Основа равнобедренного треугольника совпадает со стороной правильного треугольника.

Основой перпендикуляра, проведенного с вершины первого треугольника в плоскости второго, является вершина правильного треугольника.

Боковая сторона равнобедренного треугольника равна 6 корень 5, а угол между плоскостями этих треугольников составляет 30 градусов.

Вычислить сторону правильного треугольник 3)Ортогональной проекцией трапеции является равносторонняя трапеция с основами 7 и 25 и диагоналями перпендикулярными к боковым сторонам.

Угол между плоскостями этих трапеций равна 60 градусов.

Вычислить площадь трапеции проектируемог.

Видео:ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЛЬНИКА НА П1/П2 и углы наклона его плоскости к плоскостям проекцийСкачать

В равнобедренном треугольнике основание 9 см, боковая сторона 8 см, угол при основании 30 градусов?

В равнобедренном треугольнике основание 9 см, боковая сторона 8 см, угол при основании 30 градусов.

Найдите площадь треугольника.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Если если основание и боковая сторона одного равнобедренного треугольника равна основанию и боковой стороне другого равнобедренного треугольника, то они равны?

Если если основание и боковая сторона одного равнобедренного треугольника равна основанию и боковой стороне другого равнобедренного треугольника, то они равны?

Видео:Построение треугольника в трёх проекцияхСкачать

ПЕРИМЕТР РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА РАВЕН 58 СМ?

ПЕРИМЕТР РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА РАВЕН 58 СМ.

ЕГО ОСНОВАНИЕ ЯВЛЯЕТСЯ ОДНОЙ ИЗ СТОРОН РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА ПЕРИМЕТР КОТОРОГО РАВЕН 42 СМ.

НАЙДИТЕ СТОРОНЫ РАВАНОБЕДРЕННОГО ТРЕУГОЛЬНИКА.

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

В равнобедренном треугольнике боковая сторона равна 8 см, а угол при основании равен 15 градусов?

В равнобедренном треугольнике боковая сторона равна 8 см, а угол при основании равен 15 градусов.

Найдите площадь этого треугольника.

Видео:Урок 17. Площадь ортогональной проекции Задание 14 ЕГЭ по математике. Стереометрия с нуля.Скачать

Периметр равностороннего треугольника равен 18 см одна из его сторон является основанием равнобедренного треугольника, периметр которого равен 20 см найдите стороны равнобедренного треугольника?

Периметр равностороннего треугольника равен 18 см одна из его сторон является основанием равнобедренного треугольника, периметр которого равен 20 см найдите стороны равнобедренного треугольника.

Видео:134 Равнобедренный прямоугольный треугольник, проекция которого подобна ему, но меньшей площадиСкачать

В равнобедренном треугольнике боковая сторона 4 см а угол при основании 75 градусов найдите площадь треугольника?

В равнобедренном треугольнике боковая сторона 4 см а угол при основании 75 градусов найдите площадь треугольника.

Видео:Ортогональная проекция и ортогональная составляющая. ТемаСкачать

Основание равнобедренного треугольника 8 см, а угол между боковыми сторонами 60 градусов?

Основание равнобедренного треугольника 8 см, а угол между боковыми сторонами 60 градусов.

Найдите площадь треугольника.

Видео:Площадь ортогональной проекции многоугольникаСкачать

Основание равнобедренного треугольника 8 см, а угол между боковыми сторонами 60 градусов?

Основание равнобедренного треугольника 8 см, а угол между боковыми сторонами 60 градусов.

Найдите площадь треугольника.

Вы находитесь на странице вопроса Ортогональная проекция равнобедренного треугольника есть равносторонний треугольник со стороной 6см, одна сторона которого является основанием данного равнобедренного треугольника? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Видео:Площадь ортогональной проекцииСкачать

Ортогональное проецирование — определение и вычисление с примерами решения

Ортогональное проецирование:

Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.

Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой

Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.

Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.

Площадь ортогональной проекции

Теорема 5

Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.

Как пример многоугольника возьмем (рис. 6.41). Проекцией на плоскость является . Проведем высоту треугольника . По теореме
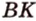
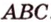
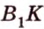
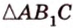
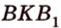
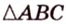
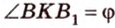
о трех перпендикулярах — высота . Угол — угол между плоскостью и плоскостью проекции. Пусть . Тогда

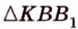
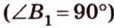
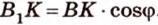
Учитывая, что прямоугольный , имеем:. Поэтому

Итак, . Теорема доказана.

Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство

где 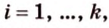поскольку угол между плоскостями этих треугольников и плоскостью их проекций будет один и тот же. Все эти равенства сложим почленно:

Получим в левой части равенства площадь проекции многоугольника, а в правой — площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда

Т.е. и для этого случая теорема истинна.

Пример:

Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.

Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:

где 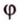— угол между плоскостью треугольника и плоскостью проекции.
По формуле Герона найдем площадь :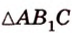

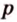
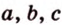
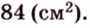
где — полупериметр треугольника, — его стороны.

Тогда

• Декартовы координаты на плоскости
• Декартовы координаты в пространстве
• Геометрические преобразования в геометрии
• Планиметрия — формулы, определение и вычисление
• Параллельность прямых и плоскостей
• Перпендикулярность прямой и плоскости
• Взаимное расположение прямых в пространстве, прямой и плоскости
• Перпендикулярность прямых и плоскостей в пространстве

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Построение проекции равнобедренного прямоугольного треугольника АВС (катет равен 200 мм), если АМ и АN направление катетов

Страницы работы

Содержание работы

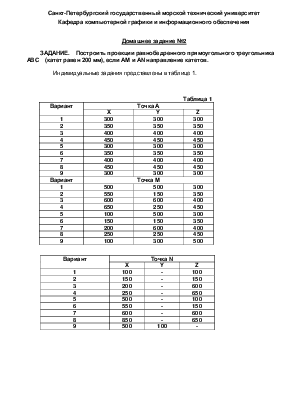
Санкт-Петербургский государственный морской технический университет

Кафедра компьютерной графики и информационного обеспечения

Домашнее задание №2

ЗАДАНИЕ. Построить проекции равнобедренного прямоугольного треугольника АВС (катет равен 200 мм), если АМ и АN направление катетов.

Индивидуальные задания представлены в таблице 1.

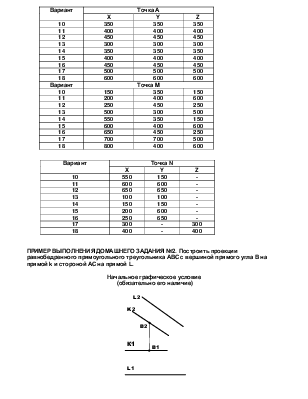
ПРИМЕР ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №2. Построить проекции равнобедренного прямоугольного треугольника АВС с вершиной прямого угла В на прямой k и стороной АС на прямой L.

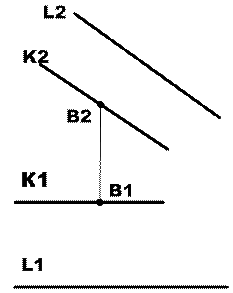
Начальное графическое условие

(обязательно его наличие)

Комментарий к решению задачи: для решения конструктивных задач полезно рисовать модель заданной фигуры в плане, для того, чтобы грамотно использовать ее геометрические характеристики. Одновременно надо внимательно проанализировать начальное условие. На рис.1 представлена модель в плане, а на рис.2 решение поставленной задачи.

Рис.1. Модель задачи в плане.

Из начального условия видно, что заданные прямые kиL параллельны фронтальной плоскости проекций и, следовательно, могут быть сделаны следующие важные выводы (см. рис.2):

— из заданной точки В2 можно проводить линию, перпендикулярную к фронтальным проекциям прямых k2 и L2 одновременно;

-т.к. гипотенуза заданного треугольника должна располагаться на прямой L, то ее фронтальная проекция А2С2 будет равна истинной величине гипотенузы АС.

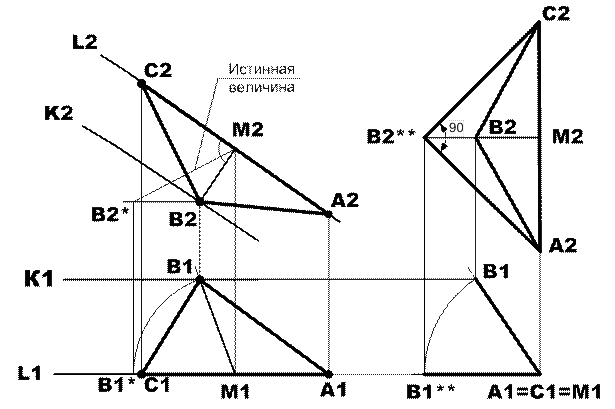
Сделанные выводы позволяют создать модель решения задачи (рис.1), в которой искомый треугольник построен следующим образом:

— из точки М проведена высота ВМ;

— известно, что высота, проведенная из вершины прямого угла, делит равнобедренный прямоугольный треугольник на два равных равнобедренных прямоугольных треугольника с вершиной прямого угла у основания высоты. Следовательно ВМ=МА, т.е. гипотенуза искомого треугольника в два раза больше его высоты;

— поскольку проекции высоты ВМ могут быть легко построены, то не составляет труда найти истинную величину гипотенузы АС и, следовательно, построить проекции треугольника АВС.

Рис.2. Построение проекций равнобедренного прямоугольного треугольника.

1) из точки В2 провести перпендикуляр к L2 и построить проекции высоты В2М2 и В1М1;

2) методом вращения, повернув высоту ВМ до положения параллельного фронтальной плоскости проекций, определить ее истинную величину-это проекция М2В2*;

3) отложить отрезок М2В2* на линии L2 в разные стороны от точки М2 для построения проекций вершин А2 и С2 искомого треугольника;

4) построить фронтальную А2В2С2 и горизонтальную А1В1С1 проекции искомого треугольника.

Проверка: построенные проекции треугольника искажены, поскольку заданный треугольник находится в общем положении в пространстве. Убедиться в правильности выполненных построений можно только определив истинную величину треугольника. Для этого методом вращения сначала треугольник переведен в проецирующее положение, которому соответствуют фронтальная проекция А2С2В2 при вертикальном расположении гипотенузы А2С2 и горизонтальная проекция в виде отрезка прямой А1С1В1. Далее проецирующий треугольник надо повернуть до положения параллельного плоскости П2, которому соответствуют горизонтальная проекция А1С1В1** и фронтальная проекция А2С2В2**. При этом проекция А2С2В2** равна по величине истинной. На рис.2 видно, что истинная величина является равнобедренным прямоугольным треугольником с вершиной прямого угла в точке В, что соответствует условию задачи.

💥 Видео

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Подготовка к ЕГЭ. Геометрия (Янтранова С.С.) - 8 лекцияСкачать

Проекции точки,отрезка,плоскости в ортогональном проецировании.Введение(Часть2.ПРОЕКЦИОННОЕЧЕРЧЕНИЕ)Скачать

Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

Площадь ортогональной проекции многоугольникаСкачать

Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

Строим проекции равнобедренной трапеции и определяем углы наклона ее высоты и плоскости к П1 и П2Скачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать