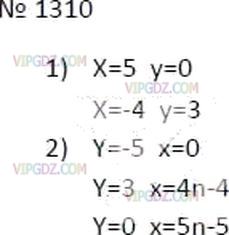Как найти ординату точки окружности абсцисса которой равна (3 видео)

Содержание

Решение на Упражнение 1310 из ГДЗ по Математике за 6 класс: Мерзляк А.Г.
Условие
Решение 1
Решение 2
Популярные решебники
Дано уравнение окружности x2+y2=169.
9 класс. Геометрия. Метод координат. Уравнение окружности.
9 класс. Геометрия. Метод координат. Уравнение окружности.
Вопросы
Поделись с друзьями
Комментарии преподавателя
Решение задач
Заключение
📸 Видео

Видео:Алгебра 7 класс. 28 сентября. Зная абсциссу найти ординатуСкачать

Решение на Упражнение 1310 из ГДЗ по Математике за 6 класс: Мерзляк А.Г.

Условие

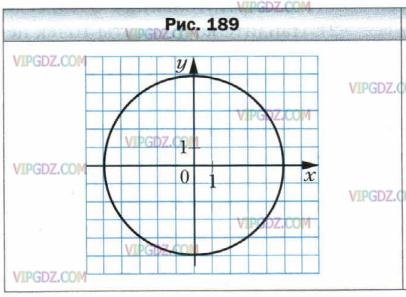
На координатной плоскости проведена окружность (рис.189).

1) Найдите ординату точки, принадлежащей этой линии, абсцисса которой равна: 5; −4.
2) Найдите абсциссу точки, принадлежащей этой линии, ордината которой равна: −5; 3; 0.

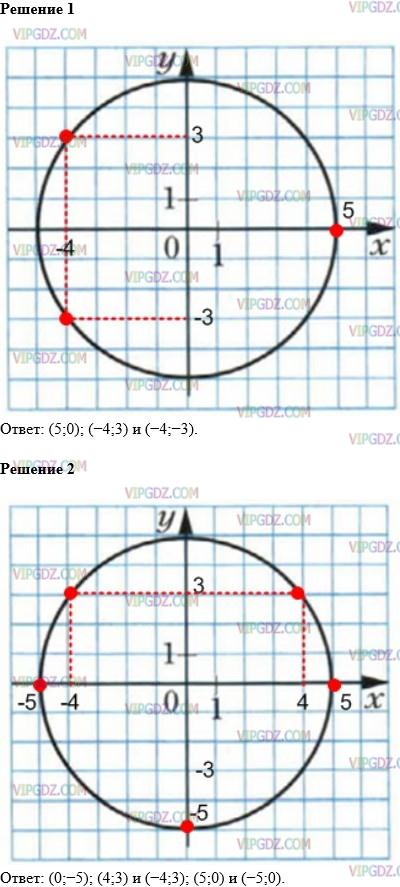
Решение 1

Решение 2

Поиск в решебнике

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Дано уравнение окружности x2+y2=169.

1. Найди ординату точек на этой окружности, абсцисса которых — 13.

(запиши обе координаты точек, в точке A ординату со знаком » — «, в точке B — со знаком » + «; если второй точки нет, вместо координат пиши координаты первой точки).

2. Найди абсциссу точек на этой окружности, ордината которых 13.

(запиши обе координаты точек, в точке C абсциссу со знаком » — «, в точке D — со знаком » + «; если второй точки нет, вместо координат пиши координаты первой точки).

Видео:10 класс, 11 урок, Числовая окружностьСкачать

9 класс. Геометрия. Метод координат. Уравнение окружности.

Оглавление
Занятия
Обсуждение
О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Дан график производной Найти абсциссу точки в которой касательная к графику функции парал-на оси ХСкачать

Решение задач

Выясните, какие из данных уравнений являются уравнениями окружности.

Найдите координаты центра и радиус каждой окружности.

а)

б)

в)

г) ;

д)

Рассмотрим каждое уравнение в отдельности.

а) – окружность,

б) – окружность,

в)
Выделим полный квадрат:

уравнение не является уравнением окружности.

г) .
Выделим полный квадрат:
– окружность,

д)
Выделим полный квадрат:
– окружность,

На окружности, заданной уравнением , найдите точки

а) с абсциссой –4; б) с ординатой 3.

Решение: построим окружность с центром (0;0) радиуса 5 (рис. 1).

Рис. 1. Иллюстрация к задаче

а) Координаты точек окружности с абсциссой –4 являются решениями системы:

Получаем точку и точку

Рис. 2. Иллюстрация к задаче

б) Координаты точек окружности с ординатой 3 являются решениями системы:

Рис. 3. Иллюстрация к задаче

Получаем точку и ту же самую точку

Ответ: .

Запишите уравнение окружности радиуса r с центром в точке А, если

а)

б)

в)

г)

а) Окружность
Ответ:

б) Окружность .
Ответ:

в) Окружность
Ответ:

г) Окружность
Ответ:

Напишите уравнение окружности с центром в начале координат, проходящей через точку

Рис. 4. Иллюстрация к задаче

Найдем радиус, как расстояние ОВ:

Запишем уравнение окружности с центром О(0;0):

Для контроля проверим, удовлетворяют ли полученному уравнению координаты точки В:

значит, точка В лежит на окружности.

Ответ:

Напишите уравнение окружности, проходящей через точку А(1;3), если известно, что центр окружности лежит на оси абсцисс, а радиус равен 5.

Сколько существует таких окружностей?

Дано: А(1;3) – точка окружности,

Найти: уравнение окружности (С; r=5).

Решение: центр искомой окружности удален от точки А(1;3) на расстояние 5, значит, он лежит на окружности с центром в точке А(1;3) радиуса 5, но он еще лежит и на оси Ох. Построим окружность (А(1;3); r=5) (рис. 5).