Ориентация векторов на плоскости (2 видео)

Ориентация плоскости и пространства

Базис (е_х,е₂) векторного пространства V₂ плоскости Е₂ называется правым, если кратчайший поровот от первого вектора е_х к вектору е₂ происходит против часовой стрелки.

Базис (е_1? е₂) векторного пространства И₂ плоскости Е₂ называется левым, если кратчайший поровот от первого вектора е_< к вектору е₂ происходит по часовой стрелке.

Все левые (правые) базисы составляют класс одноименных базисов.

Ориентацией векторного пространства называется класс одинаково ориентированных базисов. Выделяют один из классов и называют его положительным, а другой отрицательным. Обычно положительную ориентацию задают правым базисом (е₁₅ е₂), отрицательную — левым.

Векторное пространство V₂ называется ориентированным, если одна из ориентаций названа положительной, а другая — отрицательной.

Плоскость называется ориентированной, если ориентировано ее векторное пространство.

Замечание 1. Из приведенной теории следует, что для задания ориентации плоскости достаточно одно из направлений вращения назвать положительным, а другое — отрицательным. Обычно положительным считают то направление, которое противоположно направлению вращения часовой стрелки.

Замечание 2. Векторное пространство И₃ называется ориентированным, если одна из ориентаций названа положительной, а другая — отрицательной. Пространство называется ориентированным, если ориентировано его векторное пространство.

Обычно положительную ориентацию И₃ задают правой тройкой, отрицательную — левой тройкой.

Тройка (е_р е₂, е₃) называется правой (левой), если из конца третьего вектора кратчайший поворот от к е₂ происходит против часовой стрелки (по часовой стрелке).

задающих базис задающих базис

Содержание

Векторное произведение векторов
Угол между векторами. Ориентация пары векторов на плоскости или тройки векторов в пространстве.
Векторы на плоскости и в пространстве — основные определения
Определение вектора
Нулевой вектор
Длина вектора
Коллинеарность векторов
Направление векторов
Равные и противоположные векторы
Углы между векторами
📽️ Видео

Видео:Базис. Разложение вектора по базису.Скачать

Векторное произведение векторов

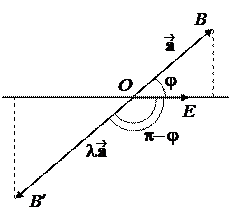
Пусть ориентация векторного пространства К₃ задана правой тройкой (z, j, :

Векторным произведением неколлинеарных векторов а и b , взятых в данном порядке, назовем вектор с, длина и направление которого определяются следующим образом: а) длина вектора | с 1=1 а || b | sin (р численно равна площади параллелограмма ОАВС (см. рис. а), б) вектор с перпендикулярен а и b , а ± с, b ± с; в) векторы а, Ь, с образуют базис, одноименный с базисом і, j, к .

Векторное произведение кол линеарных векторов а и b считается равным 0. Нуль-вектор считается коллинеарным любому вектору. Обозначение: с=1 a, b l = axb .

Видео:Ориентация векторов в пространстве. Правая и левая тройки векторовСкачать

Угол между векторами. Ориентация пары векторов на плоскости или тройки векторов в пространстве.

Определение. Пусть и – два ненулевых вектора. Отложим их из одной точки О: = , = . Тогда углом между векторами и называется угол между лучами OA и OB, т.е. a =ÐAOB. Пишем a =Ð( , ).

Если речь идет о векторах на плоскости, то можем ввести понятие ориентированного угла между векторами. Если кратчайший поворот

от луча OA к лучу OB осуществляется против часовой стрелки, то считаем, что a > 0, а если по часовой – то a 0 . Таким образом, – p a £ p . Если a > 0, то пара векторов (, ) называется правой, а если a 0 – то левой.

В пространстве понятие ориентированного угла не имеет смысла. Если посмотреть на плоскость, в которой лежат лучи OA и OB с одной стороны, то увидим, что кратчайший поворот от OA к OB осуществляется в одном направлении, а если посмотреть на плоскость с другой стороны, то мы увидим тот же поворот в другом направлении.

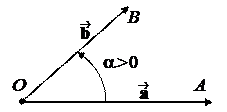
Пусть в пространстве даны три некомпланарных вектора , , . Отложим их из одной точки О: = , = , = . Тройка векторов (, , ) называется правой, если кратчайший поворот от луча OA к лучу OB, если смотреть из точки C , выглядит как осуществляющийся против часовой стрелки. Соответственно, если этот поворот выглядит как осуществляющийся по часовой стрелке, то тройка векторов (, , ) называется левой. На рисунке изображена правая тройка векторов.

Проекция вектора на ось.

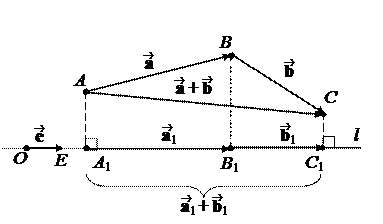
Пусть l – некоторая прямая в пространстве. Выберем точку OÎ l и единичный вектор ||l.Построим направленный отрезок = . Прямая l с отрезком называется осью. Иногда говорят, что ось – это прямая, на которой задано направление.

Определение. Пусть – произвольный вектор, а – произвольный направленный отрезок, который представляет . Опустим перпендикуляры AA₁ и BB₁ на прямую l. Пусть = . Тогда вектор

называется векторной проекцией вектора на ось l и обозначается p_l.

Мы имеем || . Поэтому согласно теореме 1 существует такое число p, что = p. Это число называется скалярной проекцией вектора на ось l . Поскольку –

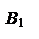
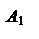
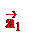
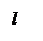
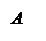
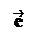
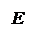
единичный вектор, то p – это длина вектора , если , и p = – ||, если ¯. Будем обозначать скалярную проекцию так: P_l.

Зная скалярную проекцию вектора мы можем найти его векторную проекцию:

Необходимо еще доказать, что определения скалярной и векторной проекции корректны, т.е. не зависят от выбора направленного отрезка , который представляет вектор . Другими словами, если мы отложим вектор от другой точки, то его скалярная и векторная проекции не изменятся,– и это надо доказать.

Проведем через точки A и B плоскости a и b перпендикулярно l. Тогда ½p½=½P_l½ есть расстояние между a и b .Выберем другой направленный отрезок , представляющий и проведем через точки A¢, B ¢ плоскости a¢ и b¢ перпендикулярно l. Направленные отрезки и эквивалентны, а значит, они совмещаются параллельным переносом. При этом переносе плоскость a совместится с a¢, а плоскость b – с b¢. Значит, расстояние между a¢ и b¢ равно расстоянию между a и b, и оно равно ½p½. Поэтому ½p½ не зависит от выбора направленного отрезка. Направление векторной проекции также не изменится при переносе, поэтому и знак p не изменится. Итак, скалярная проекция не зависит от выбора направленного отрезка, представляющего . В силу равенства (*) p_l также не зависит от выбора направленного отрезка.

Теорема 2. Свойства проекции вектора на ось.

1.P_l =| | cosÐ(, );

Доказательство. 1. Поскольку определение проекции не зависит от выбора точки A ,из которой отложен вектор , мы можем отложить его из точки О. Обозначим j =Ð(, ).

1 случай: j £ p/2. Тогда из DOBB₁ получим, что

2 случай: j > p/2. Тогда из DOBB₁ получим, что

2. Для скалярных проекций:

1 случай: l > 0. Тогда l и Ð(, l ) = j. Значит,

= l| |cos j = lP_l .

Ð(, l ) = p – j и cosÐ(,l ) = – cos j,

3случай: l = 0. Тогда равенство очевидно.

Для векторных проекций с помощью равенства (*) получаем:

3.Доказательство для векторных проекций показано на чертеже, но только для случая векторов на плоскости. Рисунок для векторов в пространстве можно найти в учебнике [10].

Для скалярных проекций равенство вытекает из равенства для векторных проекций. Например, в случае, изображенном на втором рисунке,

|A₁C₁|= |A₁B₁|+(– |B₁C₁|).

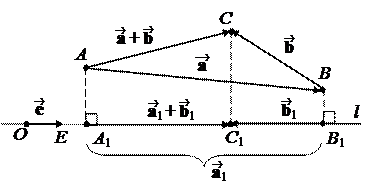
Видео:§11 Ориентация векторов в пространствеСкачать

Векторы на плоскости и в пространстве — основные определения

Видео:Геометрия. 9 класс. Векторы на плоскости /27.10.2020/Скачать

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a → . Если известны граничные точки вектора – его начало и конец, к примеру A и B , то вектор обозначается так A B → .

Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Видео:Геометрия. 9 класс. Векторы на плоскости /11.05.2021/Скачать

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Длину вектора A B → принято обозначать так A B → .

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Направление векторов

Сонаправленными векторами называют два коллинеарных вектора a → и b → , у которых направления совпадают, такие векторы обозначаются так a → ↑ ↑ b → .

Противоположно направленными векторами называются два коллинеарных вектора a → и b → , у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a → ↑ ↓ b → .

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Пусть заданы два произвольных вектора на плоскости или в пространстве a → и b → . Отложим от некоторой точки O плоскости или пространства векторы O A → = a → и O B → = b → . Лучи OA и OB образуют угол ∠ A O B = φ .

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).